人教版七年级数学下册5.1.2垂线 课件(19张ppt)
文档属性
| 名称 | 人教版七年级数学下册5.1.2垂线 课件(19张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 606.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
5.1.2
垂线
学习目标:
(1)理解垂线、垂线段的概念,会用三角尺或量角器过一点画已知直线的垂线.理解点到直线的距离的概念,能度量点到直线的距离.掌握垂线的性质.
(2)通过观察、思考、探究等活动归纳出垂线的概念和性质,并利用所学知识进行说理,体会从一般到特殊的方法,提高逻辑思维能力.通过利用垂线的性质解决简单的实际问题,提高应用意识.
学习重点:
垂线的概念和性质.
课件说明
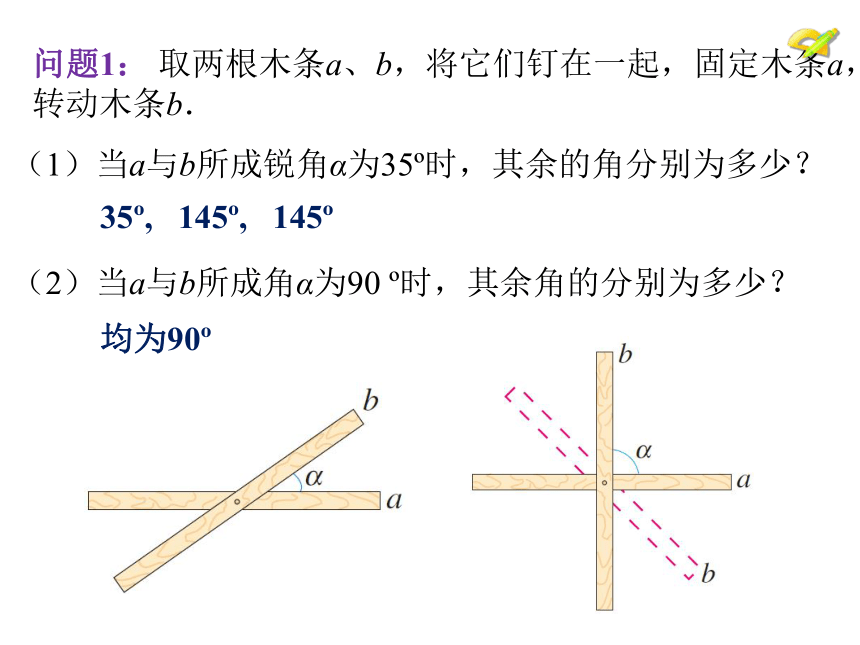
问题1:
取两根木条a、b,将它们钉在一起,固定木条a,转动木条b.
(2)当a与b所成角α为90
?时,其余角的分别为多少?
35?,
145?,
145?
均为90?
(1)当a与b所成锐角α为35?时,其余的角分别为多少?
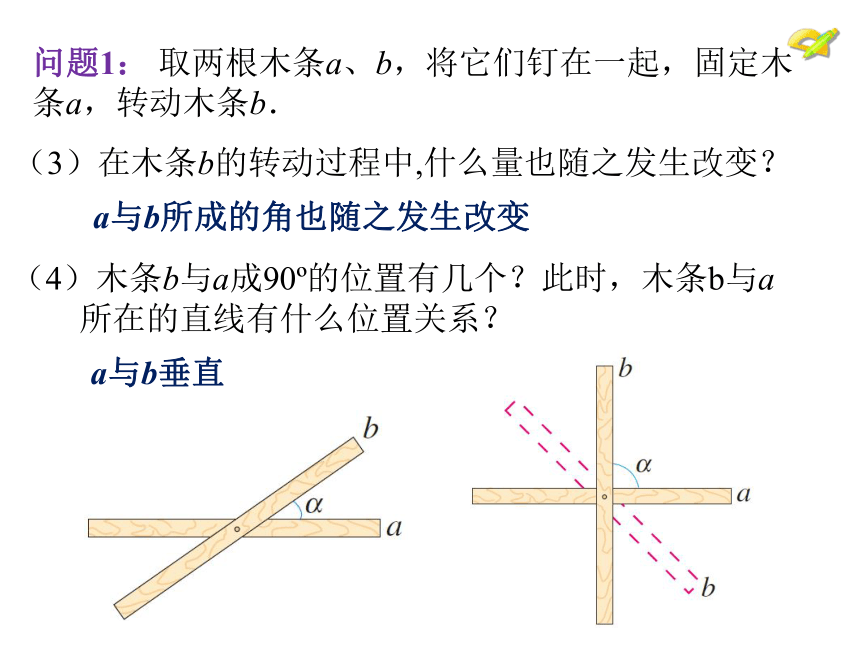
问题1:
取两根木条a、b,将它们钉在一起,固定木条a,转动木条b.
(3)在木条b的转动过程中,什么量也随之发生改变?
(4)木条b与a成90?的位置有几个?此时,木条b与a
所在的直线有什么位置关系?
a与b所成的角也随之发生改变
a与b垂直
(1)垂直概念:两条直线相交所成的四个角中,有一个角是直角时,叫做这两条直线互相垂直.两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
如图,AB
⊥CD,垂足为O.
记作:AB
⊥CD于点O.
(2)符号语言:
因为 AB
⊥CD,
所以 ∠AOC=90°.
反之,因为 ∠AOC=90°,
所以 AB⊥CD.
问题2:
(1)两条直线垂直和相交是什么关系?
(2)能否认为在同一平面内,两条直线的位置关系
有3种:相交,平行,垂直?
垂直是相交的特殊情况
不能,因为垂直是相交的特殊情况
问题2:
(3)如何判定两条射线垂直?两条线段呢?
(4)你能举出一些生活中与垂直有关的实例吗?
两条线段垂直、两条射线垂直、线段与射线垂直、线段与直线垂直、射线与直线垂直,都是指它们所在的直线垂直.
问题3:用三角尺或量角器画已知直线l的垂线.
(1)用三角尺或量角器画已知直线l的垂线,这样的垂线能画出几条?
无数条
问题3:用三角尺或量角器画已知直线l的垂线
(1)用三角尺或量角器画已知直线l的垂线,这样的垂线能画出几条?
(2)经过一点画已知直线l的垂线,这样的垂线能画出几条?
①经过一点画已知直线l的垂线有几种情况?
②通过画图,你发现过一个点可以画几条直线与已知直线垂直?
垂线性质1:在同一平面内,过一点有且只有一条直线与已知直线垂直.
练习:1.过点P画出射线AB或线段AB的垂线.
练习:
2.请同学们在一张半透明的纸上画一条直线l,在l上任取一点P,在l外任取一点Q,分别折出过点P,Q且与l垂直的直线.
(1)为什么你折出的折痕是l的垂线?
(2)过点P或过点Q,你们分别折出几条直线与l垂直?
问题5:在灌溉时,要把河中的水引到农田P处,如何挖掘能使渠道最短?
思考:
(1)你能将这个实际问题转化成数学问题吗?
(2)在直线上有无数个点,试着取几个点与点P相连,比较一下它们的大小关系.你有什么发现?
(3)你能猜想一下最短的位置会在哪儿?它唯一吗?为什么?
(4)你能用一句话总结出观察得出的结论吗?
垂线性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
点到直线的距离:直线外一点到这条直线的垂线段的长度,叫点到直线的距离.
思考:
(5)如果图中的比例尺为1:1000000,水渠大概要挖多长?
(6)你能列举生活中类似的实例吗?
归纳小结
1.什么是垂直?垂直和相交有什么关系?我们是如何刻画两直线垂直的位置关系的?
2.垂线有哪些性质?
布置作业
教科书
习题5.1
第3、4、5、6、7题
5.1.2
垂线
学习目标:
(1)理解垂线、垂线段的概念,会用三角尺或量角器过一点画已知直线的垂线.理解点到直线的距离的概念,能度量点到直线的距离.掌握垂线的性质.
(2)通过观察、思考、探究等活动归纳出垂线的概念和性质,并利用所学知识进行说理,体会从一般到特殊的方法,提高逻辑思维能力.通过利用垂线的性质解决简单的实际问题,提高应用意识.
学习重点:
垂线的概念和性质.
课件说明
问题1:
取两根木条a、b,将它们钉在一起,固定木条a,转动木条b.
(2)当a与b所成角α为90
?时,其余角的分别为多少?
35?,
145?,
145?
均为90?
(1)当a与b所成锐角α为35?时,其余的角分别为多少?
问题1:
取两根木条a、b,将它们钉在一起,固定木条a,转动木条b.
(3)在木条b的转动过程中,什么量也随之发生改变?
(4)木条b与a成90?的位置有几个?此时,木条b与a
所在的直线有什么位置关系?
a与b所成的角也随之发生改变
a与b垂直
(1)垂直概念:两条直线相交所成的四个角中,有一个角是直角时,叫做这两条直线互相垂直.两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
如图,AB
⊥CD,垂足为O.
记作:AB
⊥CD于点O.
(2)符号语言:
因为 AB
⊥CD,
所以 ∠AOC=90°.
反之,因为 ∠AOC=90°,
所以 AB⊥CD.
问题2:
(1)两条直线垂直和相交是什么关系?
(2)能否认为在同一平面内,两条直线的位置关系
有3种:相交,平行,垂直?
垂直是相交的特殊情况
不能,因为垂直是相交的特殊情况
问题2:
(3)如何判定两条射线垂直?两条线段呢?
(4)你能举出一些生活中与垂直有关的实例吗?
两条线段垂直、两条射线垂直、线段与射线垂直、线段与直线垂直、射线与直线垂直,都是指它们所在的直线垂直.
问题3:用三角尺或量角器画已知直线l的垂线.
(1)用三角尺或量角器画已知直线l的垂线,这样的垂线能画出几条?
无数条
问题3:用三角尺或量角器画已知直线l的垂线
(1)用三角尺或量角器画已知直线l的垂线,这样的垂线能画出几条?
(2)经过一点画已知直线l的垂线,这样的垂线能画出几条?
①经过一点画已知直线l的垂线有几种情况?
②通过画图,你发现过一个点可以画几条直线与已知直线垂直?
垂线性质1:在同一平面内,过一点有且只有一条直线与已知直线垂直.
练习:1.过点P画出射线AB或线段AB的垂线.
练习:
2.请同学们在一张半透明的纸上画一条直线l,在l上任取一点P,在l外任取一点Q,分别折出过点P,Q且与l垂直的直线.
(1)为什么你折出的折痕是l的垂线?
(2)过点P或过点Q,你们分别折出几条直线与l垂直?
问题5:在灌溉时,要把河中的水引到农田P处,如何挖掘能使渠道最短?
思考:
(1)你能将这个实际问题转化成数学问题吗?
(2)在直线上有无数个点,试着取几个点与点P相连,比较一下它们的大小关系.你有什么发现?
(3)你能猜想一下最短的位置会在哪儿?它唯一吗?为什么?
(4)你能用一句话总结出观察得出的结论吗?
垂线性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
点到直线的距离:直线外一点到这条直线的垂线段的长度,叫点到直线的距离.
思考:
(5)如果图中的比例尺为1:1000000,水渠大概要挖多长?
(6)你能列举生活中类似的实例吗?
归纳小结
1.什么是垂直?垂直和相交有什么关系?我们是如何刻画两直线垂直的位置关系的?
2.垂线有哪些性质?
布置作业
教科书
习题5.1
第3、4、5、6、7题
