甘肃省平凉市庄浪四中2020-2021学年高二下学期开学考试数学(理)试题 Word版缺答案
文档属性
| 名称 | 甘肃省平凉市庄浪四中2020-2021学年高二下学期开学考试数学(理)试题 Word版缺答案 | 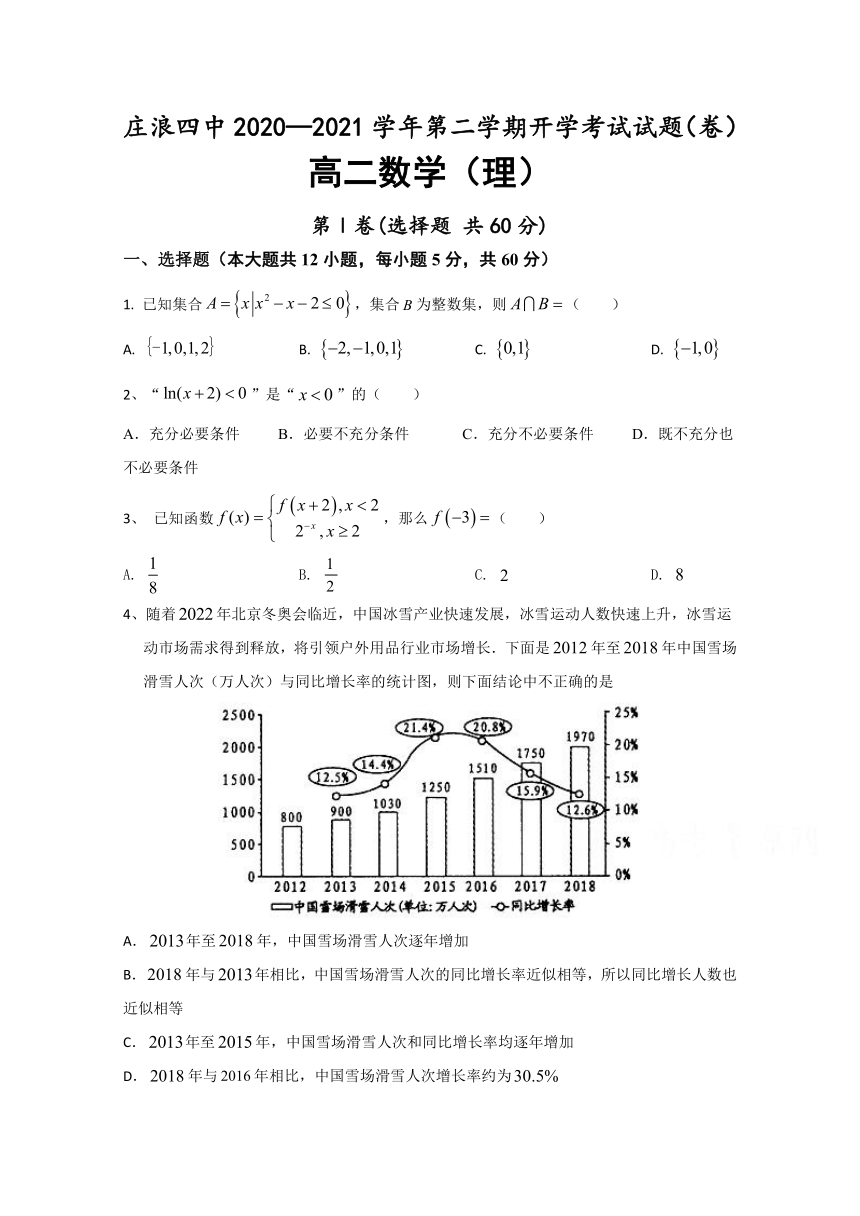 | |
| 格式 | doc | ||
| 文件大小 | 495.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 09:07:58 | ||
图片预览


文档简介
庄浪四中2020—2021学年第二学期开学考试试题(卷)
高二数学(理)
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,共60分)
1. 已知集合,集合为整数集,则( )
A. B. C. D.
2、“”是“”的( )
A.充分必要条件 B.必要不充分条件 C.充分不必要条件 D.既不充分也不必要条件
3、 已知函数,那么( )
A. B. C. D.
4、随着年北京冬奥会临近,中国冰雪产业快速发展,冰雪运动人数快速上升,冰雪运动市场需求得到释放,将引领户外用品行业市场增长.下面是年至年中国雪场滑雪人次(万人次)与同比增长率的统计图,则下面结论中不正确的是
A.年至年,中国雪场滑雪人次逐年增加
B.年与年相比,中国雪场滑雪人次的同比增长率近似相等,所以同比增长人数也近似相等
C.年至年,中国雪场滑雪人次和同比增长率均逐年增加
D.年与年相比,中国雪场滑雪人次增长率约为
5、设变量、满足约束条件,则目标函数的最小值为( )
A.2 B.3 C.4 D.9
6、唐朝的狩猎景象浮雕银杯如图1所示.其浮雕临摹了国画、漆绘和墓室壁画,体现了古人的智慧与工艺.它的盛酒部分可以近似地看作是半球与圆柱的组合体(假设内壁表面光滑,忽略杯壁厚度),如图2所示.已知球的半径为R,酒杯内壁表面积为,设酒杯上部分(圆柱)的体积为,下部分(半球)的体积为,则( )
A. B.1 C. D.2、
7、如图,在平行六面体中,若 则下列向量中与相等的是( )
A. B. C. D.
8、已知平面向量,均为单位向量,若向量,的夹角为,则( )
A. 25 B. 7 C. 5 D.
9、 已知等差数列满足,,则它的前10项的和( )
A. 138 B. 135 C. 95 D. 23
10、已知P为椭圆上的一个点,点M,N分别为圆(x+3)2+y2=1和圆(x-3)2+y2=4上的动点,则|PM|+|PN|的最小值为( )
A.6 B.7 C.10 D.13
11、已知函数(,),若函数在区间内没有零点,则的取值范围是( )
A. B. C. D.
12、已知点是双曲线右焦点,点是该双曲线的左顶点,过且垂直于轴的直线与双曲线交于两点,若是钝角,则该双曲线的离心率的取值范围是 ( )
A. B. C. D.
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题5分,共20分)
13、若抛物线上一点到其准线的距离为,则抛物线的标准方程是
14、已知中,内角,,所对边长分别为,,,若,,,则的面积等于________.
15、已知正数x、y的等差中项为1,则的最小值__________.
16、已知函数,,若存在,,,使得成立,则实数的取值范围是 .
三、解答题(本大题共6小题,共70分)
17、(本小题满分10分)已知命题不等式的解集是. 命题函数在定义域内是增函数.若“”为真命题,“”为假命题,求实数的取值范围.
18、(本小题满分12分)设等差数列{an}的前n项和为Sn,S7=14,a2+a12=10.
(Ⅰ)求an;
(Ⅱ)设,证明:数列{bn}是等比数列,并求其前n项和Tn.
19、(本小题满分12分)某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本数据(xi,yi)(i=1,2,…,20),其中xi和yi分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得
,,,,.
(Ⅰ)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
(Ⅱ)求样本(xi,yi)(i=1,2,…,20)的相关系数(精确到0.01);
(Ⅲ)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.
附:相关系数r=,≈1.414.
20、(本小题满分12分)的内角的对边分别为,已知.
(Ⅰ)求角的大小;
(Ⅱ)若,求.
21、(本小题满分12分)如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=PD.
(Ⅰ)证明:平面PQC⊥平面DCQ ; (Ⅱ)求二面角Q—BP—C的余弦值。
22、(本小题满分12分)过点的椭圆的离心率为,椭圆与轴交于两点、,过点C的直线l与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q.
(Ⅰ)求椭圆的方程 ;
(Ⅱ)当直线l过椭圆右焦点时,求线段CD的长;
(Ⅲ)当点P异于点B时,求证:为定值.
高二数学(理)
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,共60分)
1. 已知集合,集合为整数集,则( )
A. B. C. D.
2、“”是“”的( )
A.充分必要条件 B.必要不充分条件 C.充分不必要条件 D.既不充分也不必要条件
3、 已知函数,那么( )
A. B. C. D.
4、随着年北京冬奥会临近,中国冰雪产业快速发展,冰雪运动人数快速上升,冰雪运动市场需求得到释放,将引领户外用品行业市场增长.下面是年至年中国雪场滑雪人次(万人次)与同比增长率的统计图,则下面结论中不正确的是
A.年至年,中国雪场滑雪人次逐年增加
B.年与年相比,中国雪场滑雪人次的同比增长率近似相等,所以同比增长人数也近似相等
C.年至年,中国雪场滑雪人次和同比增长率均逐年增加
D.年与年相比,中国雪场滑雪人次增长率约为
5、设变量、满足约束条件,则目标函数的最小值为( )
A.2 B.3 C.4 D.9
6、唐朝的狩猎景象浮雕银杯如图1所示.其浮雕临摹了国画、漆绘和墓室壁画,体现了古人的智慧与工艺.它的盛酒部分可以近似地看作是半球与圆柱的组合体(假设内壁表面光滑,忽略杯壁厚度),如图2所示.已知球的半径为R,酒杯内壁表面积为,设酒杯上部分(圆柱)的体积为,下部分(半球)的体积为,则( )
A. B.1 C. D.2、
7、如图,在平行六面体中,若 则下列向量中与相等的是( )
A. B. C. D.
8、已知平面向量,均为单位向量,若向量,的夹角为,则( )
A. 25 B. 7 C. 5 D.
9、 已知等差数列满足,,则它的前10项的和( )
A. 138 B. 135 C. 95 D. 23
10、已知P为椭圆上的一个点,点M,N分别为圆(x+3)2+y2=1和圆(x-3)2+y2=4上的动点,则|PM|+|PN|的最小值为( )
A.6 B.7 C.10 D.13
11、已知函数(,),若函数在区间内没有零点,则的取值范围是( )
A. B. C. D.
12、已知点是双曲线右焦点,点是该双曲线的左顶点,过且垂直于轴的直线与双曲线交于两点,若是钝角,则该双曲线的离心率的取值范围是 ( )
A. B. C. D.
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题5分,共20分)
13、若抛物线上一点到其准线的距离为,则抛物线的标准方程是
14、已知中,内角,,所对边长分别为,,,若,,,则的面积等于________.
15、已知正数x、y的等差中项为1,则的最小值__________.
16、已知函数,,若存在,,,使得成立,则实数的取值范围是 .
三、解答题(本大题共6小题,共70分)
17、(本小题满分10分)已知命题不等式的解集是. 命题函数在定义域内是增函数.若“”为真命题,“”为假命题,求实数的取值范围.
18、(本小题满分12分)设等差数列{an}的前n项和为Sn,S7=14,a2+a12=10.
(Ⅰ)求an;
(Ⅱ)设,证明:数列{bn}是等比数列,并求其前n项和Tn.
19、(本小题满分12分)某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本数据(xi,yi)(i=1,2,…,20),其中xi和yi分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得
,,,,.
(Ⅰ)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
(Ⅱ)求样本(xi,yi)(i=1,2,…,20)的相关系数(精确到0.01);
(Ⅲ)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.
附:相关系数r=,≈1.414.
20、(本小题满分12分)的内角的对边分别为,已知.
(Ⅰ)求角的大小;
(Ⅱ)若,求.
21、(本小题满分12分)如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=PD.
(Ⅰ)证明:平面PQC⊥平面DCQ ; (Ⅱ)求二面角Q—BP—C的余弦值。
22、(本小题满分12分)过点的椭圆的离心率为,椭圆与轴交于两点、,过点C的直线l与椭圆交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q.
(Ⅰ)求椭圆的方程 ;
(Ⅱ)当直线l过椭圆右焦点时,求线段CD的长;
(Ⅲ)当点P异于点B时,求证:为定值.
同课章节目录
