六年级下册数学课件 圆柱与圆锥 第6课时 圆柱的体积(2)(共25张PPT)人教版
文档属性
| 名称 | 六年级下册数学课件 圆柱与圆锥 第6课时 圆柱的体积(2)(共25张PPT)人教版 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 11:07:40 | ||
图片预览







文档简介
第三单元 圆柱与圆锥
第6课时 圆柱的体积(2)
六年级数学下册(RJ)教学课件
目录
CONTENTS
情景导入
01
学习目标
02
探究与发现
03
学以致用
04
课后作业
06
课堂小结
05
情景导学
第一部分
情景导学
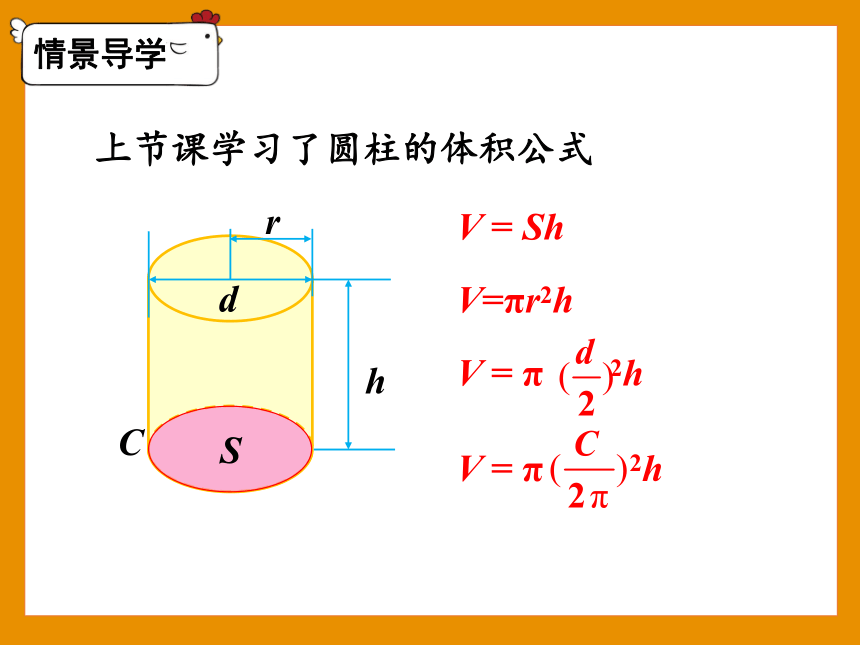
r
h
V=πr2h
上节课学习了圆柱的体积公式
S
C
d
V = Sh
V = π 2h
V = π 2h
情景导学
1.一个圆柱底面积4.5平方米,高3米。求它的体积。
4.5×3=13.5(立方米)
2.一个圆柱底面半径3厘米,高4厘米。求它的体积。
3.14×32×4=113.04(立方厘米)
算一算
情景导学
算一算
3.一个圆柱底面直径6分米,高8分米。求它的体积。
3.14×(6÷2)2×8=226.08(立方分米)
4.一个圆柱底面周长12.56厘米,高6厘米。求它的体积。
3.14×(12.56÷3.14÷2)2×6
=75.36(立方厘米)
第二部分
学习目标
学习目标
能应用圆柱的体积公式解决一些实际问题。
第三部分
探究与发现
探索与发现
要回答这个问题,先要计算出什么?
杯子的容积
容积的计算方法与体积的计算方法相同
下图中的杯子能不能装下这袋牛奶?(数据是从杯子里面测量得到的。)
探索与发现
杯子的容积:
50.24×10
=502.4(cm?)
=502.4(mL)
答:因为502.4大于498,所以杯子能装下这袋牛奶。
杯子的底面积:
3.14×(8÷2)?
=3.14×4?
=3.14×16
=50.24(cm?)
第四部分
学以致用
学以致用
小明和妈妈出去游玩,带了一个圆柱形保温杯,从里面量底面直径是8cm,高是15cm。如果两人游玩期间要喝1L水,带这杯水够喝吗?
保温杯的底面积:3.14×(8÷2)2
= 3.14×42
= 3.14×16
= 50.24 (cm2)
保温杯的容积:50.24×15
=753.6 (cm?)
=0.7536(L)
0.7536<1
答:所以带这杯水不够喝。
学以致用
3.14×(0.4÷2)2×5=0.628(m3)
0.628÷0.02=31.4≈31(张)
答:这根木料最多能做31张课桌。
一根圆柱形木料底面直径是0.4m,长5m。如果做一张课桌用去木料0.02m3。这根木料最多能做多少张课桌?
学以致用
求下面图形的表面积和体积。(单位:cm)
体积:
3.14×(6÷2)2×12=339.12(cm3)
表面积:
3.14×6×12+3.14×(6÷2)2×2
=282.6(cm2)
学以致用
体积:
15×10×20=3000(cm3)
表面积:
(15×10+15×20+10×20)×2
=1300(cm2)
求下面图形的表面积和体积。(单位:cm)
学以致用
求下面图形的表面积和体积。(单位:cm)
体积:
3.14×(14÷2)2×5
= 769.3 (cm3)
表面积:
3.14×(14÷2)2×2+3.14×14×5
=527.52(cm2)
学以致用
明明家里来了两位小客人,妈妈冲了1L果汁。如果用右图中的玻璃杯喝果汁,够明明和客人每人一杯吗?
3.14×(6÷2)2×11=310.86(mL)
1L=1000mL
1000÷310.86≈3.22
3.22>3
答:够明明和客人每人一杯。
一种电热水炉的水龙头的内直径是1.2cm,打开水龙头后水的流速是20厘米/秒,一个容积为1L的保温壶,50秒能装满水吗?
学以致用
3.14×(1.2÷2)2×20×50=1130.4(cm3)
1130.4cm3>1000cm3=1L
答: 50秒能装满水。
学以致用
*右面这个长方形的长是20cm,宽是10cm。分别以长和宽为轴旋转一周,得到两个元柱体。它们的体积各是多少?
以长为轴旋转一周的体积
3.14×102×20=6280(cm3)
以宽为轴旋转一周的体积
3.14×202×10=12560(cm3)
学以致用
第一个
3.14×(18÷3.14÷2)2×2≈51.59(dm3)
或3.14×(2÷3.14÷2)2×18≈5.73(dm3)
第二个
3.14×(12÷3.14÷2)2×3≈34.39(dm3)
或3.14×(3÷3.14÷2)2×12≈8.60(dm3)
*下面4个图形的面积都是36dm2。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?有什么发现?(单位:dm)
学以致用
第三个
3.14×(9÷3.14÷2)2×4≈25.80(dm3)
或3.14×(4÷3.14÷2)2×9≈11.46(dm3)
第四个
3.14×(6÷3.14÷2)2×3≈8.60(dm3)
*下面4个图形的面积都是36dm2。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?有什么发现?(单位:dm)
答:以18为周长,2为高的圆柱体体积最大,以2为周长,18为高的圆柱体体积最小。
第五部分
课堂小结
知识小结
求圆柱形容器的容积的计算方法与圆柱体积计算方法相同,注意所需数据应从容器的里面测量得到。
谢谢观看
下课!
第6课时 圆柱的体积(2)
六年级数学下册(RJ)教学课件
目录
CONTENTS
情景导入
01
学习目标
02
探究与发现
03
学以致用
04
课后作业
06
课堂小结
05
情景导学
第一部分
情景导学
r
h
V=πr2h
上节课学习了圆柱的体积公式
S
C
d
V = Sh
V = π 2h
V = π 2h
情景导学
1.一个圆柱底面积4.5平方米,高3米。求它的体积。
4.5×3=13.5(立方米)
2.一个圆柱底面半径3厘米,高4厘米。求它的体积。
3.14×32×4=113.04(立方厘米)
算一算
情景导学
算一算
3.一个圆柱底面直径6分米,高8分米。求它的体积。
3.14×(6÷2)2×8=226.08(立方分米)
4.一个圆柱底面周长12.56厘米,高6厘米。求它的体积。
3.14×(12.56÷3.14÷2)2×6
=75.36(立方厘米)
第二部分
学习目标
学习目标
能应用圆柱的体积公式解决一些实际问题。
第三部分
探究与发现
探索与发现
要回答这个问题,先要计算出什么?
杯子的容积
容积的计算方法与体积的计算方法相同
下图中的杯子能不能装下这袋牛奶?(数据是从杯子里面测量得到的。)
探索与发现
杯子的容积:
50.24×10
=502.4(cm?)
=502.4(mL)
答:因为502.4大于498,所以杯子能装下这袋牛奶。
杯子的底面积:
3.14×(8÷2)?
=3.14×4?
=3.14×16
=50.24(cm?)
第四部分
学以致用
学以致用
小明和妈妈出去游玩,带了一个圆柱形保温杯,从里面量底面直径是8cm,高是15cm。如果两人游玩期间要喝1L水,带这杯水够喝吗?
保温杯的底面积:3.14×(8÷2)2
= 3.14×42
= 3.14×16
= 50.24 (cm2)
保温杯的容积:50.24×15
=753.6 (cm?)
=0.7536(L)
0.7536<1
答:所以带这杯水不够喝。
学以致用
3.14×(0.4÷2)2×5=0.628(m3)
0.628÷0.02=31.4≈31(张)
答:这根木料最多能做31张课桌。
一根圆柱形木料底面直径是0.4m,长5m。如果做一张课桌用去木料0.02m3。这根木料最多能做多少张课桌?
学以致用
求下面图形的表面积和体积。(单位:cm)
体积:
3.14×(6÷2)2×12=339.12(cm3)
表面积:
3.14×6×12+3.14×(6÷2)2×2
=282.6(cm2)
学以致用
体积:
15×10×20=3000(cm3)
表面积:
(15×10+15×20+10×20)×2
=1300(cm2)
求下面图形的表面积和体积。(单位:cm)
学以致用
求下面图形的表面积和体积。(单位:cm)
体积:
3.14×(14÷2)2×5
= 769.3 (cm3)
表面积:
3.14×(14÷2)2×2+3.14×14×5
=527.52(cm2)
学以致用
明明家里来了两位小客人,妈妈冲了1L果汁。如果用右图中的玻璃杯喝果汁,够明明和客人每人一杯吗?
3.14×(6÷2)2×11=310.86(mL)
1L=1000mL
1000÷310.86≈3.22
3.22>3
答:够明明和客人每人一杯。
一种电热水炉的水龙头的内直径是1.2cm,打开水龙头后水的流速是20厘米/秒,一个容积为1L的保温壶,50秒能装满水吗?
学以致用
3.14×(1.2÷2)2×20×50=1130.4(cm3)
1130.4cm3>1000cm3=1L
答: 50秒能装满水。
学以致用
*右面这个长方形的长是20cm,宽是10cm。分别以长和宽为轴旋转一周,得到两个元柱体。它们的体积各是多少?
以长为轴旋转一周的体积
3.14×102×20=6280(cm3)
以宽为轴旋转一周的体积
3.14×202×10=12560(cm3)
学以致用
第一个
3.14×(18÷3.14÷2)2×2≈51.59(dm3)
或3.14×(2÷3.14÷2)2×18≈5.73(dm3)
第二个
3.14×(12÷3.14÷2)2×3≈34.39(dm3)
或3.14×(3÷3.14÷2)2×12≈8.60(dm3)
*下面4个图形的面积都是36dm2。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?有什么发现?(单位:dm)
学以致用
第三个
3.14×(9÷3.14÷2)2×4≈25.80(dm3)
或3.14×(4÷3.14÷2)2×9≈11.46(dm3)
第四个
3.14×(6÷3.14÷2)2×3≈8.60(dm3)
*下面4个图形的面积都是36dm2。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?有什么发现?(单位:dm)
答:以18为周长,2为高的圆柱体体积最大,以2为周长,18为高的圆柱体体积最小。
第五部分
课堂小结
知识小结
求圆柱形容器的容积的计算方法与圆柱体积计算方法相同,注意所需数据应从容器的里面测量得到。
谢谢观看
下课!
