六年级下册数学人教版课件 整理与复习 图形与几何 第4课时 立体图形的认识与测量(2)(共27张PPT)
文档属性
| 名称 | 六年级下册数学人教版课件 整理与复习 图形与几何 第4课时 立体图形的认识与测量(2)(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 13:27:57 | ||
图片预览






文档简介
(共27张PPT)
第六单元 整理与复习
第4课时 立体图形的认识与测量(2)
六年级数学下册(RJ)教学课件
2.图形与几何
目录
CONTENTS
情景导入
01
学习目标
02
探究与发现
03
学以致用
04
课后作业
06
课堂小结
05
情景导学
第一部分
情景导学
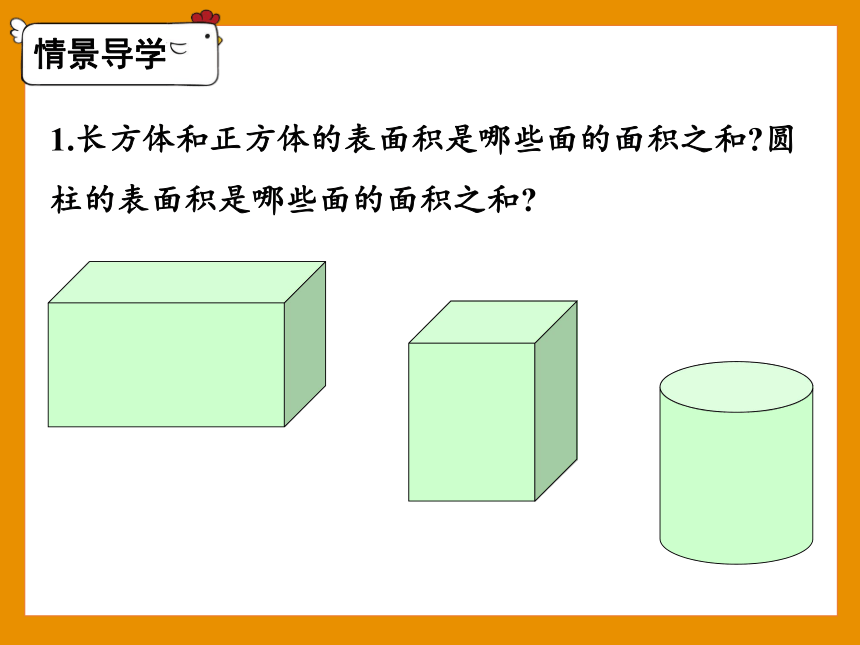
1.长方体和正方体的表面积是哪些面的面积之和 圆柱的表面积是哪些面的面积之和
情景导学
2.圆柱的侧面沿高展开是什么形状 侧面展开的长方形的长、宽与圆柱有什么关系 圆柱的侧面积怎样计算
情景导学
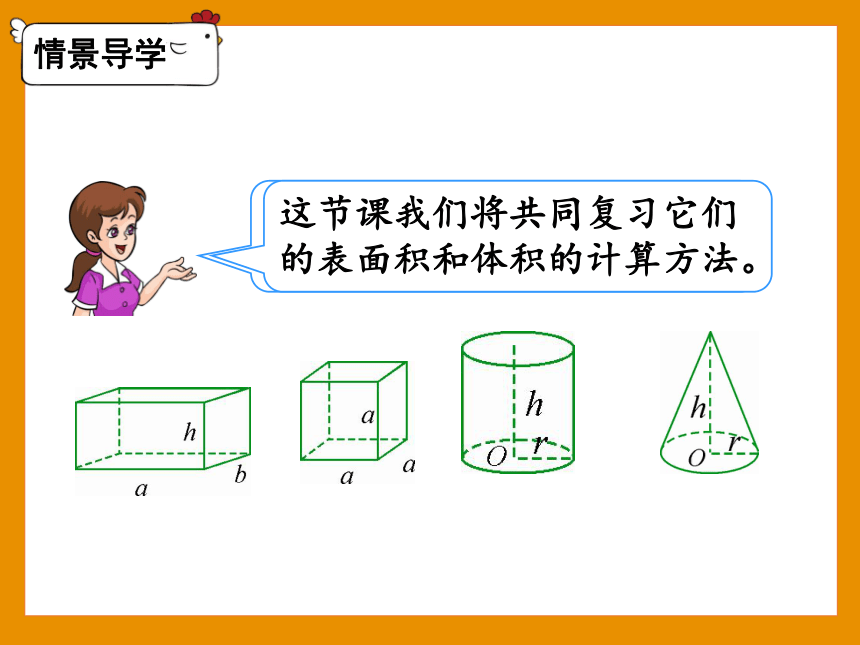
上节课我们回顾了长方体、正方体、圆柱、圆锥的特征。
这节课我们将共同复习它们的表面积和体积的计算方法。
第二部分
学习目标
学习目标
掌握所学立体图形表面积、体积的计算方法,能运用立体图形的相关知识解决实际问题。
第三部分
探究与发现
探索与发现
什么是立体图形的表面积 什么是立体图形的体积
表面积、体积的定义
表面积:一个立体图形所有面的面积总和。
体积:物体所占空间的大小。
1
探索与发现
立体图形 表面积计算公式 体积计算公式
S=2(ah+bh+ab) V=abh V=底面积×高
S=6a2 V=a3
表面积、体积的计算
S=2πr2+2πrh
V=πr2h
V= πr2h
1
3
2
探索与发现
长方体、正方体与圆柱的体积计算公式有什么联系
因为它们都是直柱体,所以都可以用底面积×高来计算。
探索与发现
等底等高的圆柱和圆锥的体积有什么关系
问题
等底等高的圆柱体积是圆锥体积的3倍。
他说的对吗
探索与发现
不规则物体体积的计算
将一块石头放进装有水的圆柱形容器里,你们发现了什么
水面高度升高了,因为石头占了圆柱体容器中水的空间。
你能根据这个现象求出石头的体积吗?
从中联想到了其他不规则物体体积的求法吗
3
排水法
探索与发现
容积的计算方法及注意事项
计算容积与计算体积的方法相同吗
相同。
有什么要注意的地方吗
要注意应从里面量容器的相关数据
4
探索与发现
复习立体图形的展开图
立体图形
平面图形
折叠
展开
怎样将一个立体图形的展开图进行还原
我们以正方体为例。
5
探索与发现
第四部分
学以致用
学以致用
把一个底面直径是2m,高是3m的圆柱沿底面直径切成两半,表面积增加了( )m2;沿横截面切成两半,表面积增加了( )m2。
答案:2×3×2=12m2
3.14×(2÷2)2×2=6.28m2
学以致用
(1)一个直角三角形,绕它的一条直角边旋转一周,能形成一个圆锥。 ( )
(2)把一段圆柱形木材削成一个最大的圆锥,削去的部分是原来的2/3。 ( )
(3)圆柱的底面半径扩大为原来的两倍,高不变,它的体积也扩大为原来的两倍。 ( )
(4)圆锥的体积等于圆柱体积的1/3。 ( )
√
√
×
×
判断。
学以致用
练习十八习题
(1)F
(2)E
(3)量出A面的长和宽,B面的长(合理即可)
学以致用
11.把一个棱长6cm的正方体切成棱长2cm的小正方体,可以得到多少个小正方体 它们的表面积之和比原来大正方形的表面积增加了多少
V大正方体=63=216(cm3)
V小正方体=23=8(cm3)
216÷8=27(个)
S大正方体=6×62=216(cm2)
S小正方体=6×22=24(cm2)
24×27-216=432(cm2)
学以致用
12.把一块棱长10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥形铁块的高约是多少 (得数保留整厘米。)
学以致用
14.这只工具箱的下半部是棱长为20cm的正方体,上半部是圆柱的一半。算出它的表面积和体积。
第五部分
课堂小结
知识小结
谢谢观看
下课!
第六单元 整理与复习
第4课时 立体图形的认识与测量(2)
六年级数学下册(RJ)教学课件
2.图形与几何
目录
CONTENTS
情景导入
01
学习目标
02
探究与发现
03
学以致用
04
课后作业
06
课堂小结
05
情景导学
第一部分
情景导学
1.长方体和正方体的表面积是哪些面的面积之和 圆柱的表面积是哪些面的面积之和
情景导学
2.圆柱的侧面沿高展开是什么形状 侧面展开的长方形的长、宽与圆柱有什么关系 圆柱的侧面积怎样计算
情景导学
上节课我们回顾了长方体、正方体、圆柱、圆锥的特征。
这节课我们将共同复习它们的表面积和体积的计算方法。
第二部分
学习目标
学习目标
掌握所学立体图形表面积、体积的计算方法,能运用立体图形的相关知识解决实际问题。
第三部分
探究与发现
探索与发现
什么是立体图形的表面积 什么是立体图形的体积
表面积、体积的定义
表面积:一个立体图形所有面的面积总和。
体积:物体所占空间的大小。
1
探索与发现
立体图形 表面积计算公式 体积计算公式
S=2(ah+bh+ab) V=abh V=底面积×高
S=6a2 V=a3
表面积、体积的计算
S=2πr2+2πrh
V=πr2h
V= πr2h
1
3
2
探索与发现
长方体、正方体与圆柱的体积计算公式有什么联系
因为它们都是直柱体,所以都可以用底面积×高来计算。
探索与发现
等底等高的圆柱和圆锥的体积有什么关系
问题
等底等高的圆柱体积是圆锥体积的3倍。
他说的对吗
探索与发现
不规则物体体积的计算
将一块石头放进装有水的圆柱形容器里,你们发现了什么
水面高度升高了,因为石头占了圆柱体容器中水的空间。
你能根据这个现象求出石头的体积吗?
从中联想到了其他不规则物体体积的求法吗
3
排水法
探索与发现
容积的计算方法及注意事项
计算容积与计算体积的方法相同吗
相同。
有什么要注意的地方吗
要注意应从里面量容器的相关数据
4
探索与发现
复习立体图形的展开图
立体图形
平面图形
折叠
展开
怎样将一个立体图形的展开图进行还原
我们以正方体为例。
5
探索与发现
第四部分
学以致用
学以致用
把一个底面直径是2m,高是3m的圆柱沿底面直径切成两半,表面积增加了( )m2;沿横截面切成两半,表面积增加了( )m2。
答案:2×3×2=12m2
3.14×(2÷2)2×2=6.28m2
学以致用
(1)一个直角三角形,绕它的一条直角边旋转一周,能形成一个圆锥。 ( )
(2)把一段圆柱形木材削成一个最大的圆锥,削去的部分是原来的2/3。 ( )
(3)圆柱的底面半径扩大为原来的两倍,高不变,它的体积也扩大为原来的两倍。 ( )
(4)圆锥的体积等于圆柱体积的1/3。 ( )
√
√
×
×
判断。
学以致用
练习十八习题
(1)F
(2)E
(3)量出A面的长和宽,B面的长(合理即可)
学以致用
11.把一个棱长6cm的正方体切成棱长2cm的小正方体,可以得到多少个小正方体 它们的表面积之和比原来大正方形的表面积增加了多少
V大正方体=63=216(cm3)
V小正方体=23=8(cm3)
216÷8=27(个)
S大正方体=6×62=216(cm2)
S小正方体=6×22=24(cm2)
24×27-216=432(cm2)
学以致用
12.把一块棱长10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥形铁块的高约是多少 (得数保留整厘米。)
学以致用
14.这只工具箱的下半部是棱长为20cm的正方体,上半部是圆柱的一半。算出它的表面积和体积。
第五部分
课堂小结
知识小结
谢谢观看
下课!
