2021年甘肃省张掖市甘州区甘州中学九年级数学下册开学考试卷(Word版含答案)
文档属性
| 名称 | 2021年甘肃省张掖市甘州区甘州中学九年级数学下册开学考试卷(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 282.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 00:00:00 | ||
图片预览




文档简介
张掖市甘州中学九年级下册开学考试卷
一.选择题
1.若反比例函数的图象经过(﹣1,3),则这个函数的图象一定过( )
A.(﹣3,1) B.(﹣,3) C.(﹣3,﹣1) D.(,3)
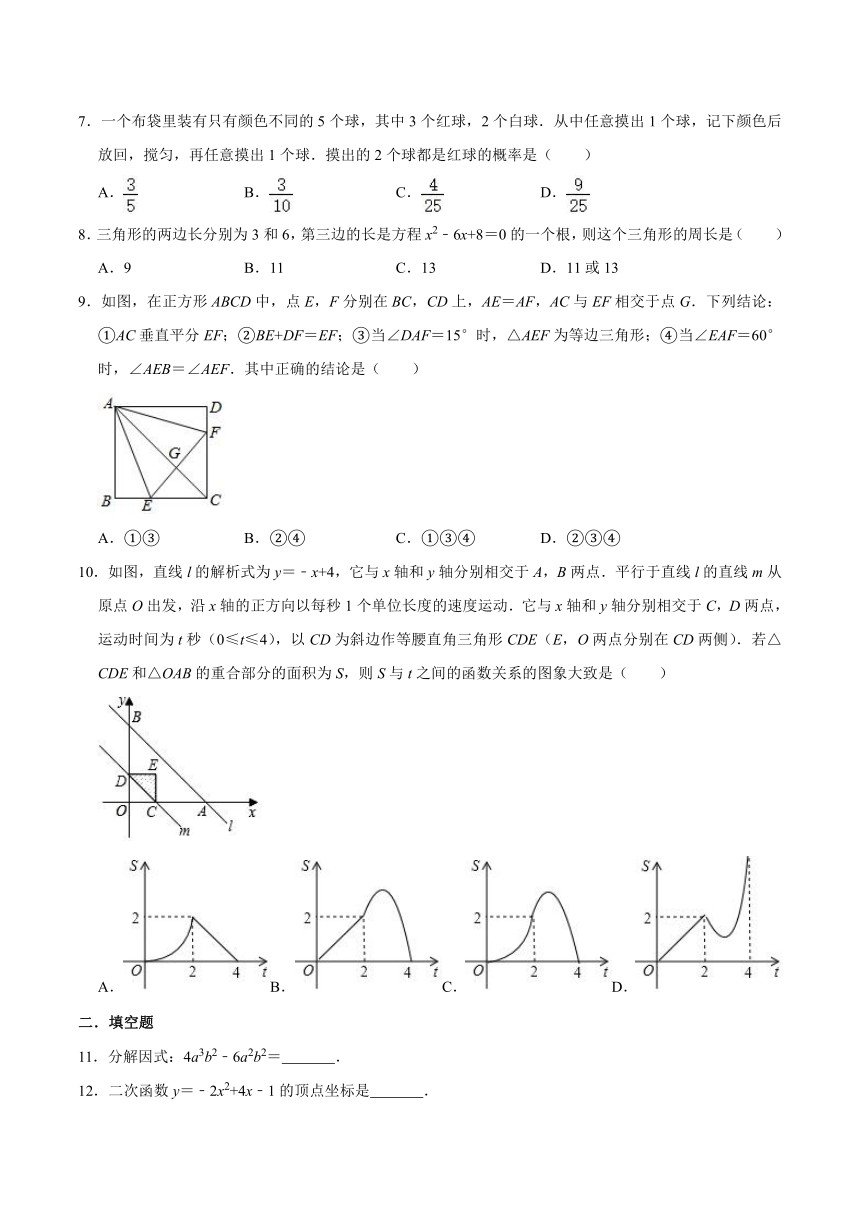
2.如图所示几何体的左视图正确的是( )
A. B. C. D.
3.已知:Rt△ABC中,∠C=90°,cosA=,AB=15,则AC的长是( )
A.3 B.6 C.9 D.12
4.如图,AB是⊙O直径,若∠AOC=140°,则∠D的度数是( )
A.20° B.30° C.40° D.70°
5.如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )
A.2 B.4 C. D.
6.将抛物线y=﹣3x2先向左平移1个单位长度,再向下平移2个单位长度,得到的抛物线的解析式是( )
A.y=﹣3(x﹣1)2﹣2 B.y=﹣3(x﹣1)2+2
C.y=﹣3(x+1)2﹣2 D.y=﹣3(x+1)2+2
7.一个布袋里装有只有颜色不同的5个球,其中3个红球,2个白球.从中任意摸出1个球,记下颜色后放回,搅匀,再任意摸出1个球.摸出的2个球都是红球的概率是( )
A. B. C. D.
8.三角形的两边长分别为3和6,第三边的长是方程x2﹣6x+8=0的一个根,则这个三角形的周长是( )
A.9 B.11 C.13 D.11或13
9.如图,在正方形ABCD中,点E,F分别在BC,CD上,AE=AF,AC与EF相交于点G.下列结论:①AC垂直平分EF;②BE+DF=EF;③当∠DAF=15°时,△AEF为等边三角形;④当∠EAF=60°时,∠AEB=∠AEF.其中正确的结论是( )
A.①③ B.②④ C.①③④ D.②③④
10.如图,直线l的解析式为y=﹣x+4,它与x轴和y轴分别相交于A,B两点.平行于直线l的直线m从原点O出发,沿x轴的正方向以每秒1个单位长度的速度运动.它与x轴和y轴分别相交于C,D两点,运动时间为t秒(0≤t≤4),以CD为斜边作等腰直角三角形CDE(E,O两点分别在CD两侧).若△CDE和△OAB的重合部分的面积为S,则S与t之间的函数关系的图象大致是( )
A.B. C.D.
二.填空题
11.分解因式:4a3b2﹣6a2b2= .
12.二次函数y=﹣2x2+4x﹣1的顶点坐标是 .
13.如图,菱形ABCD的两条对角线AC、BD的长分别为10cm与24cm,点E是AB的中点,则OE= cm.
14.在△ABC中,若,∠A、∠B都是锐角,则∠C= .
15.若关于x的一元二次方程x2﹣2kx+k2﹣k+1=0有两个不相等的实数根,则实数k的取值范围是 .
16.如图,小明为了测量楼房MN的高,在离N点20m的A处放了一个平面镜,小明沿NA方向后退到C点,正好从镜子中看到楼顶M点.若AC=1.6m,小明的眼睛B点离地面的高度BC为1.5m,则楼高MN= m.
17.如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与x轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为,则点P的坐标为 .
18.二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=﹣1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a﹣b+c>2.其中正确的结论的是 .
三.解答题(共11小题)
19.(1)计算:(﹣2017)0+|1﹣|﹣2cos45°+(﹣)﹣2; (2)解不等式组:.
20.如图,等腰△ABC的顶角∠A=36°.请用尺规作图法,在AC上求作一点D,使得△BDC∽△ABC.(保留作图痕迹,不写作法)
21.某学校将周三“阳光体育”项目定为跳绳活动,为此学校准备购置长、短两种跳绳若干.已知长跳绳的单价比短跳绳单价的两倍多4元,且购买2条长跳绳与购买5条短跳绳的费用相同.
(1)两种跳绳的单价各是多少元?
(2)若学校准备用不超过2000元的现金购买200条长、短跳绳,且短跳绳的条数不超过长跳绳的6倍,问学校有几种购买方案可供选择?
22.如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.
23.某校以“我最喜爱的体育项目”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项),根据调查数据绘制了如下不完整的统计表和扇形统计图:
学生选择最喜爱的体育项目统计表
运动项目 频数(人数) 频率
篮球 36 0.30
羽毛球 m 0.25
乒乓球 24 n
跳绳 12 0.10
其它项目 18 0.15
请根据以上图表信息解答下列问题:
(1)统计表中的m= ,n= ;
(2)在扇形统计图中,“篮球”所在扇形的圆心角为 度;
(3)该学校共有2400名学生,据此估计有多少名学生最喜爱乒乓球?
(4)将2名最喜爱篮球的学生和2名最喜爱羽毛球的学生编为一组,从中随机抽取两人,请用列表或画树状图的方法求出所抽取的两人都选择了最喜爱篮球的概率.
24.如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=(m为常数且m≠0)的图象在第二象限交于点C,CD⊥x轴,垂足为D,若OB=2OA=3OD=6.
(1)求一次函数与反比例函数的解析式;
(2)求两个函数图象的另一个交点E的坐标;
(3)请观察图象,直接写出不等式kx+b≤的解集.
25.如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:,AB=8米,AE=10米.(i=1:是指坡面的铅直高度BH与水平宽度AH的比)
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米)
26.如图,在Rt△ABC中,∠ACB=90°,以直角边BC为直径的⊙O交斜边AB于点D.点E为边AC的中点,连接DE并延长交BC的延长线于点F.
(1)求证:直线DE是⊙O的切线;
(2)若∠B=30°,AC=4,求阴影部分的面积.
27.我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[﹣2.5]=﹣3;用<a>表示大于a的最小整数,例如:<2.5>=3,<4>=5,<﹣1.5>=﹣1.解决下列问题:
(1)[﹣4.5]= ,<3.5>= .
(2)若[x]=2,则x的取值范围是 ;若<y>=﹣1,则y的取值范围是 .
(3)已知x,y满足方程组,求x,y的取值范围.
28.如图,抛物线y=﹣x2+bx+c与x轴相交于A,B两点(点A位于点B的左侧),与y轴相交于点C,M是抛物线的顶点,直线x=1是抛物线的对称轴,且点C的坐标为(0,3).
(1)求抛物线的解析式;
(2)已知P为线段MB上一个动点,过点P作PD⊥x轴于点D.若PD=m,△PCD的面积为S.求S与m之间的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,在线段MB上是否存在点P,使△PCD为等腰三角形?如果存在,请写出点P的坐标;如果不存在,请说明理由.
参考答案与试题解析
一.选择题
1.【解答】解:∵反比例函数的图象经过(﹣1,3),∴k=﹣1×3=﹣3,
∴反比例函数解析式为y=﹣.
当x=﹣3时,y=﹣=1,
∴反比例函数y=﹣的图象经过点(﹣3,1),反比例函数y=﹣的图象不经过点(﹣3,﹣1);
当x=﹣时,y=﹣=9,∴反比例函数y=﹣的图象不经过点(﹣,3);
当x=时,y=﹣=﹣9,∴反比例函数y=﹣的图象不经过点(,3).故选:A.
2.【解答】解:从几何体的左面看所得到的图形是:故选:A.
3.【解答】解:在Rt△ABC中,∠C=90°,∵cosA=,∴AC=AB?cosA=15×=9.故选:C.
4.【解答】:∵∠AOC=140°,∴∠BOC=40°,∵∠BOC与∠BDC都对,∴∠D=∠BOC=20°,
故选:A.
5.【解答】解:∵AB∥CD∥EF,∴=,即=,∴BC=,
∴CE=BE﹣BC=12﹣=.故选:C.
6.【解答】解:将抛物线y=﹣3x2向左平移1个单位所得直线解析式为:y=﹣3(x+1)2;
再向下平移2个单位为:y=﹣3(x+1)2﹣2,即y=﹣3(x+1)2﹣2.故选:C.
7.【解答】解:列表得:
红 红 红 白 白
白 (红,白) (红,白) (红,白) (白,白) (白,白)
白 (红,白) (红,白) (红,白) (白,白) (白,白)
红 (红,红) (红,红) (红,红) (红,白) (红,白)
红 (红,红) (红,红) (红,红) (红,白) (红,白)
红 (红,红) (红,红) (红,红) (红,白) (红,白)
∴一共有25种情况,摸出的2个球都是红球的有9种情况,∴摸出的2个球都是红球的概率是.
故选:D.
8.【解答】解:解方程x2﹣6x+8=0得,x=2或4,
则第三边长为2或4.边长为2,3,6不能构成三角形;而3,4,6能构成三角形,
所以三角形的周长为3+4+6=13,故选:C.
9.【解答】解:∵四边形ABCD是正方形,∴AB=AD=BC=CD,∠B=∠D=90°,∠ACD=∠ACB=45°,
∵AB=AD,AE=AF,∴Rt△ABE≌Rt△ADF(HL),∴BE=DF,∴CE=CF,
又∵∠ACD=∠ACB=45°,∴AC垂直平分EF,故①正确;
∵CE=CF,∠BCD=90°,AC垂直平分EF,∴EG=GF,
当AE平分∠BAC时,BE=EG,即BE+DF=EF,故②错误;
∵Rt△ABE≌Rt△ADF,∴∠DAF=∠BAE=15°,∴∠EAF=60°,
又∵AE=AF,∴△AEF是等边三角形,故③正确;
∵AE=AF,∠EAF=60°,∴△AEF是等边三角形,∴∠AEF=60°,
∵∠BAC=45°,∠CAE=30°,∴∠BAE=15°,∴∠AEB=75°≠∠AEF,故④错误;故选:A.
10.【解答】解:当0<t≤2时,S=t2,当2<t≤4时,S=t2﹣(2t﹣4)2=﹣t2+8t﹣8,
观察图象可知,S与t之间的函数关系的图象大致是C.故选:C.
二.填空题
11.【解答】解:4a3b2﹣6a2b2=2a2b2(2a﹣3).故答案为:2a2b2(2a﹣3).
12.【解答】解:∵y=﹣2x2+4x﹣1=﹣2(x2﹣2x)﹣1=﹣2[(x﹣1)2﹣1]﹣1=﹣2(x﹣1)2+1,
∴二次函数的图象的顶点坐标为(1,1),故答案为(1,1).
13.【解答】解:∵四边形ABCD是菱形,AC=10cm,BD=24cm,
∴OA=OC=AC=5cm,OB=OD=BD=12cm,AC⊥BD,
∴AD===13(cm),
又∵点E是AB中点,∴OE是△DAB的中位线,∴OE=AD=6.5cm.故答案为:6.5.
14.【解答】解:∵,∴sinA=,cosB=,
∴∠A=45°,∠B=30°,
故可得∠C=180°﹣45°﹣30°=105°.
故答案为:105°.
15.【解答】解:∵原方程有两个不相等的实数根,
∴△=b2﹣4ac=(2k)2﹣4(k2﹣k+1)=4k﹣4>0,解得k>1;故答案为:k>1.
16.【解答】解:∵BC⊥CA,MN⊥AN,∴∠C=∠N=90°,
∵∠BAC=∠MAN,∴△BCA∽△MNA.∴,即,∴MN=(m),
答:楼房MN的高度为m,故答案为:.
17.【解答】解:过点P作PD⊥x轴于点D,连接OP,
∵A(6,0),PD⊥OA,∴OD=OA=3,
在Rt△OPD中,∵OP=,OD=3,∴PD===2,∴P(3,2).
故答案为:(3,2).
18.【解答】解:∵抛物线开口向下,∴a<0,∵抛物线的对称轴为直线x=﹣=﹣1,∴b=2a<0,
∵抛物线与y轴的交点在x轴上方,∴c>0,∴abc>0,所以①正确;
∵抛物线与x轴有2个交点,∴△=b2﹣4ac>0,所以②正确;∵b=2a,∴2a﹣b=0,所以③错误;
∵抛物线开口向下,x=﹣1是对称轴,所以x=﹣1对应的y值是最大值,∴a﹣b+c>2,所以④正确.
故答案是:①②④.
三.解答题(共11小题)
19.【解答】解:(1)原式=1+﹣1﹣2×+9=1+﹣1﹣+9=9;
(2)解不等式x﹣3(x﹣2)≥4,得:x≤1,解不等式>x﹣1,得:x>﹣4,
则不等式组的解集为﹣4<x≤1
20.【解答】解:如图,线段BD即为所求.
21.【解答】解:(1)设长跳绳的单价是x元,短跳绳的单价为y元.
由题意得:,解得:.答:长跳绳单价是20元,短跳绳的单价是8元.
(2)设学校购买a条长跳绳,则购买(200﹣a)条短跳绳,
由题意得:,解得:.
∵a为正整数,∴a的整数值为29,30,31,32,33.答:学校共有5种购买方案可供选择.
22.【解答】证明:(1)∵四边形ABCD是平行四边形,∴AB∥DC,AB=DC,∴∠ABF=∠ECF,
∵EC=DC,∴AB=EC,
在△ABF和△ECF中,∵∠ABF=∠ECF,∠AFB=∠EFC,AB=EC,∴△ABF≌△ECF(AAS).
(2)∵AB=EC,AB∥EC,∴四边形ABEC是平行四边形,∴FA=FE,FB=FC,
∵四边形ABCD是平行四边形,∴∠ABC=∠D,
又∵∠AFC=2∠D,∴∠AFC=2∠ABC,∵∠AFC=∠ABC+∠BAF,∴∠ABC=∠BAF,∴FA=FB,
∴FA=FE=FB=FC,∴AE=BC,∴平行四边形ABEC是矩形.
23.【解答】解:(1)∵36÷0.3=120(人),∴m=120×0.25=30(人),n=24÷120=0.20,
故答案为:30,0.20;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为:360°×0.3=108°;故答案为:108;
(3)根据题意得:2400×0.2=480(人),答:估计有480名学生最喜爱乒乓球;
(4)根据题意画树状图如下:
由图可知总共有12种结果,每种结果出现的可能性相同,其中两人都选择篮球的结果有2种,所以抽取的两人都选择了最喜爱篮球的概率是=.
24.【解答】解:(1)∵OB=2OA=3OD=6,∴OB=6,OA=3,OD=2,∵CD⊥OA,∴DC∥OB,
∴=,∴=,∴CD=10,∴点C坐标是(﹣2,10),
∵B(0,6),A(3,0),∴,解得,
∴一次函数为y=﹣2x+6.
∵反比例函数y=经过点C(﹣2,10),∴m=﹣20,∴反比例函数解析式为y=﹣.
(2)由解得或,∴E的坐标为(5,﹣4).
(3)由图象可知kx+b≤的解集是:﹣2≤x<0或x≥5.
25.【解答】解:(1)在Rt△ABH中,tan∠BAH==,∴∠BAH=30°,∴BH=AB=4米;
(2)过B作BG⊥DE于G,如图所示:
由(1)得:BH=4米,AH=4米,∴BG=AH+AE=4+10(米),
Rt△BGC中,∠CBG=45°,∴CG=BG=4+10(米).
Rt△ADE中,∠DAE=60°,AE=10米,∴DE=AE=10米.
∴CD=CG+GE﹣DE=4+10+4﹣10=14﹣6≈3.6(米).
答:广告牌CD的高度约为3.6米.
26.【解答】(1)证明:连接OD、CD,
∵OC=OD,∴∠OCD=∠ODC,又∵BC是⊙O的直径,∴∠BDC=90°,
∴△ACD是直角三角形,
又∵点E是斜边AC的中点,∴EC=ED,∴∠ECD=∠EDC
又∵∠ECD+∠OCD=∠ACB=90度,∴∠EDC+∠ODC=∠ODE=90°,
∴直线DE是⊙O的切线;
(2)解:由(1)已证:∠ODF=90°,
∴∠B=30°,
∴∠DOF=60°,
∴∠F=30°,
在Rt△ABC中,AC=4,
∴BC===4,
∴,
在Rt△ODF中,,
∴阴影部分的面积为:=.
27.【解答】解:(1)由题意得,[﹣4.5]=﹣5,<3.5>=4;
(2)∵[x]=2,∴x的取值范围是2≤x<3;∵<y>=﹣1,∴y的取值范围是﹣2≤y<﹣1;
(3)解方程组得:,∴x,y的取值范围分别为﹣1≤x<0,2≤y<3.
故答案为:﹣5,4;2≤x<3,﹣2≤y<﹣1.
28.【解答】解:(1)∵直线x=1是抛物线的对称轴,且点C的坐标为(0,3),
∴c=3,﹣=1,∴b=2,∴抛物线的解析式为:y=﹣x2+2x+3.
(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴点M(1,4),
∵抛物线的解析式为:y=﹣x2+2x+3与x轴相交于A,B两点(点A位于点B的左侧),
∴0=﹣x2+2x+3,∴x1=3,x2=﹣1,∴点A(﹣1,0),点B(3,0),
∵点M(1,4),点B(3,0),∴直线BM解析式为y=﹣2x+6,
∵点P在直线BM上,且PD⊥x轴于点D,PD=m,∴点P(3﹣,m),
∴S△PCD=×PD×OD=m×(3﹣m)=﹣m2+m,
∵点P在线段BM上,且点M(1,4),点B(3,0),
∴0<m≤4,∴S与m之间的函数关系式为S=﹣m2+m(0<m≤4).
(3)存在,
若PC=PD=m时,
∵PD=m,点P(3﹣,m),点C(0,3),∴(3﹣﹣0)2+(m﹣3)2=m2,
∴m1=18+6(舍去),m2=18﹣6,∴点P(﹣6+3,18﹣6).
若DC=PD=m时,∴(3﹣﹣0)2+(﹣3)2=m2,
∴m3=﹣2﹣2(舍去),m4=﹣2+2,
∴点P(4﹣,﹣2+2).
若DC=PC时,
∴(3﹣﹣0)2+(m﹣3)2=(3﹣﹣0)2+(﹣3)2,
∴m5=0(舍去),m6=6(舍去),
综上所述:当点P的坐标为:(﹣6+3,18﹣6)或(4﹣,﹣2+2)时,使△PCD为等腰三角形.
一.选择题
1.若反比例函数的图象经过(﹣1,3),则这个函数的图象一定过( )
A.(﹣3,1) B.(﹣,3) C.(﹣3,﹣1) D.(,3)
2.如图所示几何体的左视图正确的是( )
A. B. C. D.
3.已知:Rt△ABC中,∠C=90°,cosA=,AB=15,则AC的长是( )
A.3 B.6 C.9 D.12
4.如图,AB是⊙O直径,若∠AOC=140°,则∠D的度数是( )
A.20° B.30° C.40° D.70°
5.如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )
A.2 B.4 C. D.
6.将抛物线y=﹣3x2先向左平移1个单位长度,再向下平移2个单位长度,得到的抛物线的解析式是( )
A.y=﹣3(x﹣1)2﹣2 B.y=﹣3(x﹣1)2+2
C.y=﹣3(x+1)2﹣2 D.y=﹣3(x+1)2+2
7.一个布袋里装有只有颜色不同的5个球,其中3个红球,2个白球.从中任意摸出1个球,记下颜色后放回,搅匀,再任意摸出1个球.摸出的2个球都是红球的概率是( )
A. B. C. D.
8.三角形的两边长分别为3和6,第三边的长是方程x2﹣6x+8=0的一个根,则这个三角形的周长是( )
A.9 B.11 C.13 D.11或13
9.如图,在正方形ABCD中,点E,F分别在BC,CD上,AE=AF,AC与EF相交于点G.下列结论:①AC垂直平分EF;②BE+DF=EF;③当∠DAF=15°时,△AEF为等边三角形;④当∠EAF=60°时,∠AEB=∠AEF.其中正确的结论是( )
A.①③ B.②④ C.①③④ D.②③④
10.如图,直线l的解析式为y=﹣x+4,它与x轴和y轴分别相交于A,B两点.平行于直线l的直线m从原点O出发,沿x轴的正方向以每秒1个单位长度的速度运动.它与x轴和y轴分别相交于C,D两点,运动时间为t秒(0≤t≤4),以CD为斜边作等腰直角三角形CDE(E,O两点分别在CD两侧).若△CDE和△OAB的重合部分的面积为S,则S与t之间的函数关系的图象大致是( )
A.B. C.D.
二.填空题
11.分解因式:4a3b2﹣6a2b2= .
12.二次函数y=﹣2x2+4x﹣1的顶点坐标是 .
13.如图,菱形ABCD的两条对角线AC、BD的长分别为10cm与24cm,点E是AB的中点,则OE= cm.
14.在△ABC中,若,∠A、∠B都是锐角,则∠C= .
15.若关于x的一元二次方程x2﹣2kx+k2﹣k+1=0有两个不相等的实数根,则实数k的取值范围是 .
16.如图,小明为了测量楼房MN的高,在离N点20m的A处放了一个平面镜,小明沿NA方向后退到C点,正好从镜子中看到楼顶M点.若AC=1.6m,小明的眼睛B点离地面的高度BC为1.5m,则楼高MN= m.
17.如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与x轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为,则点P的坐标为 .
18.二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=﹣1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a﹣b+c>2.其中正确的结论的是 .
三.解答题(共11小题)
19.(1)计算:(﹣2017)0+|1﹣|﹣2cos45°+(﹣)﹣2; (2)解不等式组:.
20.如图,等腰△ABC的顶角∠A=36°.请用尺规作图法,在AC上求作一点D,使得△BDC∽△ABC.(保留作图痕迹,不写作法)
21.某学校将周三“阳光体育”项目定为跳绳活动,为此学校准备购置长、短两种跳绳若干.已知长跳绳的单价比短跳绳单价的两倍多4元,且购买2条长跳绳与购买5条短跳绳的费用相同.
(1)两种跳绳的单价各是多少元?
(2)若学校准备用不超过2000元的现金购买200条长、短跳绳,且短跳绳的条数不超过长跳绳的6倍,问学校有几种购买方案可供选择?
22.如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.
23.某校以“我最喜爱的体育项目”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项),根据调查数据绘制了如下不完整的统计表和扇形统计图:
学生选择最喜爱的体育项目统计表
运动项目 频数(人数) 频率
篮球 36 0.30
羽毛球 m 0.25
乒乓球 24 n
跳绳 12 0.10
其它项目 18 0.15
请根据以上图表信息解答下列问题:
(1)统计表中的m= ,n= ;
(2)在扇形统计图中,“篮球”所在扇形的圆心角为 度;
(3)该学校共有2400名学生,据此估计有多少名学生最喜爱乒乓球?
(4)将2名最喜爱篮球的学生和2名最喜爱羽毛球的学生编为一组,从中随机抽取两人,请用列表或画树状图的方法求出所抽取的两人都选择了最喜爱篮球的概率.
24.如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=(m为常数且m≠0)的图象在第二象限交于点C,CD⊥x轴,垂足为D,若OB=2OA=3OD=6.
(1)求一次函数与反比例函数的解析式;
(2)求两个函数图象的另一个交点E的坐标;
(3)请观察图象,直接写出不等式kx+b≤的解集.
25.如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:,AB=8米,AE=10米.(i=1:是指坡面的铅直高度BH与水平宽度AH的比)
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米)
26.如图,在Rt△ABC中,∠ACB=90°,以直角边BC为直径的⊙O交斜边AB于点D.点E为边AC的中点,连接DE并延长交BC的延长线于点F.
(1)求证:直线DE是⊙O的切线;
(2)若∠B=30°,AC=4,求阴影部分的面积.
27.我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[﹣2.5]=﹣3;用<a>表示大于a的最小整数,例如:<2.5>=3,<4>=5,<﹣1.5>=﹣1.解决下列问题:
(1)[﹣4.5]= ,<3.5>= .
(2)若[x]=2,则x的取值范围是 ;若<y>=﹣1,则y的取值范围是 .
(3)已知x,y满足方程组,求x,y的取值范围.
28.如图,抛物线y=﹣x2+bx+c与x轴相交于A,B两点(点A位于点B的左侧),与y轴相交于点C,M是抛物线的顶点,直线x=1是抛物线的对称轴,且点C的坐标为(0,3).
(1)求抛物线的解析式;
(2)已知P为线段MB上一个动点,过点P作PD⊥x轴于点D.若PD=m,△PCD的面积为S.求S与m之间的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,在线段MB上是否存在点P,使△PCD为等腰三角形?如果存在,请写出点P的坐标;如果不存在,请说明理由.
参考答案与试题解析
一.选择题
1.【解答】解:∵反比例函数的图象经过(﹣1,3),∴k=﹣1×3=﹣3,
∴反比例函数解析式为y=﹣.
当x=﹣3时,y=﹣=1,
∴反比例函数y=﹣的图象经过点(﹣3,1),反比例函数y=﹣的图象不经过点(﹣3,﹣1);
当x=﹣时,y=﹣=9,∴反比例函数y=﹣的图象不经过点(﹣,3);
当x=时,y=﹣=﹣9,∴反比例函数y=﹣的图象不经过点(,3).故选:A.
2.【解答】解:从几何体的左面看所得到的图形是:故选:A.
3.【解答】解:在Rt△ABC中,∠C=90°,∵cosA=,∴AC=AB?cosA=15×=9.故选:C.
4.【解答】:∵∠AOC=140°,∴∠BOC=40°,∵∠BOC与∠BDC都对,∴∠D=∠BOC=20°,
故选:A.
5.【解答】解:∵AB∥CD∥EF,∴=,即=,∴BC=,
∴CE=BE﹣BC=12﹣=.故选:C.
6.【解答】解:将抛物线y=﹣3x2向左平移1个单位所得直线解析式为:y=﹣3(x+1)2;
再向下平移2个单位为:y=﹣3(x+1)2﹣2,即y=﹣3(x+1)2﹣2.故选:C.
7.【解答】解:列表得:
红 红 红 白 白
白 (红,白) (红,白) (红,白) (白,白) (白,白)
白 (红,白) (红,白) (红,白) (白,白) (白,白)
红 (红,红) (红,红) (红,红) (红,白) (红,白)
红 (红,红) (红,红) (红,红) (红,白) (红,白)
红 (红,红) (红,红) (红,红) (红,白) (红,白)
∴一共有25种情况,摸出的2个球都是红球的有9种情况,∴摸出的2个球都是红球的概率是.
故选:D.
8.【解答】解:解方程x2﹣6x+8=0得,x=2或4,
则第三边长为2或4.边长为2,3,6不能构成三角形;而3,4,6能构成三角形,
所以三角形的周长为3+4+6=13,故选:C.
9.【解答】解:∵四边形ABCD是正方形,∴AB=AD=BC=CD,∠B=∠D=90°,∠ACD=∠ACB=45°,
∵AB=AD,AE=AF,∴Rt△ABE≌Rt△ADF(HL),∴BE=DF,∴CE=CF,
又∵∠ACD=∠ACB=45°,∴AC垂直平分EF,故①正确;
∵CE=CF,∠BCD=90°,AC垂直平分EF,∴EG=GF,
当AE平分∠BAC时,BE=EG,即BE+DF=EF,故②错误;
∵Rt△ABE≌Rt△ADF,∴∠DAF=∠BAE=15°,∴∠EAF=60°,
又∵AE=AF,∴△AEF是等边三角形,故③正确;
∵AE=AF,∠EAF=60°,∴△AEF是等边三角形,∴∠AEF=60°,
∵∠BAC=45°,∠CAE=30°,∴∠BAE=15°,∴∠AEB=75°≠∠AEF,故④错误;故选:A.
10.【解答】解:当0<t≤2时,S=t2,当2<t≤4时,S=t2﹣(2t﹣4)2=﹣t2+8t﹣8,
观察图象可知,S与t之间的函数关系的图象大致是C.故选:C.
二.填空题
11.【解答】解:4a3b2﹣6a2b2=2a2b2(2a﹣3).故答案为:2a2b2(2a﹣3).
12.【解答】解:∵y=﹣2x2+4x﹣1=﹣2(x2﹣2x)﹣1=﹣2[(x﹣1)2﹣1]﹣1=﹣2(x﹣1)2+1,
∴二次函数的图象的顶点坐标为(1,1),故答案为(1,1).
13.【解答】解:∵四边形ABCD是菱形,AC=10cm,BD=24cm,
∴OA=OC=AC=5cm,OB=OD=BD=12cm,AC⊥BD,
∴AD===13(cm),
又∵点E是AB中点,∴OE是△DAB的中位线,∴OE=AD=6.5cm.故答案为:6.5.
14.【解答】解:∵,∴sinA=,cosB=,
∴∠A=45°,∠B=30°,
故可得∠C=180°﹣45°﹣30°=105°.
故答案为:105°.
15.【解答】解:∵原方程有两个不相等的实数根,
∴△=b2﹣4ac=(2k)2﹣4(k2﹣k+1)=4k﹣4>0,解得k>1;故答案为:k>1.
16.【解答】解:∵BC⊥CA,MN⊥AN,∴∠C=∠N=90°,
∵∠BAC=∠MAN,∴△BCA∽△MNA.∴,即,∴MN=(m),
答:楼房MN的高度为m,故答案为:.
17.【解答】解:过点P作PD⊥x轴于点D,连接OP,
∵A(6,0),PD⊥OA,∴OD=OA=3,
在Rt△OPD中,∵OP=,OD=3,∴PD===2,∴P(3,2).
故答案为:(3,2).
18.【解答】解:∵抛物线开口向下,∴a<0,∵抛物线的对称轴为直线x=﹣=﹣1,∴b=2a<0,
∵抛物线与y轴的交点在x轴上方,∴c>0,∴abc>0,所以①正确;
∵抛物线与x轴有2个交点,∴△=b2﹣4ac>0,所以②正确;∵b=2a,∴2a﹣b=0,所以③错误;
∵抛物线开口向下,x=﹣1是对称轴,所以x=﹣1对应的y值是最大值,∴a﹣b+c>2,所以④正确.
故答案是:①②④.
三.解答题(共11小题)
19.【解答】解:(1)原式=1+﹣1﹣2×+9=1+﹣1﹣+9=9;
(2)解不等式x﹣3(x﹣2)≥4,得:x≤1,解不等式>x﹣1,得:x>﹣4,
则不等式组的解集为﹣4<x≤1
20.【解答】解:如图,线段BD即为所求.
21.【解答】解:(1)设长跳绳的单价是x元,短跳绳的单价为y元.
由题意得:,解得:.答:长跳绳单价是20元,短跳绳的单价是8元.
(2)设学校购买a条长跳绳,则购买(200﹣a)条短跳绳,
由题意得:,解得:.
∵a为正整数,∴a的整数值为29,30,31,32,33.答:学校共有5种购买方案可供选择.
22.【解答】证明:(1)∵四边形ABCD是平行四边形,∴AB∥DC,AB=DC,∴∠ABF=∠ECF,
∵EC=DC,∴AB=EC,
在△ABF和△ECF中,∵∠ABF=∠ECF,∠AFB=∠EFC,AB=EC,∴△ABF≌△ECF(AAS).
(2)∵AB=EC,AB∥EC,∴四边形ABEC是平行四边形,∴FA=FE,FB=FC,
∵四边形ABCD是平行四边形,∴∠ABC=∠D,
又∵∠AFC=2∠D,∴∠AFC=2∠ABC,∵∠AFC=∠ABC+∠BAF,∴∠ABC=∠BAF,∴FA=FB,
∴FA=FE=FB=FC,∴AE=BC,∴平行四边形ABEC是矩形.
23.【解答】解:(1)∵36÷0.3=120(人),∴m=120×0.25=30(人),n=24÷120=0.20,
故答案为:30,0.20;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为:360°×0.3=108°;故答案为:108;
(3)根据题意得:2400×0.2=480(人),答:估计有480名学生最喜爱乒乓球;
(4)根据题意画树状图如下:
由图可知总共有12种结果,每种结果出现的可能性相同,其中两人都选择篮球的结果有2种,所以抽取的两人都选择了最喜爱篮球的概率是=.
24.【解答】解:(1)∵OB=2OA=3OD=6,∴OB=6,OA=3,OD=2,∵CD⊥OA,∴DC∥OB,
∴=,∴=,∴CD=10,∴点C坐标是(﹣2,10),
∵B(0,6),A(3,0),∴,解得,
∴一次函数为y=﹣2x+6.
∵反比例函数y=经过点C(﹣2,10),∴m=﹣20,∴反比例函数解析式为y=﹣.
(2)由解得或,∴E的坐标为(5,﹣4).
(3)由图象可知kx+b≤的解集是:﹣2≤x<0或x≥5.
25.【解答】解:(1)在Rt△ABH中,tan∠BAH==,∴∠BAH=30°,∴BH=AB=4米;
(2)过B作BG⊥DE于G,如图所示:
由(1)得:BH=4米,AH=4米,∴BG=AH+AE=4+10(米),
Rt△BGC中,∠CBG=45°,∴CG=BG=4+10(米).
Rt△ADE中,∠DAE=60°,AE=10米,∴DE=AE=10米.
∴CD=CG+GE﹣DE=4+10+4﹣10=14﹣6≈3.6(米).
答:广告牌CD的高度约为3.6米.
26.【解答】(1)证明:连接OD、CD,
∵OC=OD,∴∠OCD=∠ODC,又∵BC是⊙O的直径,∴∠BDC=90°,
∴△ACD是直角三角形,
又∵点E是斜边AC的中点,∴EC=ED,∴∠ECD=∠EDC
又∵∠ECD+∠OCD=∠ACB=90度,∴∠EDC+∠ODC=∠ODE=90°,
∴直线DE是⊙O的切线;
(2)解:由(1)已证:∠ODF=90°,
∴∠B=30°,
∴∠DOF=60°,
∴∠F=30°,
在Rt△ABC中,AC=4,
∴BC===4,
∴,
在Rt△ODF中,,
∴阴影部分的面积为:=.
27.【解答】解:(1)由题意得,[﹣4.5]=﹣5,<3.5>=4;
(2)∵[x]=2,∴x的取值范围是2≤x<3;∵<y>=﹣1,∴y的取值范围是﹣2≤y<﹣1;
(3)解方程组得:,∴x,y的取值范围分别为﹣1≤x<0,2≤y<3.
故答案为:﹣5,4;2≤x<3,﹣2≤y<﹣1.
28.【解答】解:(1)∵直线x=1是抛物线的对称轴,且点C的坐标为(0,3),
∴c=3,﹣=1,∴b=2,∴抛物线的解析式为:y=﹣x2+2x+3.
(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴点M(1,4),
∵抛物线的解析式为:y=﹣x2+2x+3与x轴相交于A,B两点(点A位于点B的左侧),
∴0=﹣x2+2x+3,∴x1=3,x2=﹣1,∴点A(﹣1,0),点B(3,0),
∵点M(1,4),点B(3,0),∴直线BM解析式为y=﹣2x+6,
∵点P在直线BM上,且PD⊥x轴于点D,PD=m,∴点P(3﹣,m),
∴S△PCD=×PD×OD=m×(3﹣m)=﹣m2+m,
∵点P在线段BM上,且点M(1,4),点B(3,0),
∴0<m≤4,∴S与m之间的函数关系式为S=﹣m2+m(0<m≤4).
(3)存在,
若PC=PD=m时,
∵PD=m,点P(3﹣,m),点C(0,3),∴(3﹣﹣0)2+(m﹣3)2=m2,
∴m1=18+6(舍去),m2=18﹣6,∴点P(﹣6+3,18﹣6).
若DC=PD=m时,∴(3﹣﹣0)2+(﹣3)2=m2,
∴m3=﹣2﹣2(舍去),m4=﹣2+2,
∴点P(4﹣,﹣2+2).
若DC=PC时,
∴(3﹣﹣0)2+(m﹣3)2=(3﹣﹣0)2+(﹣3)2,
∴m5=0(舍去),m6=6(舍去),
综上所述:当点P的坐标为:(﹣6+3,18﹣6)或(4﹣,﹣2+2)时,使△PCD为等腰三角形.
同课章节目录
