人教版数学五年级下册 第七单元 整理与复习 课件(28张ppt)
文档属性
| 名称 | 人教版数学五年级下册 第七单元 整理与复习 课件(28张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 00:00:00 | ||
图片预览



文档简介
五年级下册 数学 第七单元
折线统计图整理与复习
学习目标
1.认识单式折线统计图和复式折线统计图及其特征,能根据需要选择折线统计图直观、有效地表示数据,并能对数据进行简单的分析和预测。
2.经历根据折线统计图解决简单实际问题的过程,掌握对简单数据进行分析的方法。
3.通过对数据的分析,体会统计在生活中的作用和意义,提高数学学习兴趣。
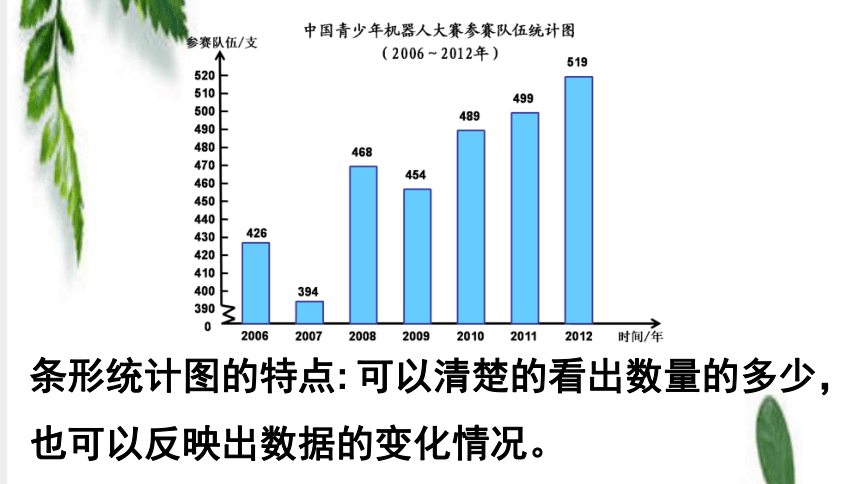
条形统计图的特点:
可以清楚的看出数量的多少,
也可以反映出数据的变化情况。
390
0
400
410
420
430
440
450
460
470
480
490
500
510
520
2006
2007
2008
2009
2010
2011
2012
年份
参赛队伍/支
426
394
468
454
489
499
519
中国青少年机器人大赛参赛队伍统计图
(2006—2012年)
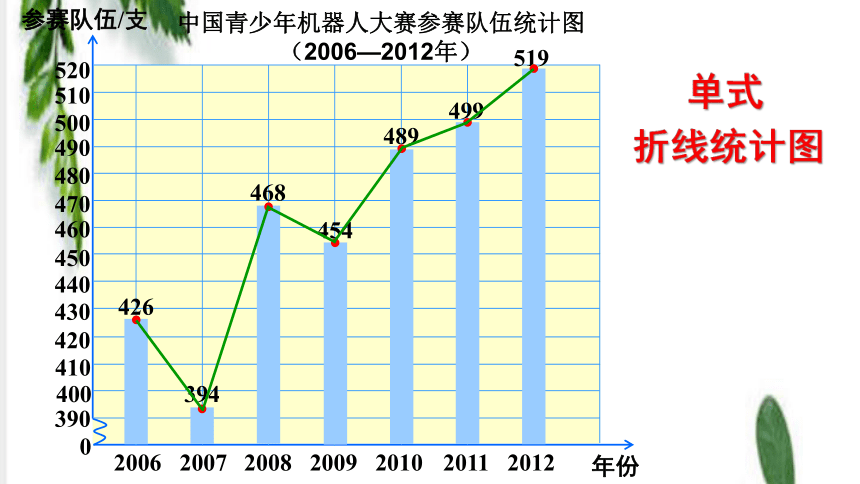
折线统计图
单式
折线统计图不仅能够通过点的高低反映数据的多少,还能通过线的起伏反映数据的增减变化,能从中发现数量的变化趋势,并能对将来的发展趋势进行预测。
折线统计图的特点:
中国青少年机器人大赛参赛队伍统计图
(2006—2012年)
390
0
400
410
420
430
440
450
460
470
480
490
500
510
520
2006
2007
2008
2009
2010
2011
2012
年份
参赛队伍/支
426
394
468
454
489
499
519
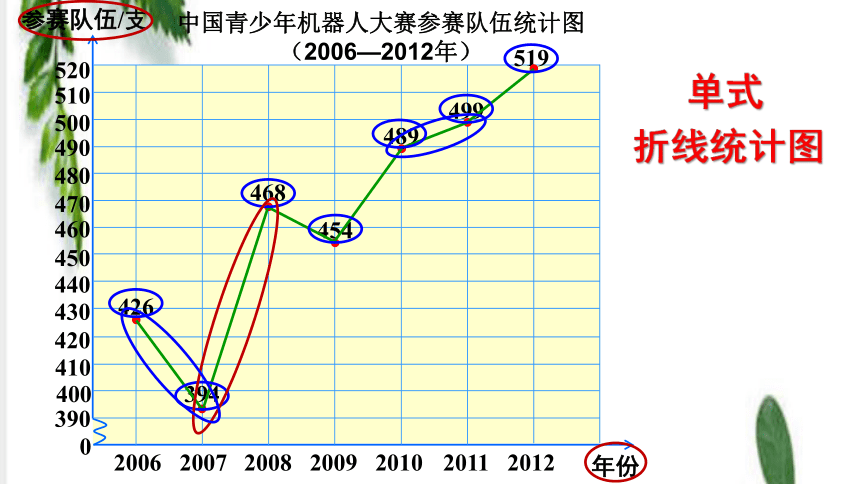
折线统计图
单式
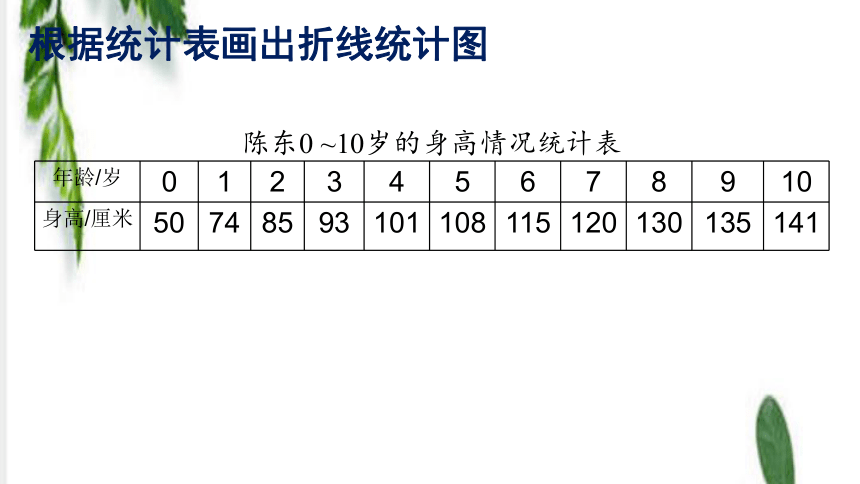
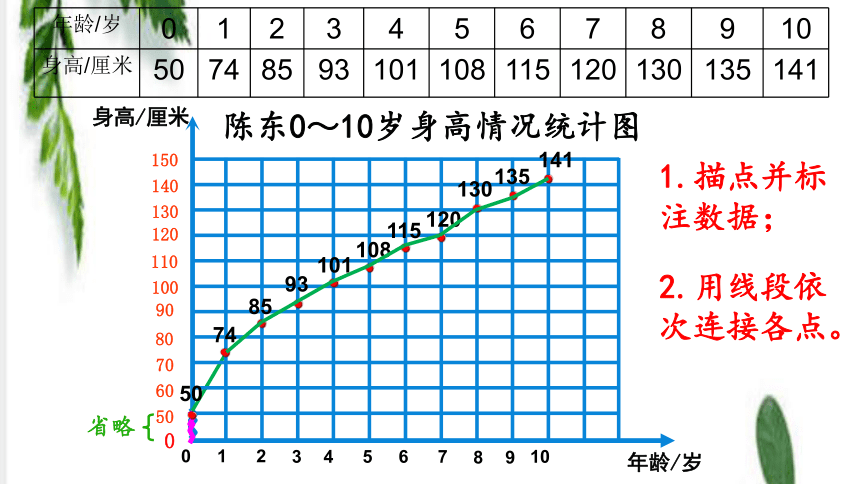
根据统计表画出折线统计图
年龄/岁
0
1
2
3
4
5
6
7
8
9
10
身高/厘米
50
74
85
93
101
108
115
120
130
135
141
陈东0 ~10岁的身高情况统计表
0
陈东0~10岁身高情况统计图
身高/厘米
50
60
70
80
90
100
110
120
130
140
150
0
1
2
3
4
年龄/岁
5
6
7
8
9
10
50
74
85
93
101
108
115
120
130
135
141
省略
1.描点并标注数据;
2.用线段依次连接各点。
年龄/岁
0
1
2
3
4
5
6
7
8
9
10
身高/厘米
50
74
85
93
101
108
115
120
130
135
141
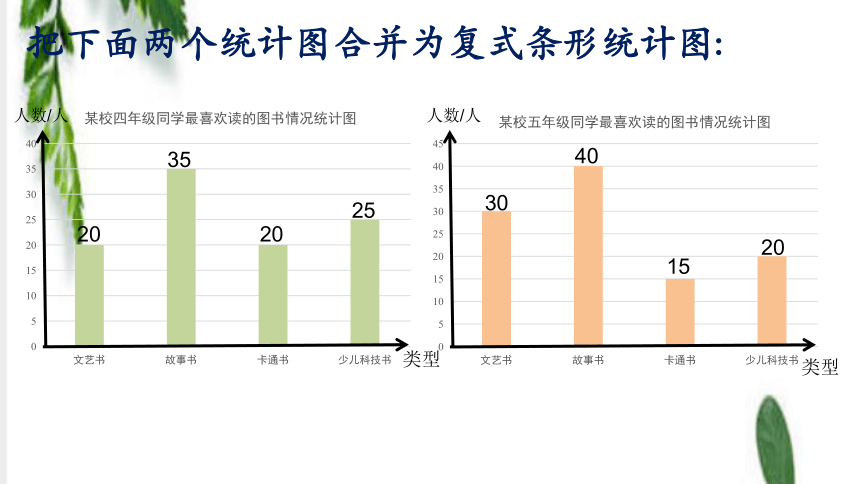
人数/人
类型
类型
人数/人
20
20
35
25
20
15
40
30
把下面两个统计图合并为复式条形统计图:
人数/人
类型
20
20
35
25
20
15
40
30
复式条形统计图不仅能看出数量的多少,还便于比较两组数据的多少。
5.5
0
6.0
6.5
7.0
7.5
8.0
8.5
9.0
9.5
10.0
10.5
2001
2002
2003
2004
2005
2006
2007
年份
人口数/万人
2008
2009
2010
11.0
6.20
5.73
8.09
8.25
8.12
10.08
9.67
9.23
5.76
10.02
2001-2010年上海出生人口数统计图
5.5
0
6.0
6.5
7.0
7.5
8.0
8.5
9.0
9.5
10.0
10.5
2001
2002
2003
2004
2005
2006
2007
年份
2008
2009
2010
11.0
人口数/万人
2001-2010年上海死亡人口数统计图
9.67
10.07
9.65
10.23
9.80
10.22
10.70
10.67
9.34
10.87
5.5
0
6.0
6.5
7.0
7.5
8.0
8.5
9.0
9.5
10.0
10.5
2001
2002
2003
2004
2005
2006
2007
年份
人口数/万人
2008
2009
2010
11.0
6.20
5.73
8.09
8.25
8.12
10.08
9.67
9.23
5.76
10.02
2001-2010年上海出生人口和死亡人口数统计图
9.67
10.07
9.65
10.23
9.80
10.22
10.70
10.67
9.34
10.87
出生人口
死亡人口
5.5
0
6.0
6.5
7.0
7.5
8.0
8.5
9.0
9.5
10.0
10.5
2001
2002
2003
2004
2005
2006
2007
年份
人口数/万人
2008
2009
2010
11.0
6.20
5.73
8.09
8.25
8.12
10.08
9.67
9.23
5.76
10.02
9.67
10.07
9.65
10.23
9.80
10.22
10.70
10.67
9.34
10.87
2001-2010年上海出生人口和死亡人口数统计图
出生人口
死亡人口
绘制复式折线统计图与单式折线统计图的步骤相同,按数据描出各点并标明数据,用线段依次连接各点,
在一个统计图里,用两条或两条以上折线分别表示两条不同的数据,这样的折线统计图叫做复式折线统计图。
用图例标明两条折线的含义。
复式折线统计图不仅能看出数量增减变化的情况,而且便于比较出两组数据的差异和变化趋势。
①描点 ②标数 ③连线 ④标图例
5.5
0
6.0
6.5
7.0
7.5
8.0
8.5
9.0
9.5
10.0
10.5
2001
2002
2003
2004
2005
2006
2007
年份
人口数/万人
2008
2009
2010
11.0
6.20
5.73
8.09
8.25
8.12
10.08
9.67
9.23
5.76
10.02
9.67
10.07
9.65
10.23
9.80
10.22
10.70
10.67
9.34
10.87
2001-2010年上海出生人口和死亡人口数统计图
出生人口
死亡人口
39
38
37
36
0
6
时间/时
体温/℃
12
18
0
6
12
18
0
6
39.5
37.1
38
39.2
38
37
36.8
37.2
一个病人住院期间体温变化情况统计图
18
12
5月23日
5月24日
5月25日
1.根据统计图回答问题。
(5)从体温上看,这位病人的病情是在恶化还是在好转?
为什么?
(1)护士每 小时给病人测一次体温。
(2)这位病人体温最高是 ℃,最低是 ℃。
(3)病人在5月24日12时
的体温是 。
(4)图中虚线表示 。
6
39.5
36.8
37.5℃
人的正常体温
好转
因为体温趋于正常
2.
2000年最多,
2010年最少。
2002年最多,
2010年最少。
从整体上看,学龄儿童人数和入学人数都在逐年减少,并且越来越接近,说明学龄儿童入学率在稳步提高。
11310.4-11150.0=160.4(万人)
9501.5-9473.3=28.2(万人)
没上学人数=学龄儿童人数-入学人数
销售量/台
0
30
35
40
45
50
55
60
65
70
80
85
1
2
3
4
时间/月
5
6
7
8
9
10
11
12
75
70
80
40
甲、乙两种品牌空调2019年销售情况统计图
61
54
41
38
42
46
35
46
60
75
39
38
41
50
46
50
84
39
42
52
55
甲品牌
乙品牌
3.
14
25
(40+39+38+41+50+46+39+42+50+52+55+84)÷12=48(台)
(1)乙品牌空调从( )
月到( )月的销售量
上升最快。
(2)从2月到6月,( )
品牌空调的销售量呈下
降趋势。
(3)乙品牌空调平均每
月销售( )台。
(4)甲品牌空调7月份销售量是12月份的(——),
乙品牌空调1月份的销售量是5月份的(——)。
11
12
甲
48
42
75
40
50
4
5
4.李明和丁阳参加学校运动会一分钟跳绳比赛,提前十天进行训练,每天测试成绩如下表。(单位:次)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
1
2
3
4
5
6
7
8
9
10
李明
152
155
158
160
157
159
162
165
165
167
丁阳
153
154
159
155
160
164
158
162
160
165
第几
天
成
绩
(次
/分)
姓名
(1)根据表中数据完成统计图。
150
0
152
154
156
158
160
162
164
166
168
170
1
2
3
4
5
6
7
时间/天
8
9
10
172
成绩 /(次/分)
李明、丁阳一分钟跳绳情况统计图
152
155
158
160
157
159
162
165
165
167
153
154
159
155
160
164
158
162
160
165
李明
丁阳
李明呈稳中上升趋势,丁阳虽总体呈上升趋势但不够稳定;
(2)李明和丁阳
第5天的成绩相
差多少?
(3)李明和丁阳
跳绳的成绩呈什
么变化趋势?谁
的进步更大?
(4)你能预测两人的比赛成绩吗?
160-157=3(次/分)
167-152=15(次/分)
165-153=12(次/分)
李明进步更大
言之有理
你有哪些收获?
学习目标
1.认识单式折线统计图和复式折线统计图及其特征,能根据需要选择折线统计图直观、有效地表示数据,并能对数据进行简单的分析和预测。
2.经历根据折线统计图解决简单实际问题的过程,掌握对简单数据进行分析的方法。
3.通过对数据的分析,体会统计在生活中的作用和意义,提高数学学习兴趣。
谢谢!
折线统计图整理与复习
学习目标
1.认识单式折线统计图和复式折线统计图及其特征,能根据需要选择折线统计图直观、有效地表示数据,并能对数据进行简单的分析和预测。
2.经历根据折线统计图解决简单实际问题的过程,掌握对简单数据进行分析的方法。
3.通过对数据的分析,体会统计在生活中的作用和意义,提高数学学习兴趣。
条形统计图的特点:
可以清楚的看出数量的多少,
也可以反映出数据的变化情况。
390
0
400
410
420
430
440
450
460
470
480
490
500
510
520
2006
2007
2008
2009
2010
2011
2012
年份
参赛队伍/支
426
394
468
454
489
499
519
中国青少年机器人大赛参赛队伍统计图
(2006—2012年)
折线统计图
单式
折线统计图不仅能够通过点的高低反映数据的多少,还能通过线的起伏反映数据的增减变化,能从中发现数量的变化趋势,并能对将来的发展趋势进行预测。
折线统计图的特点:
中国青少年机器人大赛参赛队伍统计图
(2006—2012年)
390
0
400
410
420
430
440
450
460
470
480
490
500
510
520
2006
2007
2008
2009
2010
2011
2012
年份
参赛队伍/支
426
394
468
454
489
499
519
折线统计图
单式
根据统计表画出折线统计图
年龄/岁
0
1
2
3
4
5
6
7
8
9
10
身高/厘米
50
74
85
93
101
108
115
120
130
135
141
陈东0 ~10岁的身高情况统计表
0
陈东0~10岁身高情况统计图
身高/厘米
50
60
70
80
90
100
110
120
130
140
150
0
1
2
3
4
年龄/岁
5
6
7
8
9
10
50
74
85
93
101
108
115
120
130
135
141
省略
1.描点并标注数据;
2.用线段依次连接各点。
年龄/岁
0
1
2
3
4
5
6
7
8
9
10
身高/厘米
50
74
85
93
101
108
115
120
130
135
141
人数/人
类型
类型
人数/人
20
20
35
25
20
15
40
30
把下面两个统计图合并为复式条形统计图:
人数/人
类型
20
20
35
25
20
15
40
30
复式条形统计图不仅能看出数量的多少,还便于比较两组数据的多少。
5.5
0
6.0
6.5
7.0
7.5
8.0
8.5
9.0
9.5
10.0
10.5
2001
2002
2003
2004
2005
2006
2007
年份
人口数/万人
2008
2009
2010
11.0
6.20
5.73
8.09
8.25
8.12
10.08
9.67
9.23
5.76
10.02
2001-2010年上海出生人口数统计图
5.5
0
6.0
6.5
7.0
7.5
8.0
8.5
9.0
9.5
10.0
10.5
2001
2002
2003
2004
2005
2006
2007
年份
2008
2009
2010
11.0
人口数/万人
2001-2010年上海死亡人口数统计图
9.67
10.07
9.65
10.23
9.80
10.22
10.70
10.67
9.34
10.87
5.5
0
6.0
6.5
7.0
7.5
8.0
8.5
9.0
9.5
10.0
10.5
2001
2002
2003
2004
2005
2006
2007
年份
人口数/万人
2008
2009
2010
11.0
6.20
5.73
8.09
8.25
8.12
10.08
9.67
9.23
5.76
10.02
2001-2010年上海出生人口和死亡人口数统计图
9.67
10.07
9.65
10.23
9.80
10.22
10.70
10.67
9.34
10.87
出生人口
死亡人口
5.5
0
6.0
6.5
7.0
7.5
8.0
8.5
9.0
9.5
10.0
10.5
2001
2002
2003
2004
2005
2006
2007
年份
人口数/万人
2008
2009
2010
11.0
6.20
5.73
8.09
8.25
8.12
10.08
9.67
9.23
5.76
10.02
9.67
10.07
9.65
10.23
9.80
10.22
10.70
10.67
9.34
10.87
2001-2010年上海出生人口和死亡人口数统计图
出生人口
死亡人口
绘制复式折线统计图与单式折线统计图的步骤相同,按数据描出各点并标明数据,用线段依次连接各点,
在一个统计图里,用两条或两条以上折线分别表示两条不同的数据,这样的折线统计图叫做复式折线统计图。
用图例标明两条折线的含义。
复式折线统计图不仅能看出数量增减变化的情况,而且便于比较出两组数据的差异和变化趋势。
①描点 ②标数 ③连线 ④标图例
5.5
0
6.0
6.5
7.0
7.5
8.0
8.5
9.0
9.5
10.0
10.5
2001
2002
2003
2004
2005
2006
2007
年份
人口数/万人
2008
2009
2010
11.0
6.20
5.73
8.09
8.25
8.12
10.08
9.67
9.23
5.76
10.02
9.67
10.07
9.65
10.23
9.80
10.22
10.70
10.67
9.34
10.87
2001-2010年上海出生人口和死亡人口数统计图
出生人口
死亡人口
39
38
37
36
0
6
时间/时
体温/℃
12
18
0
6
12
18
0
6
39.5
37.1
38
39.2
38
37
36.8
37.2
一个病人住院期间体温变化情况统计图
18
12
5月23日
5月24日
5月25日
1.根据统计图回答问题。
(5)从体温上看,这位病人的病情是在恶化还是在好转?
为什么?
(1)护士每 小时给病人测一次体温。
(2)这位病人体温最高是 ℃,最低是 ℃。
(3)病人在5月24日12时
的体温是 。
(4)图中虚线表示 。
6
39.5
36.8
37.5℃
人的正常体温
好转
因为体温趋于正常
2.
2000年最多,
2010年最少。
2002年最多,
2010年最少。
从整体上看,学龄儿童人数和入学人数都在逐年减少,并且越来越接近,说明学龄儿童入学率在稳步提高。
11310.4-11150.0=160.4(万人)
9501.5-9473.3=28.2(万人)
没上学人数=学龄儿童人数-入学人数
销售量/台
0
30
35
40
45
50
55
60
65
70
80
85
1
2
3
4
时间/月
5
6
7
8
9
10
11
12
75
70
80
40
甲、乙两种品牌空调2019年销售情况统计图
61
54
41
38
42
46
35
46
60
75
39
38
41
50
46
50
84
39
42
52
55
甲品牌
乙品牌
3.
14
25
(40+39+38+41+50+46+39+42+50+52+55+84)÷12=48(台)
(1)乙品牌空调从( )
月到( )月的销售量
上升最快。
(2)从2月到6月,( )
品牌空调的销售量呈下
降趋势。
(3)乙品牌空调平均每
月销售( )台。
(4)甲品牌空调7月份销售量是12月份的(——),
乙品牌空调1月份的销售量是5月份的(——)。
11
12
甲
48
42
75
40
50
4
5
4.李明和丁阳参加学校运动会一分钟跳绳比赛,提前十天进行训练,每天测试成绩如下表。(单位:次)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
1
2
3
4
5
6
7
8
9
10
李明
152
155
158
160
157
159
162
165
165
167
丁阳
153
154
159
155
160
164
158
162
160
165
第几
天
成
绩
(次
/分)
姓名
(1)根据表中数据完成统计图。
150
0
152
154
156
158
160
162
164
166
168
170
1
2
3
4
5
6
7
时间/天
8
9
10
172
成绩 /(次/分)
李明、丁阳一分钟跳绳情况统计图
152
155
158
160
157
159
162
165
165
167
153
154
159
155
160
164
158
162
160
165
李明
丁阳
李明呈稳中上升趋势,丁阳虽总体呈上升趋势但不够稳定;
(2)李明和丁阳
第5天的成绩相
差多少?
(3)李明和丁阳
跳绳的成绩呈什
么变化趋势?谁
的进步更大?
(4)你能预测两人的比赛成绩吗?
160-157=3(次/分)
167-152=15(次/分)
165-153=12(次/分)
李明进步更大
言之有理
你有哪些收获?
学习目标
1.认识单式折线统计图和复式折线统计图及其特征,能根据需要选择折线统计图直观、有效地表示数据,并能对数据进行简单的分析和预测。
2.经历根据折线统计图解决简单实际问题的过程,掌握对简单数据进行分析的方法。
3.通过对数据的分析,体会统计在生活中的作用和意义,提高数学学习兴趣。
谢谢!
