人教版数学五年级下册第三单元 复习与整理 课件(46张ppt)
文档属性
| 名称 | 人教版数学五年级下册第三单元 复习与整理 课件(46张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 578.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 00:00:00 | ||
图片预览


文档简介
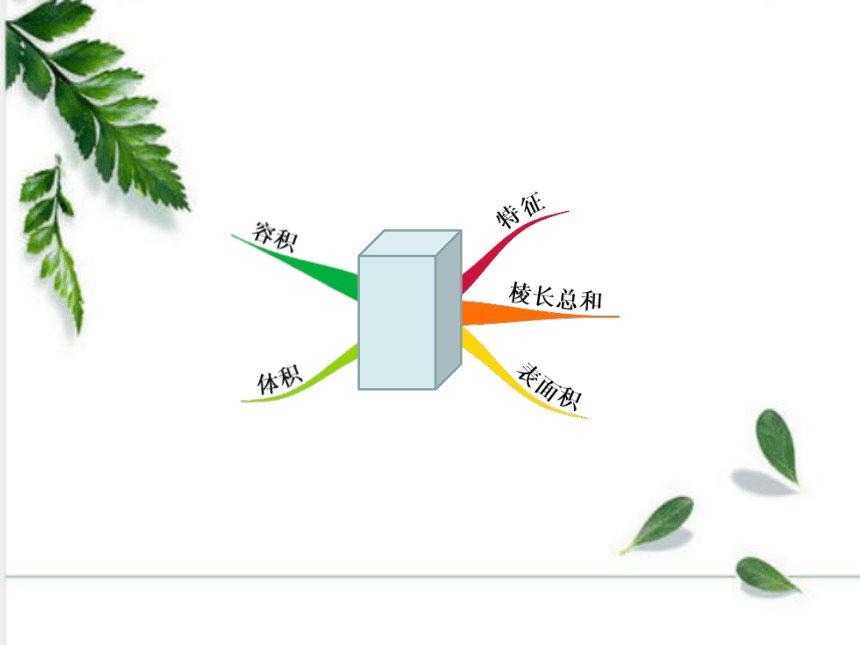
长方体和正方体的整理与复习
人教版小学数学五年级 第三单元
学习目标
2.在整理长方体和正方体相关知识的过程中,培养对所学知识归纳、整理的能力。
3.在解决实际问题的过程中,感受数学在生活中的作用,并进一步培养空间观念。
1.进一步掌握长方体和正方体的特征、表面积、体积的有关知识以及相邻单位间的进率,并能够正确完成相关计算。
面、棱、顶点
长方体的特征
回顾:长方体有哪几个面?每个面是什么形状的?
长方体的特征
后面
下面(底面)
左面
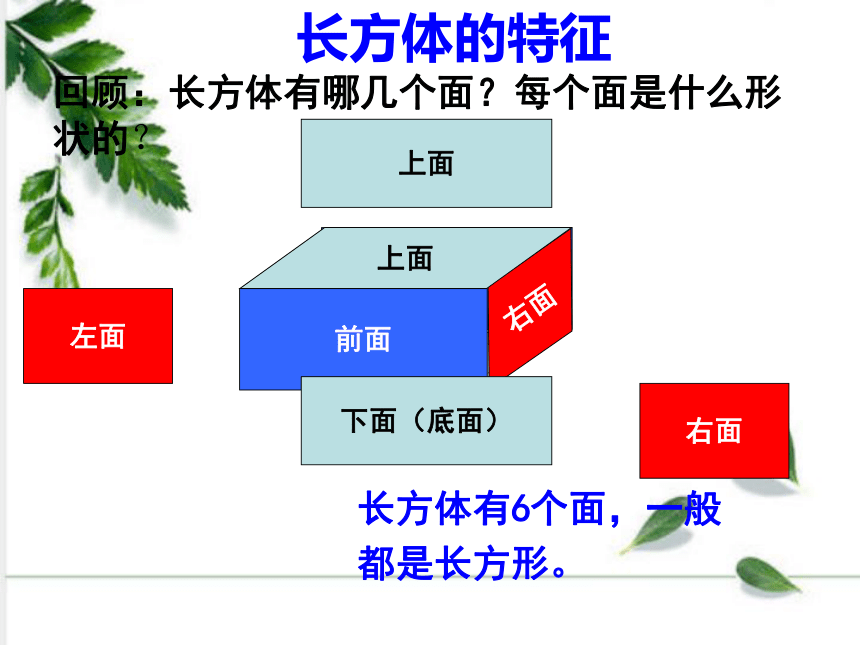
回顾:长方体有哪几个面?每个面是什么形状的?
长方体的特征
右面
上面
前面
长方体有6个面,一般
都是长方形。
上面
右面
下面(底面)
左面
后面
下面(底面)
左面
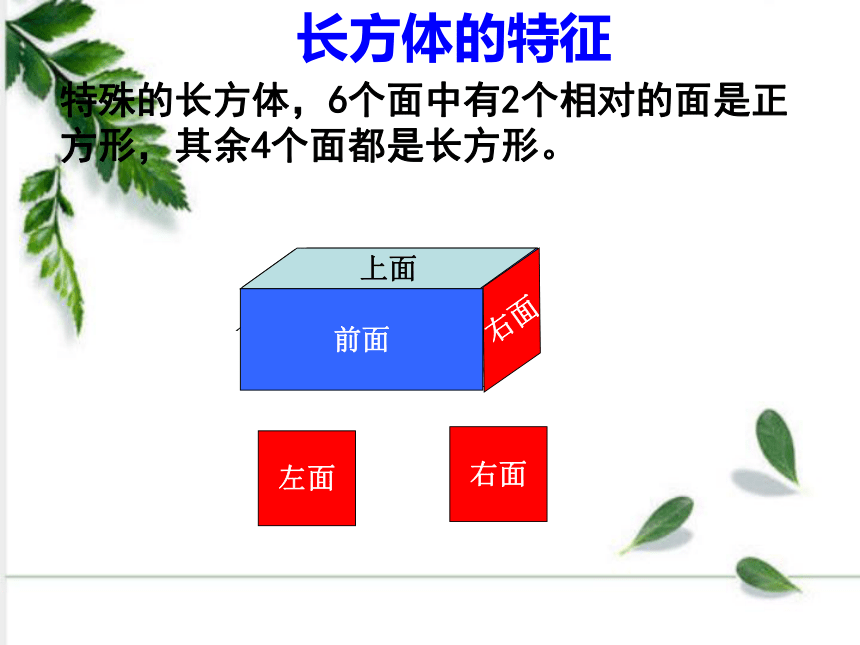
特殊的长方体,6个面中有2个相对的面是正方形,其余4个面都是长方形。
长方体的特征
右面
上面
前面
左面
右面
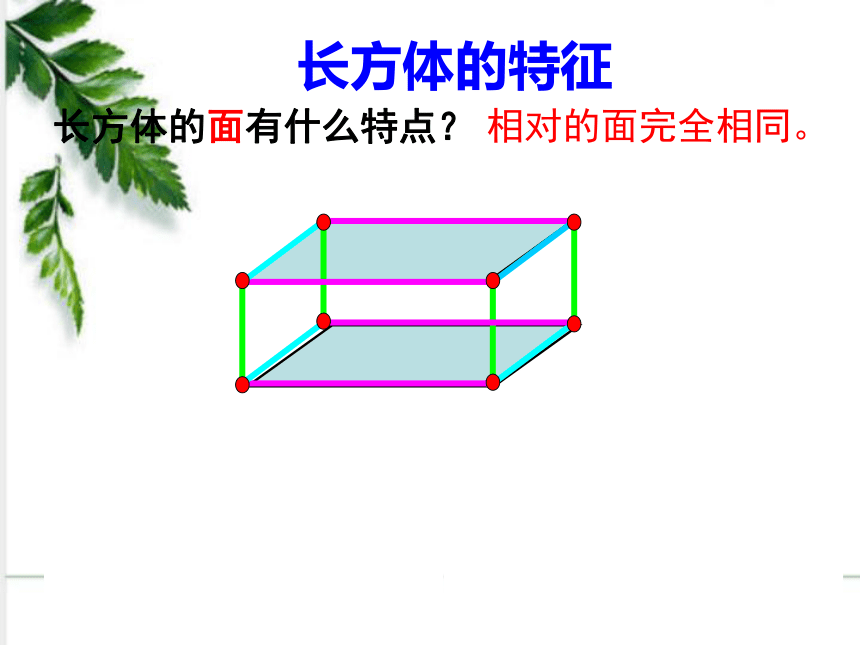
长方体的面有什么特点?
长方体的特征
相对的面完全相同。
长方体的特征
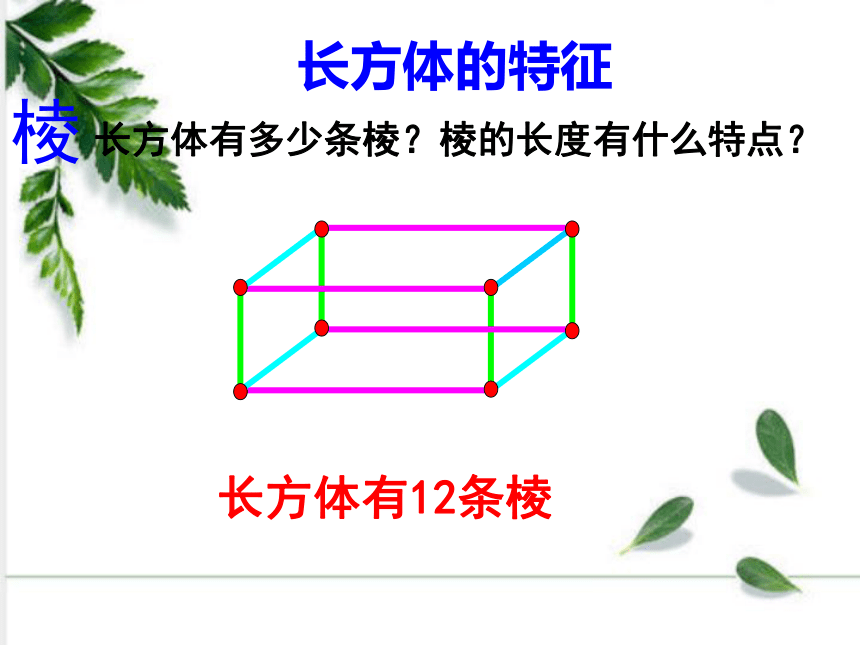
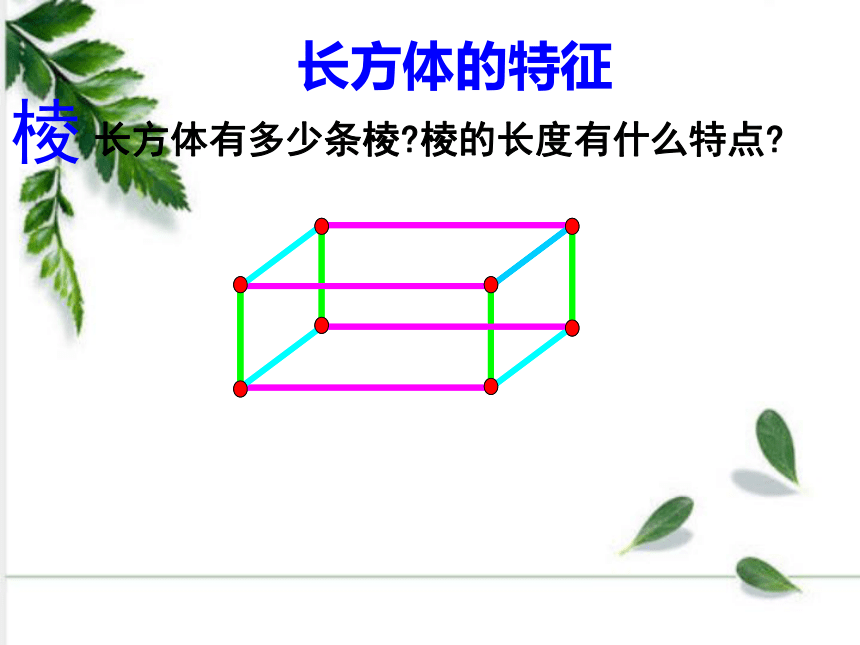
长方体有多少条棱?棱的长度有什么特点?
长方体有12条棱
棱
长方体的特征
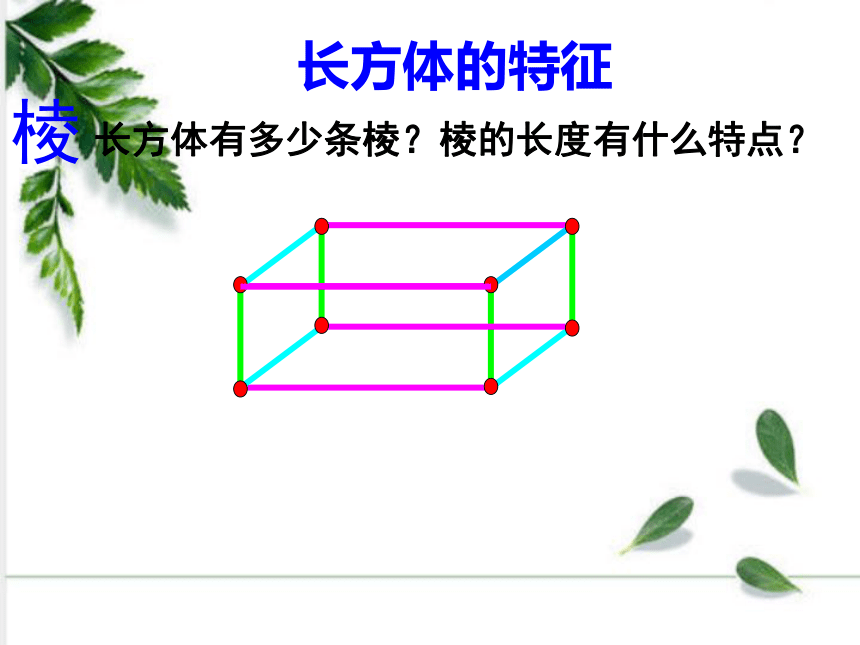
长方体有多少条棱?棱的长度有什么特点?
棱
长方体的特征
长方体有多少条棱?棱的长度有什么特点?
棱
长方体的特征
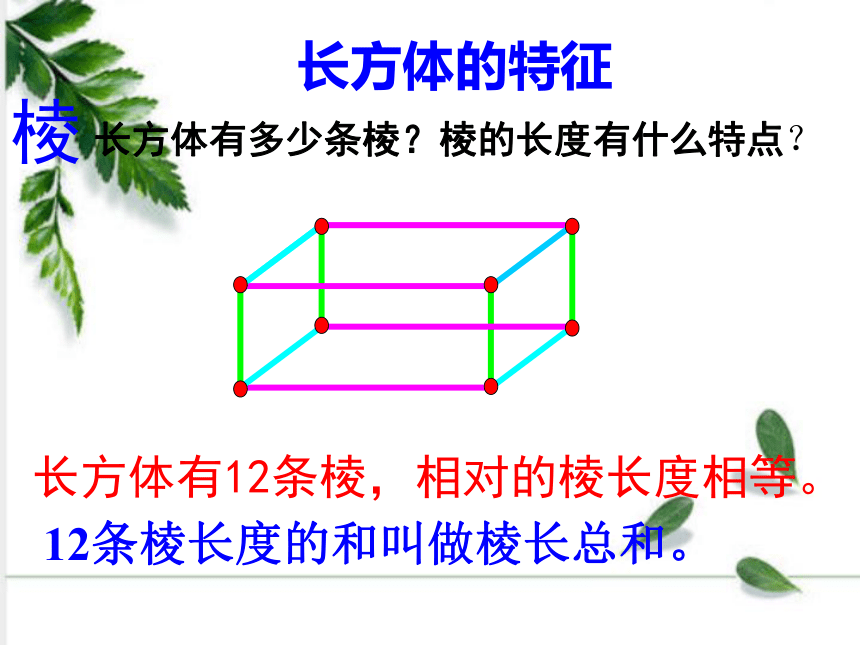
长方体有多少条棱?棱的长度有什么特点?
长方体有12条棱,相对的棱长度相等。
12条棱长度的和叫做棱长总和。
棱
相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
长
宽
高
12条棱可以分成4组长、宽、高。
棱长总和=(长+宽+高)×4
·
顶点
长方体的特征
共有8个。
三条棱相交的点,
正方体的特征:
面
棱
顶点
6个
12条
长度都相等
8个
棱长总和=棱长×12
完全相同的正方形
长方体
长方体与正方体的关系
正方体
正方体是长、宽、高都相等的长方体。
什么叫长方体、正方体的表面积?
6个面的总面积,叫做它们的表面积。
上
右
前
长方体的表面积怎样计算?
前
上
下
左
右
后
上下面:长×宽×2
前后面:长×高×2
左右面:宽×高×2
S表=长×宽×2+长×高×2+宽×高× 2
S表=(长×宽+长×高+宽×高)× 2
长
高
宽
宽
长
高
S表=2ab+2ah+ 2bh
S表=(ab+ah+bh)× 2
上
前
后
正方体的表面积怎样计算?
上
下
左
右
前
后
S表=棱长 ×棱长×6
6个面的面积都相等,都等于棱长×棱长。
S表=6a2
在计算下列物体面积时,应考虑几个面?
(2)粉刷教室的四壁和房顶。
(3)通风管道。
(4)给礼堂内长方体柱子刷漆。
5个面
4个面
4个面
(1)制作一个无盖的长方体铁皮桶的用料。
5个面
(5)长方体油桶用料。
6个面
1.什么叫做体积?
物体所占空间的大小叫做物体的体积。
2.常用的体积单位有哪些?
立方厘米(cm3)
立方分米(dm3)
立方米 ( m3)
每相邻体积单位之间的进率都是1000.
回顾:长方体、正方体的体积公式?
长方体的体积=长×宽×高
V=abh
底面
正方体的体积=棱长×棱长×棱长
V=a3
V=Sh
底面
容器所能容纳物体的体积叫做容积。
常见的容积单位有:
升(L)、毫升(ml)
进率是1000.
什么叫做容积?
1L=1000mL
计量容积一般用体积单位cm3 dm3 和m3,
计量液体的体积常用容积单位升和毫升,
容积单位与体积单位之间的关系:
1L=1dm3 1mL=1cm3
容积与体积的异同点:
相同点:计算方法
不同点:计算体积从外面量长宽高,
计算容积从里面量长宽高。
1.(1)一个长方体被切割成两个小长方体,
它的表面积和体积都没有改变。( )
(2)一个长方体,长、宽、高都扩大2倍,
体积也扩大2倍。( )
(3)长方体的体积也可以用底面积
乘以高求得。 ( )
1.(1)一个长方体被切割成两个小长方体,它的表面积和体积都没有改变。( )
×
多了2个面
1.(1)一个长方体被切割成两个小长方体,
它的表面积和体积都没有改变。( )
×
(2)一个长方体,长、宽、高都扩大2倍,
体积也扩大2倍。( )
2cm
1cm
3cm
2 × 1 × 3
= 2 × 3
= 6( cm3 )
4cm
2cm
6cm
4 × 2 × 6
= 8 × 6
= 48( cm3 )
8
1.(1)一个长方体被切割成两个小长方体,
它的表面积和体积都没有改变。( )
?
×
(2)一个长方体,长、宽、高都扩大2倍,
体积也扩大2倍。( )
×
(3)长方体的体积也可以用底面积
乘以高求得。 ( )
2.小卖部要做一个长方体的无盖玻璃柜台,长是6m,宽是60cm,高是1.5m。
(2)柜台的占地面积有多大?
(3)至少需要多少平方米的玻璃?
(4)它的体积是多少?
(1)要在柜台各边都按上角铁,至少需要多少米的角铁?
2.小卖部要做一个长方体的无盖玻璃柜台,长是 ,宽是 ,高是 。
6m 60cm 1.5m
统一单位
2.小卖部要做一个长方体的无盖玻璃柜台,长是6m,宽是60cm,高是1.5m。
(1)要在柜台各边都按上角铁,至少需要多少米的角铁?
长方体的棱长总和
60cm=0.6m
(6+0.6+1.5)×4
=8.1×2
=32.4(m)
答:至少需要32.4米的角铁。
2.小卖部要做一个长方体的无盖玻璃柜台,长是6m,宽是60cm,高是1.5m。
(2)柜台的占地面积有多大?
底面积
6×0.6=3.6(m?)
答:柜台的占地面积是3.6平方米。
2.小卖部要做一个长方体的 玻璃柜台,长是6m,宽是60cm,高是1.5m。
(3)至少需要多少平方米的玻璃?
5个面的面积
无盖
=3.6+(9+0.9)×2
=3.6+9.9×2
=3.6+19.8
=23.4(m?)
答:至少需要23.4平方米的玻璃。
6×0.6+(6×1.5+0.6×1.5)×2
2.小卖部要做一个长方体的无盖玻璃柜台,长是6m,宽是60cm,高是1.5m。
(4)它的体积是多少?
体积=底面积×高
3.6×1.5=5.4(m?)
答:它的体积是5.4立方米。
3.一个长方体容器,底面长2dm,宽1.5dm,将一个土豆完全浸没在水中,水面升高了0.2dm,这个土豆的体积是多少?
2×1.5×0.2
=3×0.2
=0.6(dm3)
答:这个土豆的体积是0.6立方分米。
土豆的体积=上升的水的体积
4.把一个长方体木料长4m,如图截成三个一样大的小长方体,表面积增加60dm2,求原来长方体的体积是多少立方分米?
=15×40
=600(立方分米)
4m
4m=40dm
60÷4
×40
答:原来长方体的体积是600立方分米。
学习目标
2.在整理长方体和正方体相关知识的过程中,培养对所学知识归纳、整理的能力。
3.在解决实际问题的过程中,感受数学在生活中的作用,并进一步培养空间观念。
1.进一步掌握长方体和正方体的特征、表面积、体积的有关知识以及相邻单位间的进率,并能够正确完成相关计算。
(长+宽+高)×4
棱长×12
当机会来了,你能不能抓得住,其实就靠平时的积累。
人教版小学数学五年级 第三单元
学习目标
2.在整理长方体和正方体相关知识的过程中,培养对所学知识归纳、整理的能力。
3.在解决实际问题的过程中,感受数学在生活中的作用,并进一步培养空间观念。
1.进一步掌握长方体和正方体的特征、表面积、体积的有关知识以及相邻单位间的进率,并能够正确完成相关计算。
面、棱、顶点
长方体的特征
回顾:长方体有哪几个面?每个面是什么形状的?
长方体的特征
后面
下面(底面)
左面
回顾:长方体有哪几个面?每个面是什么形状的?
长方体的特征
右面
上面
前面
长方体有6个面,一般
都是长方形。
上面
右面
下面(底面)
左面
后面
下面(底面)
左面
特殊的长方体,6个面中有2个相对的面是正方形,其余4个面都是长方形。
长方体的特征
右面
上面
前面
左面
右面
长方体的面有什么特点?
长方体的特征
相对的面完全相同。
长方体的特征
长方体有多少条棱?棱的长度有什么特点?
长方体有12条棱
棱
长方体的特征
长方体有多少条棱?棱的长度有什么特点?
棱
长方体的特征
长方体有多少条棱?棱的长度有什么特点?
棱
长方体的特征
长方体有多少条棱?棱的长度有什么特点?
长方体有12条棱,相对的棱长度相等。
12条棱长度的和叫做棱长总和。
棱
相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
长
宽
高
12条棱可以分成4组长、宽、高。
棱长总和=(长+宽+高)×4
·
顶点
长方体的特征
共有8个。
三条棱相交的点,
正方体的特征:
面
棱
顶点
6个
12条
长度都相等
8个
棱长总和=棱长×12
完全相同的正方形
长方体
长方体与正方体的关系
正方体
正方体是长、宽、高都相等的长方体。
什么叫长方体、正方体的表面积?
6个面的总面积,叫做它们的表面积。
上
右
前
长方体的表面积怎样计算?
前
上
下
左
右
后
上下面:长×宽×2
前后面:长×高×2
左右面:宽×高×2
S表=长×宽×2+长×高×2+宽×高× 2
S表=(长×宽+长×高+宽×高)× 2
长
高
宽
宽
长
高
S表=2ab+2ah+ 2bh
S表=(ab+ah+bh)× 2
上
前
后
正方体的表面积怎样计算?
上
下
左
右
前
后
S表=棱长 ×棱长×6
6个面的面积都相等,都等于棱长×棱长。
S表=6a2
在计算下列物体面积时,应考虑几个面?
(2)粉刷教室的四壁和房顶。
(3)通风管道。
(4)给礼堂内长方体柱子刷漆。
5个面
4个面
4个面
(1)制作一个无盖的长方体铁皮桶的用料。
5个面
(5)长方体油桶用料。
6个面
1.什么叫做体积?
物体所占空间的大小叫做物体的体积。
2.常用的体积单位有哪些?
立方厘米(cm3)
立方分米(dm3)
立方米 ( m3)
每相邻体积单位之间的进率都是1000.
回顾:长方体、正方体的体积公式?
长方体的体积=长×宽×高
V=abh
底面
正方体的体积=棱长×棱长×棱长
V=a3
V=Sh
底面
容器所能容纳物体的体积叫做容积。
常见的容积单位有:
升(L)、毫升(ml)
进率是1000.
什么叫做容积?
1L=1000mL
计量容积一般用体积单位cm3 dm3 和m3,
计量液体的体积常用容积单位升和毫升,
容积单位与体积单位之间的关系:
1L=1dm3 1mL=1cm3
容积与体积的异同点:
相同点:计算方法
不同点:计算体积从外面量长宽高,
计算容积从里面量长宽高。
1.(1)一个长方体被切割成两个小长方体,
它的表面积和体积都没有改变。( )
(2)一个长方体,长、宽、高都扩大2倍,
体积也扩大2倍。( )
(3)长方体的体积也可以用底面积
乘以高求得。 ( )
1.(1)一个长方体被切割成两个小长方体,它的表面积和体积都没有改变。( )
×
多了2个面
1.(1)一个长方体被切割成两个小长方体,
它的表面积和体积都没有改变。( )
×
(2)一个长方体,长、宽、高都扩大2倍,
体积也扩大2倍。( )
2cm
1cm
3cm
2 × 1 × 3
= 2 × 3
= 6( cm3 )
4cm
2cm
6cm
4 × 2 × 6
= 8 × 6
= 48( cm3 )
8
1.(1)一个长方体被切割成两个小长方体,
它的表面积和体积都没有改变。( )
?
×
(2)一个长方体,长、宽、高都扩大2倍,
体积也扩大2倍。( )
×
(3)长方体的体积也可以用底面积
乘以高求得。 ( )
2.小卖部要做一个长方体的无盖玻璃柜台,长是6m,宽是60cm,高是1.5m。
(2)柜台的占地面积有多大?
(3)至少需要多少平方米的玻璃?
(4)它的体积是多少?
(1)要在柜台各边都按上角铁,至少需要多少米的角铁?
2.小卖部要做一个长方体的无盖玻璃柜台,长是 ,宽是 ,高是 。
6m 60cm 1.5m
统一单位
2.小卖部要做一个长方体的无盖玻璃柜台,长是6m,宽是60cm,高是1.5m。
(1)要在柜台各边都按上角铁,至少需要多少米的角铁?
长方体的棱长总和
60cm=0.6m
(6+0.6+1.5)×4
=8.1×2
=32.4(m)
答:至少需要32.4米的角铁。
2.小卖部要做一个长方体的无盖玻璃柜台,长是6m,宽是60cm,高是1.5m。
(2)柜台的占地面积有多大?
底面积
6×0.6=3.6(m?)
答:柜台的占地面积是3.6平方米。
2.小卖部要做一个长方体的 玻璃柜台,长是6m,宽是60cm,高是1.5m。
(3)至少需要多少平方米的玻璃?
5个面的面积
无盖
=3.6+(9+0.9)×2
=3.6+9.9×2
=3.6+19.8
=23.4(m?)
答:至少需要23.4平方米的玻璃。
6×0.6+(6×1.5+0.6×1.5)×2
2.小卖部要做一个长方体的无盖玻璃柜台,长是6m,宽是60cm,高是1.5m。
(4)它的体积是多少?
体积=底面积×高
3.6×1.5=5.4(m?)
答:它的体积是5.4立方米。
3.一个长方体容器,底面长2dm,宽1.5dm,将一个土豆完全浸没在水中,水面升高了0.2dm,这个土豆的体积是多少?
2×1.5×0.2
=3×0.2
=0.6(dm3)
答:这个土豆的体积是0.6立方分米。
土豆的体积=上升的水的体积
4.把一个长方体木料长4m,如图截成三个一样大的小长方体,表面积增加60dm2,求原来长方体的体积是多少立方分米?
=15×40
=600(立方分米)
4m
4m=40dm
60÷4
×40
答:原来长方体的体积是600立方分米。
学习目标
2.在整理长方体和正方体相关知识的过程中,培养对所学知识归纳、整理的能力。
3.在解决实际问题的过程中,感受数学在生活中的作用,并进一步培养空间观念。
1.进一步掌握长方体和正方体的特征、表面积、体积的有关知识以及相邻单位间的进率,并能够正确完成相关计算。
(长+宽+高)×4
棱长×12
当机会来了,你能不能抓得住,其实就靠平时的积累。
