2020-2021学年七年级数学下册《5.2 平行线及其判定》课时练习(Word版 含解析)
文档属性
| 名称 | 2020-2021学年七年级数学下册《5.2 平行线及其判定》课时练习(Word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 179.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 00:00:00 | ||
图片预览


文档简介
2020-2021学年七年级数学下册《5.2 平行线及其判定》课时练习
一、选择题
1.在同一平面内,不重合的两条直线的位置关系是( ).
A.平行 B.相交 C.平行或相交 D.平行或垂直
2. 在同一平面内三条不同的直线a、b、c,其中a⊥b,a⊥c,则直线b与直线c的关系是( )
A.相交 B.平行 C.垂直 D.不确定
3.如图,直线a,b被直线c所截,下列条件能判断a∥b的是( )
A.∠3=∠5 B.∠4=∠7
C.∠2+∠3=180° D.∠1=∠3
4.如果线段AB与线段CD没有交点,则( )
A.线段AB与线段CD一定平行
B.线段AB与线段CD一定不平行
C.线段AB与线段CD可能平行
D.以上说法都不正确
5.下列说法错误的是( )
A.在同一平面内,不相交的两条线段必然平行
B.在同一平面内,不相交的两条直线必然平行
C.在同一平面内,不平行的两条线段延长后必然相交
D.在同一平面内,两条直线没有公共点,那么两条直线平行
6.如图,“因为false,所以false”,其推导的依据是( )
A.两直线平行,同位角相等 B.两直线平行,内错角相等
C.同位角相等,两直线平行 D.内错角相等,两直线平行
7.在同一平面内有三条直线,如果要使其中两条且只有两条直线平行,那么它们( )
A.没有交点 B.只有一个交点
C.有两个交点 D.有三个交点
8.下列语句中,正确的个数有( )
①同位角相等,两直线平行; ②若两个角的和为180°,则这两个角互补;
③同旁内角相等,两直线平行; ④内错角相等,两直线平行.
A.4个 B.3个 C.2个 D.1个
9.如图,下列不能判定DF∥AC的条件是( )
A.∠A=∠BDF B.∠2=∠4
C.∠1=∠3 D.∠A+∠ADF=180°
10.如图是嘉淇证明“在同一平面内,垂直于同一条直线的两条直线平行”的过程,下列判断不正确的是( )
证明:在同一平面内,垂直于同一条直线的两条直线平行,
已知:如图,直线false,false,false,false,false.
求证: △ .
证明:false(已知),
false(垂直的定义).
false □ (已知).
false(垂直的定义),
false ○ (等量代换),
false( ◇ )
A.△代表false B.□代表false
C.○代表false D.◇代表两直线平行,同位角相等
二、填空题
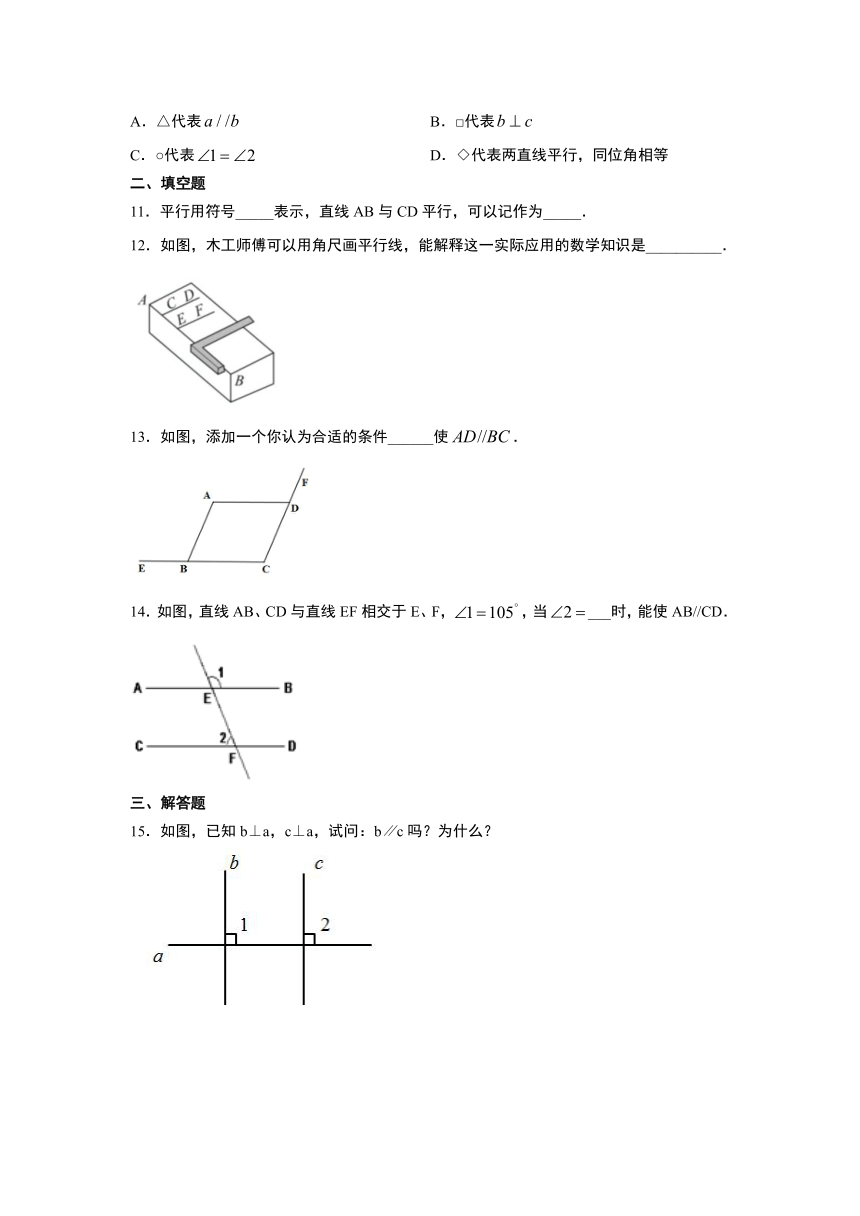
11.平行用符号_____表示,直线AB与CD平行,可以记作为_____.
12.如图,木工师傅可以用角尺画平行线,能解释这一实际应用的数学知识是__________.
13.如图,添加一个你认为合适的条件______使false.
14.如图,直线AB、CD与直线EF相交于E、F,false,当false___时,能使AB//CD.
三、解答题
15.如图,已知b⊥a,c⊥a,试问:b∥c吗?为什么?
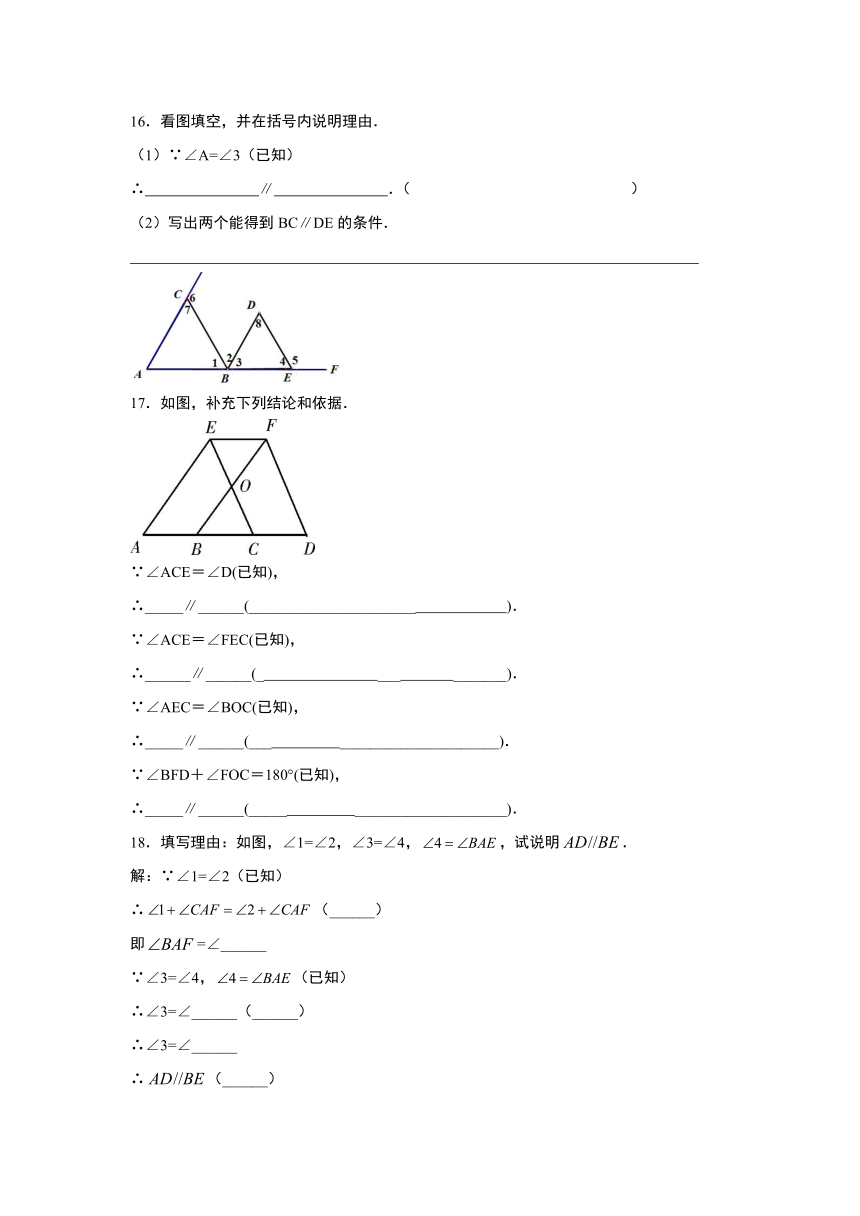
16.看图填空,并在括号内说明理由.
(1)∵∠A=∠3(已知)
∴ ∥ .( )
(2)写出两个能得到BC∥DE的条件.
17.如图,补充下列结论和依据.
∵∠ACE=∠D(已知),
∴_____∥______(______________________ ).
∵∠ACE=∠FEC(已知),
∴______∥______(_ ___ _______).
∵∠AEC=∠BOC(已知),
∴_____∥______(___ _____________________).
∵∠BFD+∠FOC=180°(已知),
∴_____∥______(_____ ____________________).
18.填写理由:如图,∠1=∠2,∠3=∠4,false,试说明false.
解:∵∠1=∠2(已知)
∴false(______)
即false=∠______
∵∠3=∠4,false(已知)
∴∠3=∠______(______)
∴∠3=∠______
∴false(______)
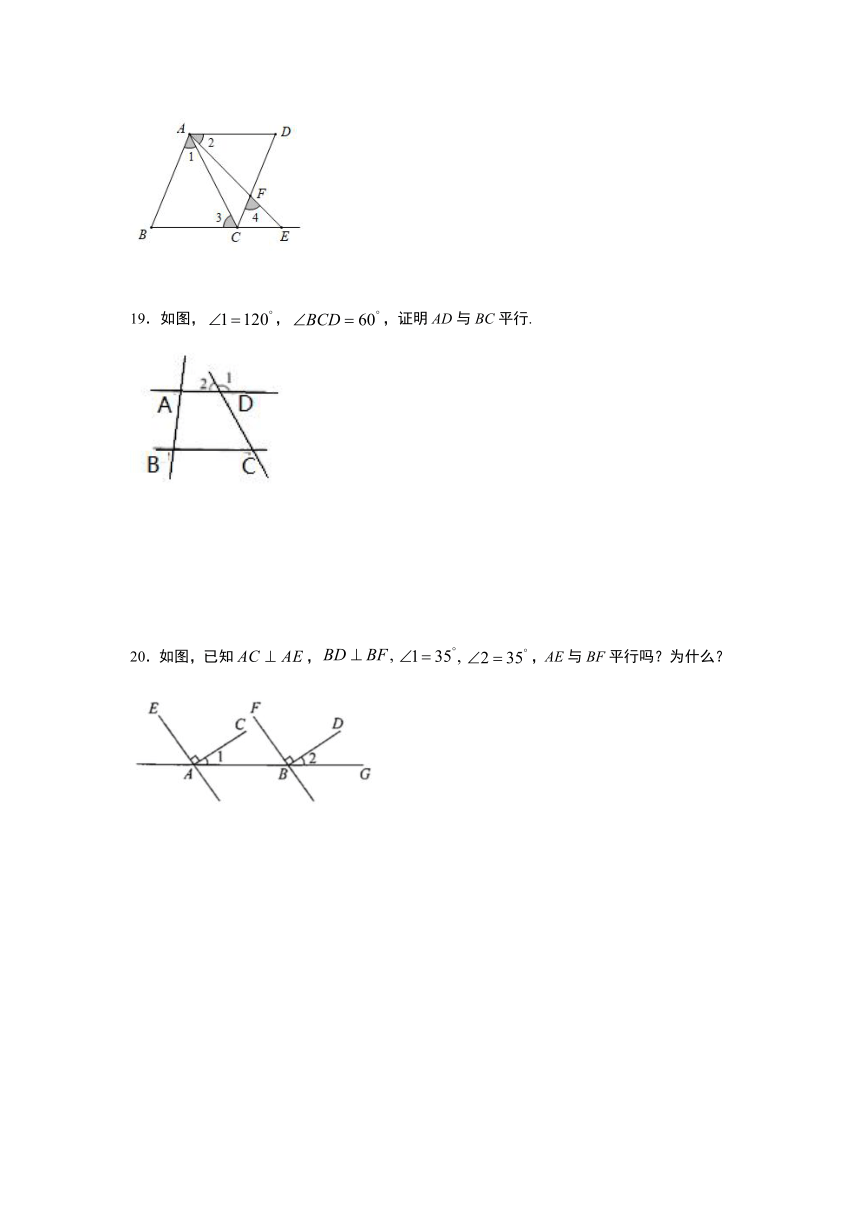
19.如图,false,false,证明AD与BC平行.
20.如图,已知false,falsefalsefalse,AE与BF平行吗?为什么?
参考答案
一、选择题
1.C
解:在同一平面内,不重合的两条直线的位置关系是相交或平行,相交包含垂直.
2.B
解:∵a⊥b,a⊥c
∴a∥c.
3.A
解:A选项,
∵∠3=∠5(已知),
∴a∥b(内错角相等,两直线平行).
B选项,∠4=∠7,∠4与∠7无关系,不能判定平行;
C选项,∠2+∠3=180°,∠2与∠3为邻补角,不能判定平行;
D选项,∠1=∠3,∠1与∠3为对顶角,不能判定两直线平行;
4.C
解:A选项,线段AB与线段CD不一定平行,如下图所示,故本选项错误;
B选项,线段AB与线段CD不一定不平行,有可能平行,故本选项错误;
C选项,线段AB与线段CD可能平行,故本选项正确;
D选项,C选项说法正确,故本选项错误.
5.A
在同一平面内,不相交的两条直线必然平行; 在同一平面内,不平行的两条线段延长后必然相交; 在同一平面内,两条直线没有公共点,那么两条直线平行;只有A选项中, 在同一平面内,不相交的两条线段不一定平行,故A错误.
6.D
解:∵∠2和∠4是内错角,
∴根据“内错角相等,两直线平行”可得AD∥BC,
7.C
解:根据题意,第三条直线与这两条平行直线各有一个交点.
8.B
解:①同位角相等,两直线平行,故正确;
②若两个角的和为180°,则这两个角互补,故正确;
③同旁内角互补,两直线平行,故错误;
④内错角相等,两直线平行,故正确.
综上可得①②④正确.
9.B
解:A.∠A=∠BDF,由同位角相等,两直线平行,可判断DF∥AC;
B.∠2=∠4,不能判断DF∥AC;
C.∠1=∠3由内错角相等,两直线平行,可判断DF∥AC;
D.∠A+∠ADF=180°,由同旁内角互补,两直线平行,可判断DF∥AC;
10.D
解:在同一平面内,垂直于同一条直线的两条直线平行,
已知:如图,直线a,b,c,a⊥c,b⊥c.求证:a//b .
解:∵a⊥c(已知),
∴∠1=90°(垂直的定义).
∵b⊥c (已知).
∴∠2=90°(垂直的定义),
∴∠1=∠2 (等量代换),
∴a//b( 同位角相等,两直线平行)
A,△代表 a//b,故A正确,
B,□代表 b⊥c,故B正确,
C,○代表 ∠1=∠2,故C正确,
D,◇代表 同位角相等,两直线平行,故D不正确.
二、填空题
11.∥ AB∥CD
解:平行用符号∥表示,直线AB与CD平行,可以记作为AB∥CD.
12.在同一平面内,垂直于同一条直线的两条直线平行或根据同位角相等两直线平行.
解:如图:∵CD⊥AB,EF⊥AB,
∴CD//EF(在同一平面内,垂直于同一条直线的两条直线平行)
或∵∠ACD=∠AEF=90°,
∴CD//EF(同位角相等两直线平行),
13.∠ADF=∠C或∠A=∠ABE或∠A+∠ABC=180°或∠C+∠ADC=180°(答案不唯一,写一个正确的即可)
第一种情况,同位角相等,两直线平行,即∠ADF=∠C时,false;
第二种情况,内错角相等,两直线平行,即∠A=∠ABE时,false;
第三种情况,同旁内角互补,两直线平行,即∠A+∠ABC=180°或∠C+∠ADC=180°时,false;
14.75°
∵false,
∴false,
要使AB∥CD,则false,
∴false,
三、解答题
15.
解:b∥c,理由如下:
∵b⊥a,c⊥a,
∴∠1=∠2=90°,
∴b∥c(同位角相等,两直线平行).
16.解:
(1)∵∠A=∠3(已知)
∴AC∥BD.(同位角相等,两直线平行)
(2)∠1=∠4;∠2=∠8
因为∠1和∠4是同位角,如果两角相等,那么BC∥DE;
因为∠2和∠8是内错角,如果两角相等,那么BC∥DE.
17.
解:∵∠ACE=∠D(已知),
根据同位角相等两直线平行,
∴CE∥DF.
∵∠ACE=∠FEC,
根据内错角相等,两直线平行,
∴EF∥AD.
∵∠AEC=∠BOC,
根据同位角相等,两直线平行,
∴AE∥BF.
根据∠BFD+∠FOC=180°,
根据同旁内角互补,两直线平行,
∴CE∥DF.
18.解:
∵∠1=∠2(已知)
∴false(等式的性质)
即false=∠ DAC
∵∠3=∠4,false(已知)
∴∠3=∠BAE(等量代换)
∴∠3=∠DAC
∴false(内错角相等,两直线平行)
19.解:
false,且false,
false.
false,
false.
false(同位角相等,两直线平行).
20.解:
false.理由如下:
因为falsefalse,
所以false.
因为false,所以false,
即false.
所以false(同位角相等,两直线平行).
一、选择题
1.在同一平面内,不重合的两条直线的位置关系是( ).
A.平行 B.相交 C.平行或相交 D.平行或垂直
2. 在同一平面内三条不同的直线a、b、c,其中a⊥b,a⊥c,则直线b与直线c的关系是( )
A.相交 B.平行 C.垂直 D.不确定
3.如图,直线a,b被直线c所截,下列条件能判断a∥b的是( )
A.∠3=∠5 B.∠4=∠7
C.∠2+∠3=180° D.∠1=∠3
4.如果线段AB与线段CD没有交点,则( )
A.线段AB与线段CD一定平行
B.线段AB与线段CD一定不平行
C.线段AB与线段CD可能平行
D.以上说法都不正确
5.下列说法错误的是( )
A.在同一平面内,不相交的两条线段必然平行
B.在同一平面内,不相交的两条直线必然平行
C.在同一平面内,不平行的两条线段延长后必然相交
D.在同一平面内,两条直线没有公共点,那么两条直线平行
6.如图,“因为false,所以false”,其推导的依据是( )
A.两直线平行,同位角相等 B.两直线平行,内错角相等
C.同位角相等,两直线平行 D.内错角相等,两直线平行
7.在同一平面内有三条直线,如果要使其中两条且只有两条直线平行,那么它们( )
A.没有交点 B.只有一个交点
C.有两个交点 D.有三个交点
8.下列语句中,正确的个数有( )
①同位角相等,两直线平行; ②若两个角的和为180°,则这两个角互补;
③同旁内角相等,两直线平行; ④内错角相等,两直线平行.
A.4个 B.3个 C.2个 D.1个
9.如图,下列不能判定DF∥AC的条件是( )
A.∠A=∠BDF B.∠2=∠4
C.∠1=∠3 D.∠A+∠ADF=180°
10.如图是嘉淇证明“在同一平面内,垂直于同一条直线的两条直线平行”的过程,下列判断不正确的是( )
证明:在同一平面内,垂直于同一条直线的两条直线平行,
已知:如图,直线false,false,false,false,false.
求证: △ .
证明:false(已知),
false(垂直的定义).
false □ (已知).
false(垂直的定义),
false ○ (等量代换),
false( ◇ )
A.△代表false B.□代表false
C.○代表false D.◇代表两直线平行,同位角相等
二、填空题
11.平行用符号_____表示,直线AB与CD平行,可以记作为_____.
12.如图,木工师傅可以用角尺画平行线,能解释这一实际应用的数学知识是__________.
13.如图,添加一个你认为合适的条件______使false.
14.如图,直线AB、CD与直线EF相交于E、F,false,当false___时,能使AB//CD.
三、解答题
15.如图,已知b⊥a,c⊥a,试问:b∥c吗?为什么?
16.看图填空,并在括号内说明理由.
(1)∵∠A=∠3(已知)
∴ ∥ .( )
(2)写出两个能得到BC∥DE的条件.
17.如图,补充下列结论和依据.
∵∠ACE=∠D(已知),
∴_____∥______(______________________ ).
∵∠ACE=∠FEC(已知),
∴______∥______(_ ___ _______).
∵∠AEC=∠BOC(已知),
∴_____∥______(___ _____________________).
∵∠BFD+∠FOC=180°(已知),
∴_____∥______(_____ ____________________).
18.填写理由:如图,∠1=∠2,∠3=∠4,false,试说明false.
解:∵∠1=∠2(已知)
∴false(______)
即false=∠______
∵∠3=∠4,false(已知)
∴∠3=∠______(______)
∴∠3=∠______
∴false(______)
19.如图,false,false,证明AD与BC平行.
20.如图,已知false,falsefalsefalse,AE与BF平行吗?为什么?
参考答案
一、选择题
1.C
解:在同一平面内,不重合的两条直线的位置关系是相交或平行,相交包含垂直.
2.B
解:∵a⊥b,a⊥c
∴a∥c.
3.A
解:A选项,
∵∠3=∠5(已知),
∴a∥b(内错角相等,两直线平行).
B选项,∠4=∠7,∠4与∠7无关系,不能判定平行;
C选项,∠2+∠3=180°,∠2与∠3为邻补角,不能判定平行;
D选项,∠1=∠3,∠1与∠3为对顶角,不能判定两直线平行;
4.C
解:A选项,线段AB与线段CD不一定平行,如下图所示,故本选项错误;
B选项,线段AB与线段CD不一定不平行,有可能平行,故本选项错误;
C选项,线段AB与线段CD可能平行,故本选项正确;
D选项,C选项说法正确,故本选项错误.
5.A
在同一平面内,不相交的两条直线必然平行; 在同一平面内,不平行的两条线段延长后必然相交; 在同一平面内,两条直线没有公共点,那么两条直线平行;只有A选项中, 在同一平面内,不相交的两条线段不一定平行,故A错误.
6.D
解:∵∠2和∠4是内错角,
∴根据“内错角相等,两直线平行”可得AD∥BC,
7.C
解:根据题意,第三条直线与这两条平行直线各有一个交点.
8.B
解:①同位角相等,两直线平行,故正确;
②若两个角的和为180°,则这两个角互补,故正确;
③同旁内角互补,两直线平行,故错误;
④内错角相等,两直线平行,故正确.
综上可得①②④正确.
9.B
解:A.∠A=∠BDF,由同位角相等,两直线平行,可判断DF∥AC;
B.∠2=∠4,不能判断DF∥AC;
C.∠1=∠3由内错角相等,两直线平行,可判断DF∥AC;
D.∠A+∠ADF=180°,由同旁内角互补,两直线平行,可判断DF∥AC;
10.D
解:在同一平面内,垂直于同一条直线的两条直线平行,
已知:如图,直线a,b,c,a⊥c,b⊥c.求证:a//b .
解:∵a⊥c(已知),
∴∠1=90°(垂直的定义).
∵b⊥c (已知).
∴∠2=90°(垂直的定义),
∴∠1=∠2 (等量代换),
∴a//b( 同位角相等,两直线平行)
A,△代表 a//b,故A正确,
B,□代表 b⊥c,故B正确,
C,○代表 ∠1=∠2,故C正确,
D,◇代表 同位角相等,两直线平行,故D不正确.
二、填空题
11.∥ AB∥CD
解:平行用符号∥表示,直线AB与CD平行,可以记作为AB∥CD.
12.在同一平面内,垂直于同一条直线的两条直线平行或根据同位角相等两直线平行.
解:如图:∵CD⊥AB,EF⊥AB,
∴CD//EF(在同一平面内,垂直于同一条直线的两条直线平行)
或∵∠ACD=∠AEF=90°,
∴CD//EF(同位角相等两直线平行),
13.∠ADF=∠C或∠A=∠ABE或∠A+∠ABC=180°或∠C+∠ADC=180°(答案不唯一,写一个正确的即可)
第一种情况,同位角相等,两直线平行,即∠ADF=∠C时,false;
第二种情况,内错角相等,两直线平行,即∠A=∠ABE时,false;
第三种情况,同旁内角互补,两直线平行,即∠A+∠ABC=180°或∠C+∠ADC=180°时,false;
14.75°
∵false,
∴false,
要使AB∥CD,则false,
∴false,
三、解答题
15.
解:b∥c,理由如下:
∵b⊥a,c⊥a,
∴∠1=∠2=90°,
∴b∥c(同位角相等,两直线平行).
16.解:
(1)∵∠A=∠3(已知)
∴AC∥BD.(同位角相等,两直线平行)
(2)∠1=∠4;∠2=∠8
因为∠1和∠4是同位角,如果两角相等,那么BC∥DE;
因为∠2和∠8是内错角,如果两角相等,那么BC∥DE.
17.
解:∵∠ACE=∠D(已知),
根据同位角相等两直线平行,
∴CE∥DF.
∵∠ACE=∠FEC,
根据内错角相等,两直线平行,
∴EF∥AD.
∵∠AEC=∠BOC,
根据同位角相等,两直线平行,
∴AE∥BF.
根据∠BFD+∠FOC=180°,
根据同旁内角互补,两直线平行,
∴CE∥DF.
18.解:
∵∠1=∠2(已知)
∴false(等式的性质)
即false=∠ DAC
∵∠3=∠4,false(已知)
∴∠3=∠BAE(等量代换)
∴∠3=∠DAC
∴false(内错角相等,两直线平行)
19.解:
false,且false,
false.
false,
false.
false(同位角相等,两直线平行).
20.解:
false.理由如下:
因为falsefalse,
所以false.
因为false,所以false,
即false.
所以false(同位角相等,两直线平行).
