勾股定理的应用(一)课件
图片预览




文档简介
(共13张PPT)
A
B
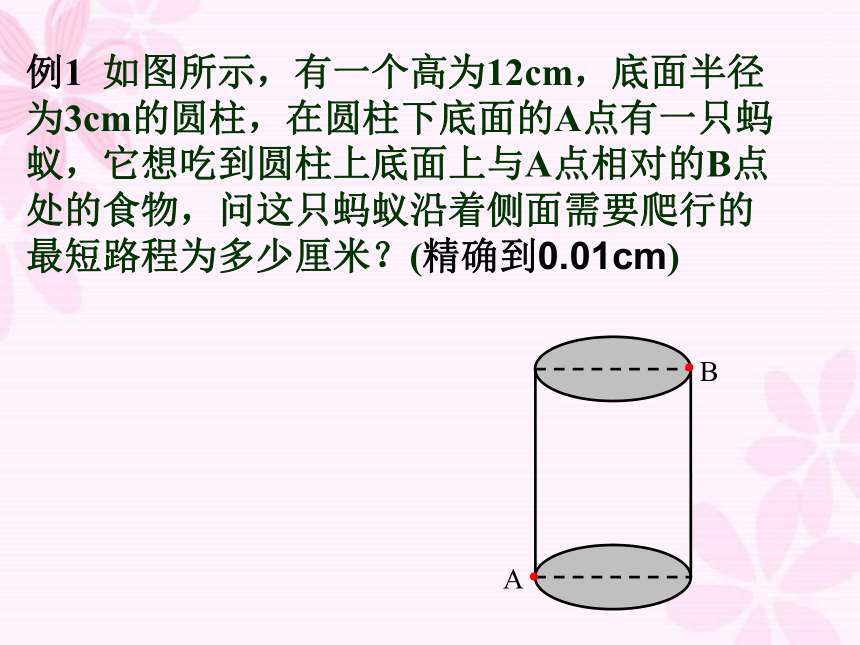
例1 如图所示,有一个高为12cm,底面半径为3cm的圆柱,在圆柱下底面的A点有一只蚂蚁,它想吃到圆柱上底面上与A点相对的B点处的食物,问这只蚂蚁沿着侧面需要爬行的最短路程为多少厘米?(精确到0.01cm)
A
C
B
A
B
例1 如图所示,有一个高为12cm,底面半径为3cm的圆柱,在圆柱下底面的A点有一只蚂蚁,它想吃到圆柱上底面上与A点相对的B点处的食物,问这只蚂蚁沿着侧面需要爬行的最短路程为多少厘米?(精确到0.01cm)
小 结:
把几何体适当展开成平面图形,再利用“两点之间线段最短”性质来解决问题。
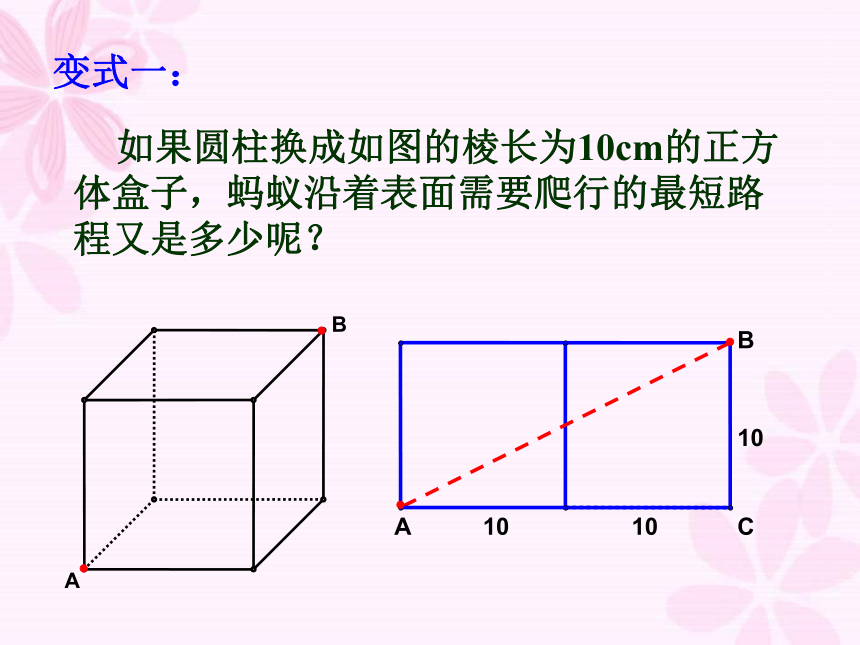
如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面需要爬行的最短路程又是多少呢?
A
B
变式一:
A
B
10
10
10
B
C
A
如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面需要爬行的最短路程又是多少呢?
变式一:
如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面由A爬到C1需要爬行的最短路程又是多少呢?
A
变式二:
B
C
D
B1
C1
D1
A1
分析:蚂蚁由A爬到C1过程中较短的路线有
多少种情况?
(1)经过前面和上底面;
(2)经过前面和右面;
(3)经过左面和上底面.
A
B
C
D
B1
C1
D1
A1
2
3
A
1
B
B1
C1
D1
A1
3
2
1
A
B
C
B1
C1
A1
3
2
1
A
A1
D1
D
B1
C1
(1)当蚂蚁经过前面和上底面时,如图,最短路程为
解:
A
AB=
=
=
B
C
D
B1
C1
D1
A1
2
3
A
1
B
B1
C1
D1
A1
(2)当蚂蚁经过前面和右面时,如图,最短路程为
A
AB=
=
=
B
C
D
B1
C1
D1
A1
3
2
1
A
B
C
B1
C1
A1
(3)当蚂蚁经过左面和上底面时,如图,最短路程为
A
AC1=
=
=
B
C
D
B1
C1
D1
A1
3
2
1
A
A1
D1
D
B1
C1
练习1:如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个
相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
解: ∵ AB2=AC2+BC2=169,
∴ AB=13.
答:从A点爬到B点,最短线路是13.
B
A
D
A
B
C
练习2:如图,长方形中AC=3,CD=5,DF=6,求蚂蚁沿表面从A爬到F的最短距离.
3
5
6
A
C
D
E
B
F
A
B
例1 如图所示,有一个高为12cm,底面半径为3cm的圆柱,在圆柱下底面的A点有一只蚂蚁,它想吃到圆柱上底面上与A点相对的B点处的食物,问这只蚂蚁沿着侧面需要爬行的最短路程为多少厘米?(精确到0.01cm)
A
C
B
A
B
例1 如图所示,有一个高为12cm,底面半径为3cm的圆柱,在圆柱下底面的A点有一只蚂蚁,它想吃到圆柱上底面上与A点相对的B点处的食物,问这只蚂蚁沿着侧面需要爬行的最短路程为多少厘米?(精确到0.01cm)
小 结:
把几何体适当展开成平面图形,再利用“两点之间线段最短”性质来解决问题。
如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面需要爬行的最短路程又是多少呢?
A
B
变式一:
A
B
10
10
10
B
C
A
如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面需要爬行的最短路程又是多少呢?
变式一:
如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面由A爬到C1需要爬行的最短路程又是多少呢?
A
变式二:
B
C
D
B1
C1
D1
A1
分析:蚂蚁由A爬到C1过程中较短的路线有
多少种情况?
(1)经过前面和上底面;
(2)经过前面和右面;
(3)经过左面和上底面.
A
B
C
D
B1
C1
D1
A1
2
3
A
1
B
B1
C1
D1
A1
3
2
1
A
B
C
B1
C1
A1
3
2
1
A
A1
D1
D
B1
C1
(1)当蚂蚁经过前面和上底面时,如图,最短路程为
解:
A
AB=
=
=
B
C
D
B1
C1
D1
A1
2
3
A
1
B
B1
C1
D1
A1
(2)当蚂蚁经过前面和右面时,如图,最短路程为
A
AB=
=
=
B
C
D
B1
C1
D1
A1
3
2
1
A
B
C
B1
C1
A1
(3)当蚂蚁经过左面和上底面时,如图,最短路程为
A
AC1=
=
=
B
C
D
B1
C1
D1
A1
3
2
1
A
A1
D1
D
B1
C1
练习1:如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个
相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
解: ∵ AB2=AC2+BC2=169,
∴ AB=13.
答:从A点爬到B点,最短线路是13.
B
A
D
A
B
C
练习2:如图,长方形中AC=3,CD=5,DF=6,求蚂蚁沿表面从A爬到F的最短距离.
3
5
6
A
C
D
E
B
F
