勾股定理的应用(2)课件
图片预览




文档简介
(共14张PPT)
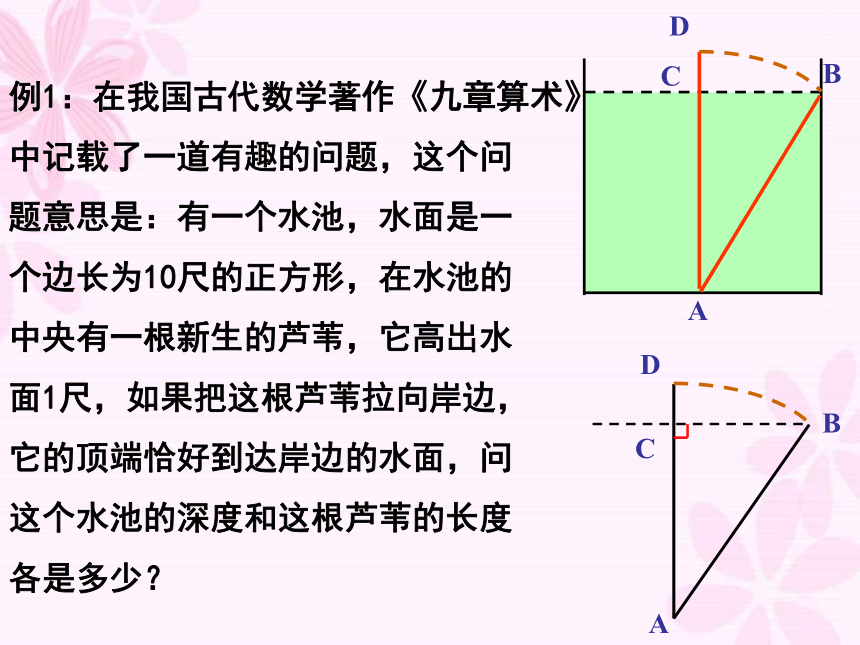
例1:在我国古代数学著作《九章算术》
中记载了一道有趣的问题,这个问
题意思是:有一个水池,水面是一
个边长为10尺的正方形,在水池的
中央有一根新生的芦苇,它高出水
面1尺,如果把这根芦苇拉向岸边,
它的顶端恰好到达岸边的水面,问
这个水池的深度和这根芦苇的长度
各是多少?
D
A
B
C
D
A
B
C
解:设水池的深度为X米,
芦苇高为 (X+1)米.
根据题意得:
在Rt△ABC中,∠ACB=90°
AB2=BC2+AC2
(X+1)2=52+X2
X=12
X+1 =12+1=13(米)
经检验,符合题意
答:水池的深度为12米,芦苇高为13米.
D
A
B
C
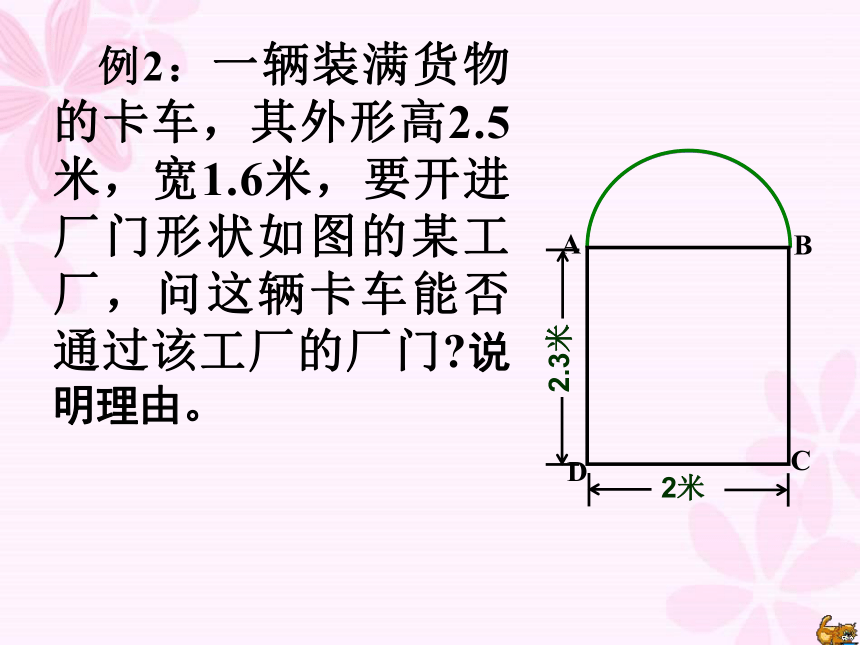
例2:一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门 说明理由。
A
B
C
D
2米
2.3米
A
B
M
N
O
C
┏
D
分析:
H
2米
2.3米
由于厂门宽度足够,所以卡车能否通过,只要看当卡车位于厂门正中间时其高度是否小于CH.如图所示,点D在离厂门中线0.8米处,且CD⊥AB, 与地面交于H.
例2:一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门 说明理由。
解
CD=
CH=0.6+2.3=2.9(米)>2.5(米).
答:卡车能通过厂门.
在Rt△OCD中,∠CDO=90°由勾股定理得
=
=0.6米,
A
B
M
N
O
C
┏
D
H
2米
2.3米
例2:一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门 说明理由。
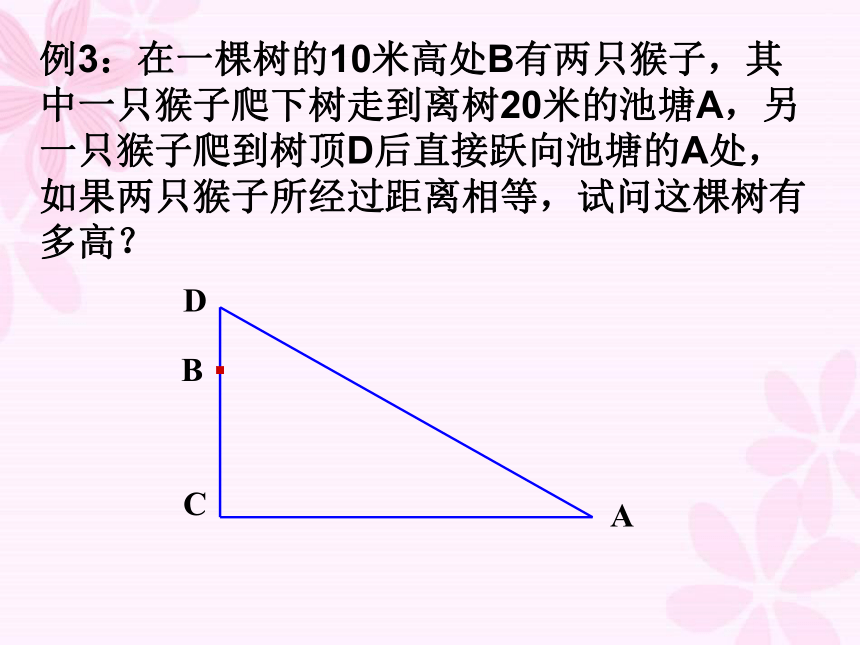
例3:在一棵树的10米高处B有两只猴子,其中一只猴子爬下树走到离树20米的池塘A,另一只猴子爬到树顶D后直接跃向池塘的A处,如果两只猴子所经过距离相等,试问这棵树有多高?
.
D
B
C
A
练习: 两军舰同时从港口O出发执行任务,甲舰以30海里/小时的速度向西北方向航行,乙舰以40海里/小时的速度向西南方向航行,问1小时后两舰相距多远?
甲(A)
西
东
北
南
O
乙(B)
┏
议一议
我们知道数轴上的点有的表示有理数,有的表示无理数,那么 这个数你能用数轴上的点来表示吗?同学们画一画,议一议,小组内交流.
l
作法:
1.在数轴上找点A,使OA=1;
0
1
A
2.作直线l垂直于OA,在l上取点B,使AB=1;
B
C
3.以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示 的点.
归纳结论:
只要能画出长为 的线段,就能在数轴上画出表示这个数的点.
是两条直角边都是1的直角三角形的斜边.
思考与探究
怎样作出长为 , , , ,
……的线段呢?请你画出来,并说说理由.
利用勾股定理,构造直角三角形,我们就可以得到长为 , , ……的线段,如下图.
从而在数轴上画出表示 , , ……的点.
1
1
1
1
1
1
1
1
1
1
1
1
1
长为 的线段是直角边为正整数______,______的直角三角形的斜边.
长为 的线段是直角边为正整数______,______的直角三角形的斜边.
并在数轴上画出表示 , 的点.
思考与探究
2
1
2
3
例1:在我国古代数学著作《九章算术》
中记载了一道有趣的问题,这个问
题意思是:有一个水池,水面是一
个边长为10尺的正方形,在水池的
中央有一根新生的芦苇,它高出水
面1尺,如果把这根芦苇拉向岸边,
它的顶端恰好到达岸边的水面,问
这个水池的深度和这根芦苇的长度
各是多少?
D
A
B
C
D
A
B
C
解:设水池的深度为X米,
芦苇高为 (X+1)米.
根据题意得:
在Rt△ABC中,∠ACB=90°
AB2=BC2+AC2
(X+1)2=52+X2
X=12
X+1 =12+1=13(米)
经检验,符合题意
答:水池的深度为12米,芦苇高为13米.
D
A
B
C
例2:一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门 说明理由。
A
B
C
D
2米
2.3米
A
B
M
N
O
C
┏
D
分析:
H
2米
2.3米
由于厂门宽度足够,所以卡车能否通过,只要看当卡车位于厂门正中间时其高度是否小于CH.如图所示,点D在离厂门中线0.8米处,且CD⊥AB, 与地面交于H.
例2:一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门 说明理由。
解
CD=
CH=0.6+2.3=2.9(米)>2.5(米).
答:卡车能通过厂门.
在Rt△OCD中,∠CDO=90°由勾股定理得
=
=0.6米,
A
B
M
N
O
C
┏
D
H
2米
2.3米
例2:一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门 说明理由。
例3:在一棵树的10米高处B有两只猴子,其中一只猴子爬下树走到离树20米的池塘A,另一只猴子爬到树顶D后直接跃向池塘的A处,如果两只猴子所经过距离相等,试问这棵树有多高?
.
D
B
C
A
练习: 两军舰同时从港口O出发执行任务,甲舰以30海里/小时的速度向西北方向航行,乙舰以40海里/小时的速度向西南方向航行,问1小时后两舰相距多远?
甲(A)
西
东
北
南
O
乙(B)
┏
议一议
我们知道数轴上的点有的表示有理数,有的表示无理数,那么 这个数你能用数轴上的点来表示吗?同学们画一画,议一议,小组内交流.
l
作法:
1.在数轴上找点A,使OA=1;
0
1
A
2.作直线l垂直于OA,在l上取点B,使AB=1;
B
C
3.以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示 的点.
归纳结论:
只要能画出长为 的线段,就能在数轴上画出表示这个数的点.
是两条直角边都是1的直角三角形的斜边.
思考与探究
怎样作出长为 , , , ,
……的线段呢?请你画出来,并说说理由.
利用勾股定理,构造直角三角形,我们就可以得到长为 , , ……的线段,如下图.
从而在数轴上画出表示 , , ……的点.
1
1
1
1
1
1
1
1
1
1
1
1
1
长为 的线段是直角边为正整数______,______的直角三角形的斜边.
长为 的线段是直角边为正整数______,______的直角三角形的斜边.
并在数轴上画出表示 , 的点.
思考与探究
2
1
2
3
