四川省江油市八校联考2020-2021学年第二学期九年级数学开学考试试题(word版,含答案)
文档属性
| 名称 | 四川省江油市八校联考2020-2021学年第二学期九年级数学开学考试试题(word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 248.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 17:25:31 | ||
图片预览



文档简介
2021年春四川省江油市八校联考(入学测试)人教版数学九年级试卷
班级 姓名
一.选择题
1.如果二次根式 x+3 在实数范围内有意义,那么x的取值范围是( )
A.x≠﹣3 B.x≤﹣3
C.x≥﹣3 D.x>﹣3
2.下列各式是最简二次根式的是( )
A. 13 B.12
C. a2 D.53
3.若 a 化成最简二次根式后,能与2合并,则a的值不可以是( )
A.12 B.8 C.18 D.28
4.x=1是关于x的一元二次方程x2+ax+2b=0的解,则a+2b=( )
A.﹣1 B.1 C .2 D.﹣2
5.已知实数x满足(x2﹣2x+1)2+4 (x2﹣2x+1)﹣5=0,那么x2﹣2x+1的值为( )
A.﹣5或1 B.﹣1或5 C.1 D.5
6.在平面直角坐标系中,点(3,﹣5)关于原点对称的点是( )
A.(3,﹣5) B.(﹣3,5) C.(5,﹣3) D.(﹣3,﹣5)
7.直径为10分米的圆柱形排水管,截面如图所示.若管内有积水(阴影部分),水面宽AB为8分米,则积水的最大深度CD为( )
A.2分米 B.3分米 C.4分米 D.5分米
8.如图,点A、B、C分别表示三个村庄,AB=13千米,BC=5千米,AC=12千米.某社区拟建一个文化活动中心.要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
A.AB中点 B.BC中点
C.AC中点 D . ∠C的平分线与AB的交点
9.若一个圆内接正多边形的内角是108°,则这个多边形是( )
A.正五边形 B.正六边形
C.正八边形 D.正十边形
10.若一个扇形的圆心角为90°,半径为6,则该扇形的面积为( )
A. 3π2 B.3π C.6π D.9π
11.下列事件中,属于随机事件的是( )
A.用长度分别是4cm,4cm,9cm的细木条首尾顺次相连可组成一个等腰三角形
B.以长度分别是5cm,4cm,3cm的线段为三角形三边,能构成直角三角形
C.分式的分子、分母同乘一个不等于零的整式,分式的值不变
D.任意画一个三角形,恰好是同一条边上的高线与中线重合
12.抛物线y=x2+x﹣6与y轴的交点坐标是( )
A.(0,6) B.(0,﹣6)
C.(﹣6,0) D.(﹣3,0),(2,0)
13.已知抛物线y=ax2+bx+c的对称轴为直线x=3,与x轴的一个交点坐标为(0,0),其部分图象如图所示,下列结论正确的是( )
A.a﹣b+c<0
B.6a﹣b=0
C.抛物线过(6,0)
D.当x<3时,y随x增大而增大
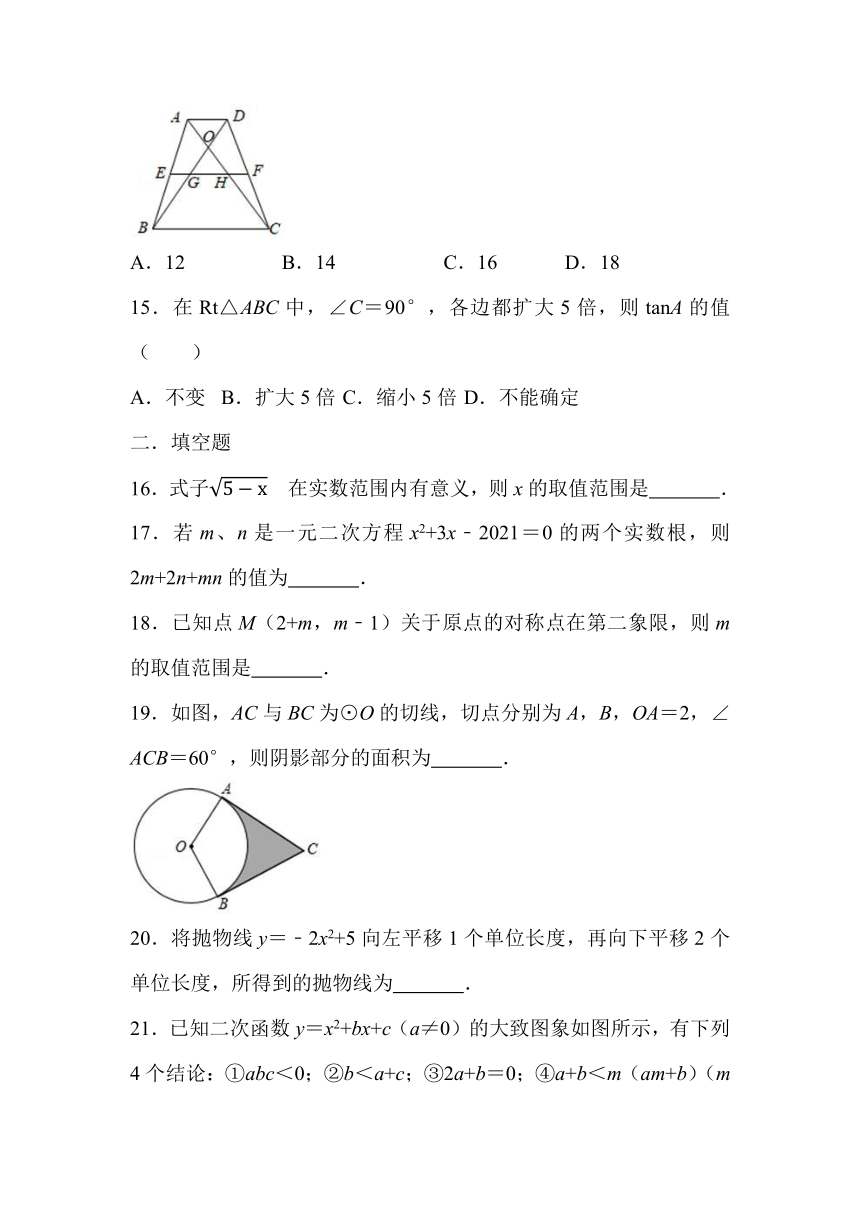
14.如图,在梯形ABCD中,AD∥BC,BC=3AD,对角线AC、BD交于点O,EF是梯形ABCD的中位线,EF与BD、AC分别交于点G、H,如果△OGH的面积为1,那么梯形ABCD的面积为( )
A.12 B.14 C.16 D.18
15.在Rt△ABC中,∠C=90°,各边都扩大5倍,则tanA的值( )
A.不变 B.扩大5倍 C.缩小5倍 D.不能确定
二.填空题
16.式子5-x 在实数范围内有意义,则x的取值范围是 .
17.若m、n是一元二次方程x2+3x﹣2021=0的两个实数根,则2m+2n+mn的值为 .
18.已知点M(2+m,m﹣1)关于原点的对称点在第二象限,则m的取值范围是 .
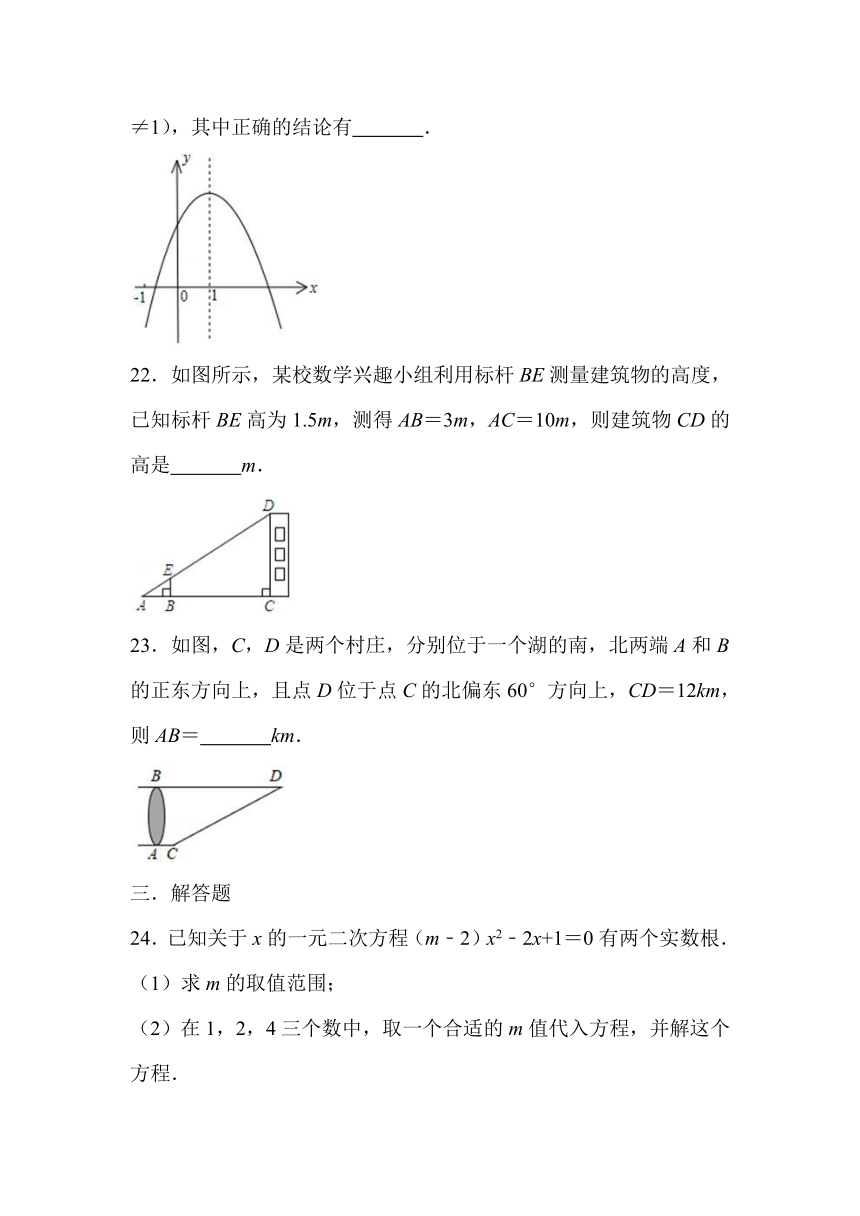
19.如图,AC与BC为⊙O的切线,切点分别为A,B,OA=2,∠ACB=60°,则阴影部分的面积为 .
20.将抛物线y=﹣2x2+5向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为 .
21.已知二次函数y=x2+bx+c(a≠0)的大致图象如图所示,有下列4个结论:①abc<0;②b<a+c;③2a+b=0;④a+b<m(am+b)(m≠1),其中正确的结论有 .
22.如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高为1.5m,测得AB=3m,AC=10m,则建筑物CD的高是 m.
23.如图,C,D是两个村庄,分别位于一个湖的南,北两端A和B的正东方向上,且点D位于点C的北偏东60°方向上,CD=12km,则AB= km.
三.解答题
24.已知关于x的一元二次方程(m﹣2)x2﹣2x+1=0有两个实数根.
(1)求m的取值范围;
(2)在1,2,4三个数中,取一个合适的m值代入方程,并解这个方程.
25.(1)计算:(﹣2)2﹣|﹣3|+2× 8+(﹣6)0;
(2)解分式方程:2x-1= 5 x2-1.
26.如图,已知四边形ABCD,∠B=∠D=60°,AD为直径的⊙O经过点C,AB是⊙O的切线,OE∥BC.
(1)求证:BC是⊙O的切线;
(2)若AE=1,求BE的长.
27.2020年春季在新冠疫情的背景下,全国各大中小学纷纷开设空中课堂,学生要面对电脑等电子产品上网课,某校为了解本校学生对自己视力保护的重视程度,随机在校内调查了部分学生,调直结果分为“非常重视”“重视”“比较重视”“不重视”四类,并将结果绘制成如图所示的两幅不完整的统计图:根据图中信息,解答下列问题:
(1)在扇形统计图中,“比较重视”所占的圆心角的度数为 ,并补全条形统计图;
(2)该校共有学生3200人,请你估计该校对视力保护“非常重视”的学生人数;
(3)对视力“非常重视”的4人有A1,A2两名男生,B1,B2两名女生,若从中随机抽取两人向全校作视力保护经验交流,请利用树状图或列表法,求出恰好抽到同性别学生的概率.
28.如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:PB是⊙O的切线;
(2)OP与⊙O相交于点D,直线CD交PB于点E,若CE⊥PB,CE=4,求⊙O的半径.
29.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣4与x轴交于点A(﹣4,0)和点B(2,0),与y轴交于点C.
(1)求该抛物线的表达式及点C的坐标;
(2)如果点D的坐标为(﹣8,0),联结AC、DC,求∠ACD的正切值;
(3)在(2)的条件下,点P为抛物线上一点,当∠OCD=∠CAP时,求点P的坐标.
参考答案
一.选择题
1.C; 2.A; 3.D; 4.A; 5.C; 6.B; 7.A; 8.A; 9.A; 10.D; 11.D; 12.B; 13.C; 14.C; 15.A;
二.填空题
16.x≤5; 17.﹣2027; 18.﹣2<m<1; 19.43 ﹣43π; 20.y=﹣2(x+1)2+3; 21.①③; 22.5; 23.6;
三.解答题(共6小题)
24.
解: (1 )根据题意,b2-4ac=(-2 ) 2-4 (m-2 )≥0,且m-2≠0
.m≤3,m≠2 ;
(2 ) ∵:m≤3且m≠2
∴可取m=1 ,
当m=1时,原方程化为-x2-2x+1=0 ,
25
解:(1)原式=4-3+4+1=6 ;
(2 )两边都乘以( x+1) (x-1) ,得:2(x+1 )=5
解得:x=32
检验:当x= 32 时,(x+1 ) (x-1 )= 54 ≠0.
.原分式方程的解为x= 32
26.
解:(1)连接OC,
图1
∵∠B=∠D=60° ,
∴OODC为等边三角形,
∴∠DC0=60°,
∵A B是00的切线,
∴∠OAB=90° ,
∵∠A+∠B+∠C+∠BCD=360° ,
∴∠BOC=360°-∠A-∠B-∠D-∠0CD=360°-90°- 60°- 60°-60°=90°
∴0C⊥BC,
∴BC是00的切线;
(2)如图,连接OB,
图2
∵OE//BC ,∠ABC=60° ,
∴∠OEA=∠ABC=60° ,
∴∠AOE=90°-∠OEA=30° ,
∵AE=1
∴OE=2AE=2 ,
27.162°;
28.
(1)证明:连接OC,过点O作OT⊥PB于T
∵PA是00的切线,
∵0C⊥PA,
∵OP平分∠APB,OT⊥PB .
∴0C=OT ,
∴PB是00的切线.
( 2)∵CE⊥PB , OT⊥PB
∴∠CEP=∠OTP=90°
∴CE//OT,
∴∠ODC=∠DOT ,
∵PA , PB是00的切线,
∴PC=PT ,
在OOPC和OOPT中,
pc=pTPO=POOC=OT
∴OOPC≌OOPT ( SSS ),
∴∠POC=∠POD=∠ODC ,
∵0C=0D
∴∠ODC=∠OCD,
∴∠COD=∠0CD=∠ODC=60°
∴OOCD是等边三角形,
∴CD=0C=OD ,
∴∠OPC=90°-60°=30°
∵∠ODC=∠DCP+∠DPC ,
∴∠DCP=∠DPC=30°,
∴DC=DP=OD ,
∵DE//OT ,
∴ET=EP,
29.
(2 )如图1 ,过D作DE⊥AC交CA延长线于E ,
班级 姓名
一.选择题
1.如果二次根式 x+3 在实数范围内有意义,那么x的取值范围是( )
A.x≠﹣3 B.x≤﹣3
C.x≥﹣3 D.x>﹣3
2.下列各式是最简二次根式的是( )
A. 13 B.12
C. a2 D.53
3.若 a 化成最简二次根式后,能与2合并,则a的值不可以是( )
A.12 B.8 C.18 D.28
4.x=1是关于x的一元二次方程x2+ax+2b=0的解,则a+2b=( )
A.﹣1 B.1 C .2 D.﹣2
5.已知实数x满足(x2﹣2x+1)2+4 (x2﹣2x+1)﹣5=0,那么x2﹣2x+1的值为( )
A.﹣5或1 B.﹣1或5 C.1 D.5
6.在平面直角坐标系中,点(3,﹣5)关于原点对称的点是( )
A.(3,﹣5) B.(﹣3,5) C.(5,﹣3) D.(﹣3,﹣5)
7.直径为10分米的圆柱形排水管,截面如图所示.若管内有积水(阴影部分),水面宽AB为8分米,则积水的最大深度CD为( )
A.2分米 B.3分米 C.4分米 D.5分米
8.如图,点A、B、C分别表示三个村庄,AB=13千米,BC=5千米,AC=12千米.某社区拟建一个文化活动中心.要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
A.AB中点 B.BC中点
C.AC中点 D . ∠C的平分线与AB的交点
9.若一个圆内接正多边形的内角是108°,则这个多边形是( )
A.正五边形 B.正六边形
C.正八边形 D.正十边形
10.若一个扇形的圆心角为90°,半径为6,则该扇形的面积为( )
A. 3π2 B.3π C.6π D.9π
11.下列事件中,属于随机事件的是( )
A.用长度分别是4cm,4cm,9cm的细木条首尾顺次相连可组成一个等腰三角形
B.以长度分别是5cm,4cm,3cm的线段为三角形三边,能构成直角三角形
C.分式的分子、分母同乘一个不等于零的整式,分式的值不变
D.任意画一个三角形,恰好是同一条边上的高线与中线重合
12.抛物线y=x2+x﹣6与y轴的交点坐标是( )
A.(0,6) B.(0,﹣6)
C.(﹣6,0) D.(﹣3,0),(2,0)
13.已知抛物线y=ax2+bx+c的对称轴为直线x=3,与x轴的一个交点坐标为(0,0),其部分图象如图所示,下列结论正确的是( )
A.a﹣b+c<0
B.6a﹣b=0
C.抛物线过(6,0)
D.当x<3时,y随x增大而增大
14.如图,在梯形ABCD中,AD∥BC,BC=3AD,对角线AC、BD交于点O,EF是梯形ABCD的中位线,EF与BD、AC分别交于点G、H,如果△OGH的面积为1,那么梯形ABCD的面积为( )
A.12 B.14 C.16 D.18
15.在Rt△ABC中,∠C=90°,各边都扩大5倍,则tanA的值( )
A.不变 B.扩大5倍 C.缩小5倍 D.不能确定
二.填空题
16.式子5-x 在实数范围内有意义,则x的取值范围是 .
17.若m、n是一元二次方程x2+3x﹣2021=0的两个实数根,则2m+2n+mn的值为 .
18.已知点M(2+m,m﹣1)关于原点的对称点在第二象限,则m的取值范围是 .
19.如图,AC与BC为⊙O的切线,切点分别为A,B,OA=2,∠ACB=60°,则阴影部分的面积为 .
20.将抛物线y=﹣2x2+5向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为 .
21.已知二次函数y=x2+bx+c(a≠0)的大致图象如图所示,有下列4个结论:①abc<0;②b<a+c;③2a+b=0;④a+b<m(am+b)(m≠1),其中正确的结论有 .
22.如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高为1.5m,测得AB=3m,AC=10m,则建筑物CD的高是 m.
23.如图,C,D是两个村庄,分别位于一个湖的南,北两端A和B的正东方向上,且点D位于点C的北偏东60°方向上,CD=12km,则AB= km.
三.解答题
24.已知关于x的一元二次方程(m﹣2)x2﹣2x+1=0有两个实数根.
(1)求m的取值范围;
(2)在1,2,4三个数中,取一个合适的m值代入方程,并解这个方程.
25.(1)计算:(﹣2)2﹣|﹣3|+2× 8+(﹣6)0;
(2)解分式方程:2x-1= 5 x2-1.
26.如图,已知四边形ABCD,∠B=∠D=60°,AD为直径的⊙O经过点C,AB是⊙O的切线,OE∥BC.
(1)求证:BC是⊙O的切线;
(2)若AE=1,求BE的长.
27.2020年春季在新冠疫情的背景下,全国各大中小学纷纷开设空中课堂,学生要面对电脑等电子产品上网课,某校为了解本校学生对自己视力保护的重视程度,随机在校内调查了部分学生,调直结果分为“非常重视”“重视”“比较重视”“不重视”四类,并将结果绘制成如图所示的两幅不完整的统计图:根据图中信息,解答下列问题:
(1)在扇形统计图中,“比较重视”所占的圆心角的度数为 ,并补全条形统计图;
(2)该校共有学生3200人,请你估计该校对视力保护“非常重视”的学生人数;
(3)对视力“非常重视”的4人有A1,A2两名男生,B1,B2两名女生,若从中随机抽取两人向全校作视力保护经验交流,请利用树状图或列表法,求出恰好抽到同性别学生的概率.
28.如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:PB是⊙O的切线;
(2)OP与⊙O相交于点D,直线CD交PB于点E,若CE⊥PB,CE=4,求⊙O的半径.
29.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣4与x轴交于点A(﹣4,0)和点B(2,0),与y轴交于点C.
(1)求该抛物线的表达式及点C的坐标;
(2)如果点D的坐标为(﹣8,0),联结AC、DC,求∠ACD的正切值;
(3)在(2)的条件下,点P为抛物线上一点,当∠OCD=∠CAP时,求点P的坐标.
参考答案
一.选择题
1.C; 2.A; 3.D; 4.A; 5.C; 6.B; 7.A; 8.A; 9.A; 10.D; 11.D; 12.B; 13.C; 14.C; 15.A;
二.填空题
16.x≤5; 17.﹣2027; 18.﹣2<m<1; 19.43 ﹣43π; 20.y=﹣2(x+1)2+3; 21.①③; 22.5; 23.6;
三.解答题(共6小题)
24.
解: (1 )根据题意,b2-4ac=(-2 ) 2-4 (m-2 )≥0,且m-2≠0
.m≤3,m≠2 ;
(2 ) ∵:m≤3且m≠2
∴可取m=1 ,
当m=1时,原方程化为-x2-2x+1=0 ,
25
解:(1)原式=4-3+4+1=6 ;
(2 )两边都乘以( x+1) (x-1) ,得:2(x+1 )=5
解得:x=32
检验:当x= 32 时,(x+1 ) (x-1 )= 54 ≠0.
.原分式方程的解为x= 32
26.
解:(1)连接OC,
图1
∵∠B=∠D=60° ,
∴OODC为等边三角形,
∴∠DC0=60°,
∵A B是00的切线,
∴∠OAB=90° ,
∵∠A+∠B+∠C+∠BCD=360° ,
∴∠BOC=360°-∠A-∠B-∠D-∠0CD=360°-90°- 60°- 60°-60°=90°
∴0C⊥BC,
∴BC是00的切线;
(2)如图,连接OB,
图2
∵OE//BC ,∠ABC=60° ,
∴∠OEA=∠ABC=60° ,
∴∠AOE=90°-∠OEA=30° ,
∵AE=1
∴OE=2AE=2 ,
27.162°;
28.
(1)证明:连接OC,过点O作OT⊥PB于T
∵PA是00的切线,
∵0C⊥PA,
∵OP平分∠APB,OT⊥PB .
∴0C=OT ,
∴PB是00的切线.
( 2)∵CE⊥PB , OT⊥PB
∴∠CEP=∠OTP=90°
∴CE//OT,
∴∠ODC=∠DOT ,
∵PA , PB是00的切线,
∴PC=PT ,
在OOPC和OOPT中,
pc=pTPO=POOC=OT
∴OOPC≌OOPT ( SSS ),
∴∠POC=∠POD=∠ODC ,
∵0C=0D
∴∠ODC=∠OCD,
∴∠COD=∠0CD=∠ODC=60°
∴OOCD是等边三角形,
∴CD=0C=OD ,
∴∠OPC=90°-60°=30°
∵∠ODC=∠DCP+∠DPC ,
∴∠DCP=∠DPC=30°,
∴DC=DP=OD ,
∵DE//OT ,
∴ET=EP,
29.
(2 )如图1 ,过D作DE⊥AC交CA延长线于E ,
同课章节目录
