四川省江油市八校联考2020-2021学年第二学期七年级数学开学考试试题(word版,含答案)
文档属性
| 名称 | 四川省江油市八校联考2020-2021学年第二学期七年级数学开学考试试题(word版,含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 143.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 00:00:00 | ||
图片预览




文档简介
2021年春四川省江油市八校联考(入学测试)人教版数学七年级试卷
班级 姓名
一.选择题
1.冰箱冷藏室的温度零上6℃,记作+6℃,冷冻室的温度零下18℃,记作( )
A.18℃ B.12℃ C.﹣18℃ D.﹣24℃
2.一小袋味精的质量标准为“50±0.25克 ”,那么下列四小袋味精质量符合要求的是( )
A.50.35克 B.49.80克 C.49.72克 D.50.40克
3.在﹣13 ,227 ,0,﹣1,0.4,π,2,﹣3,﹣6这些数中,有理数有m个,自然数有n个,分数有k个,则m﹣n﹣k的值为( )
A.3 B.2 C.1 D.4
4.有理数a在数轴上的对应点的位置如图所示,若有理数b满足﹣a<b<a,则b的值不可能是( )
A.2 B.0 C.﹣1 D.﹣3
5.已知a是一个正整数,记G(x)=a﹣x+|x﹣a|.若G(1)+G(2)+G(3)+…+G(2019)+G(2020)=90,则a的值为( )
A.11 B.10 C.9 D.8
6.下列运算正确的是( )
A.﹣2+(﹣5)=﹣(5﹣2)=﹣3
B.(+3)+(﹣8)=﹣(8﹣3)=﹣5
C.(﹣9)﹣(﹣2)=﹣(9+2)=﹣11
D.(+6)+(﹣4)=+(6+4)=+10
7.有理数a、b在数轴上的位置如图所示,则下列各式:①a+b>0;②a﹣b>0;③|b|>a;④ab<0;⑤|b﹣a|=a﹣b,正确的有( )
A.1个 B.2个 C.3个 D.4个
8.用四舍五入法按要求把2.0503分别取近似数,其中错误的是( )
A.2.1(精确到0.1) B.2.05(精确到0.001)
C.2.05(精确到百分位) D.2.050(精确到千分位)
9.若x2﹣3x=4,则3x2﹣9x+8的值是( )
A.20 B.16 C.4 D.﹣4
10.下列合并同类项正确的是( )
A.15a﹣15a=15 B.3a2﹣a2=2
C.3x+5y=8xy D.7x2﹣6x2=x2
11.如图,点D是线段AB的中点,点C是线段AD的中点.若AB=16cm,则线段BC=( )
A.4cm B.10cm C.12cm D.14cm
12.如图∠AOB=60°,射线OC平分∠AOB,以OC为一边作∠COP=15°,则∠BOP=( )
A.15° B.45° C.15°或30° D.15°或45°
二.填空题(共7小题)
13.﹣8的相反数是 .如果﹣a=2,则a= .
14.如图,数轴上M点表示的数为m,化简|3+m|+2|2+m|﹣|m﹣3|= .
15.若x、y都是整数,且(2y+3)2+|x﹣1|=1,则x﹣y= .
16.若代数式﹣(3x3ym﹣1)+3(xny+1)经过化简后的结果等于4,则m﹣n的值是 .
17.已知2x+1与x+5互为相反数,则x= .
18.甲,乙二人分别从一条笔直的公路上的AB两地同时出发相向而行,甲每分钟走60米,乙每分钟走48米,5分钟后两人相距20米,则A.B两地之间的距离为 米.
19.如图,点C是线段AB上一点,点M、N、P分别是线段AC,BC,AB的中点.AC=3cm,CP=1cm,线段PN= cm.
三.解答题(共7小题)
20.一名足球守门员练习折返跑,从球门线出发,向前记为正数,返回记为负数,他的记录如下(单位:米):+5,﹣3,+10,﹣8,﹣6,+12,﹣10,
(1)守门员最后是否回到了球门线的位置?
(2)守门员全部练习结束后,共跑了多少米?
(3)在练习过程中,守门员离开球门线的最远距离是多少米?
21.计算:
(1)2﹣(﹣4)+8÷(﹣2)+(﹣3)
(2)﹣36×(23 + 34 - 112 )
(3)﹣23÷8﹣14 ×(﹣2)2.
22.已知A=3x2﹣x+2y﹣4xy,B=2x2﹣3x﹣y+xy.
(1)化简2A﹣3B;
(2)当x+y=67 ,xy=﹣1,求2A﹣3B的值;
(3)若2A﹣3B的值与y的取值无关,求2A﹣3B的值.
23.数学中,运用整体思想方法在求代数式的值时非常重要.
例如:已知a2+2a=2,则代数式2a2+4a+3=2(a2+2a)+3=2×2+3=7.
请你根据以上材料解答以下问题:
(1)若x2﹣3x=4,求1﹣x2+3x的值.
(2)当x=1时,代数式px3+qx﹣1的值是5,求当x=﹣1时,代数式px3+qx﹣1的值.
(3)当x=2020时,代数式ax5+bx3+cx+6的值为m,直接写出当x=﹣2020时,代数式ax5+bx3+cx+6的值.(用含m的代数式表示)
24.解下列一元一次方程:
(1)2x﹣(x+10)=5x+2(x﹣1);
(2)=.
25.某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个.2个甲种部件和3个乙种部件配成一套,问加工甲乙部件各安排多少人才能使每天加工的甲、乙两种部件刚好配套?
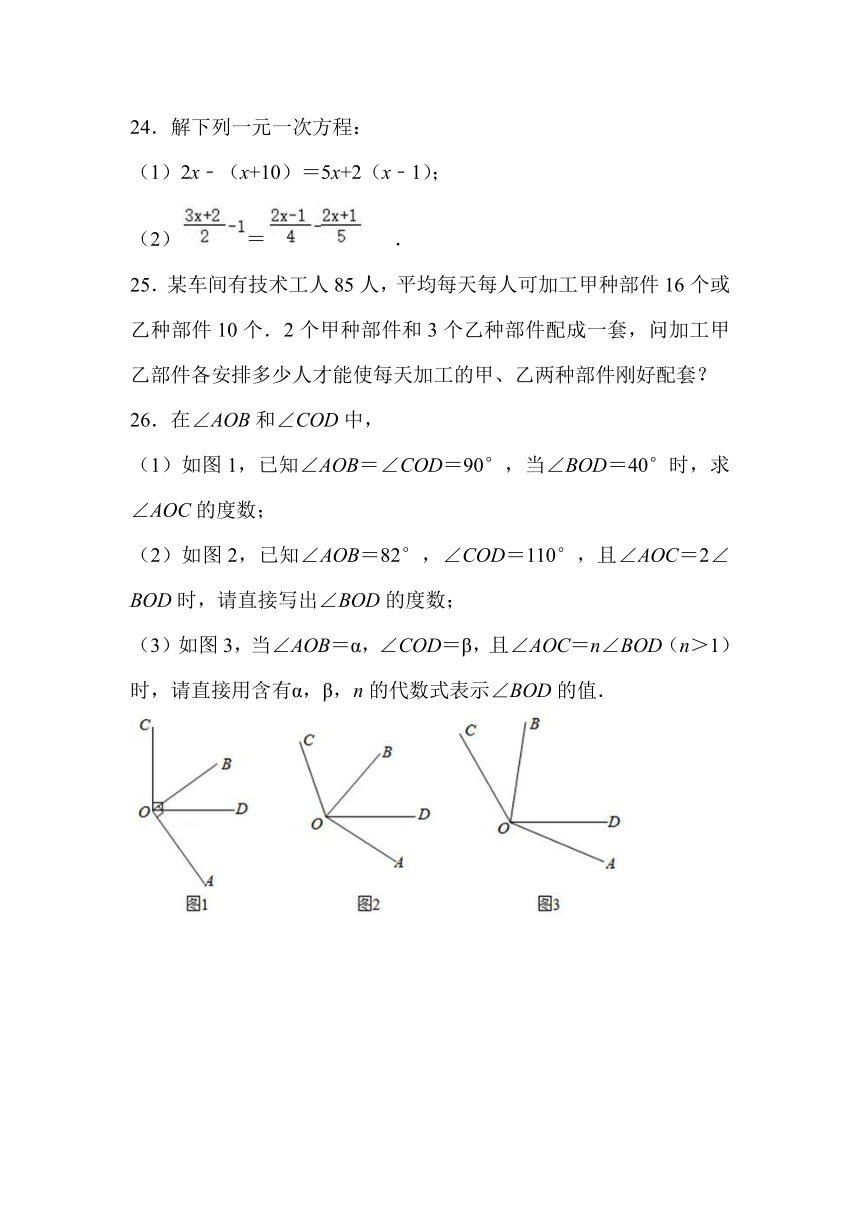
26.在∠AOB和∠COD中,
(1)如图1,已知∠AOB=∠COD=90°,当∠BOD=40°时,求∠AOC的度数;
(2)如图2,已知∠AOB=82°,∠COD=110°,且∠AOC=2∠BOD时,请直接写出∠BOD的度数;
(3)如图3,当∠AOB=α,∠COD=β,且∠AOC=n∠BOD(n>1)时,请直接用含有α,β,n的代数式表示∠BOD的值.
参考答案
一.选择题
1.C; 2.B; 3.A; 4.D; 5.B;
6.B; 7.D; 8.B; 9.A; 10.D;
11.C; 12.D;
二.填空题
13.8;﹣2;
14.﹣4;
15.2或3;
16.﹣2;
17.﹣2;
18.520或560;
19 . 32;
三.解答题
20.解:(1)(+5)+(-3)+(+10)+ (-8) +(-6)+ (+12) + (-10)
= ( 5+10+12 )- ( 3+8+6+10 )
二27- 27
=0 ,
答:守门员最后回到了球门线的位置;
(2) |+5|+-31+1+ 10|+|- 81+1-61+1+12|+1-10|
=5+3+10+8+6+12+ 10
=54 ;
答:守门员全部练习结束后,他共跑了54米;
(3 )由观察可知:在练习过程中,守门员离开球[门线最远距离是12米.
21.解:(1)原式=2+4-4-3=-1 ;
( 2 )原式=-24-27+3=-48 ;
( 3 )原式=-1-1=-2.
22.
解:(1)::A=3x2-x+2y-4xy,B=2x2-3x-y+xy ,
. ..2A-3B
=2 ( 3x2-x+2y-4xy ) -3 ( 2x2-3x-y+xy )
=6x2- 2x +4y- 8xy- 6x2+9x+3y-3xy
=7x+7y-11xy ;
(3) :24A-3B=7x+7y-11xy
=7x+ (7-11x)y,
.:若2A-3B的值与y的取值无关,则7-11x=0 ,
23.
24.
解:(1 )去括号得:2x-x-10=5x+2x-2,
移项得: 2x-x-5x-2x=-2+10 ,
合并得: -6x=8 ,
(2)去分母得:10(3x+2)-20=5(2x-1)-4(2x+1)。
去括号得: 30x+20-20= 10x-5-8x-4,
移项合并得: 28x=-9 ,
25.
解:设安排x人加工甲部件,则安排( 85-x )人加工乙部件,根据题意得
3x16x=2x10x(85-x) ,
解得x=25,
所以85-25=60 (人) ,
答:安排25人加工甲部件, 安排60人加工乙部件.
26.
班级 姓名
一.选择题
1.冰箱冷藏室的温度零上6℃,记作+6℃,冷冻室的温度零下18℃,记作( )
A.18℃ B.12℃ C.﹣18℃ D.﹣24℃
2.一小袋味精的质量标准为“50±0.25克 ”,那么下列四小袋味精质量符合要求的是( )
A.50.35克 B.49.80克 C.49.72克 D.50.40克
3.在﹣13 ,227 ,0,﹣1,0.4,π,2,﹣3,﹣6这些数中,有理数有m个,自然数有n个,分数有k个,则m﹣n﹣k的值为( )
A.3 B.2 C.1 D.4
4.有理数a在数轴上的对应点的位置如图所示,若有理数b满足﹣a<b<a,则b的值不可能是( )
A.2 B.0 C.﹣1 D.﹣3
5.已知a是一个正整数,记G(x)=a﹣x+|x﹣a|.若G(1)+G(2)+G(3)+…+G(2019)+G(2020)=90,则a的值为( )
A.11 B.10 C.9 D.8
6.下列运算正确的是( )
A.﹣2+(﹣5)=﹣(5﹣2)=﹣3
B.(+3)+(﹣8)=﹣(8﹣3)=﹣5
C.(﹣9)﹣(﹣2)=﹣(9+2)=﹣11
D.(+6)+(﹣4)=+(6+4)=+10
7.有理数a、b在数轴上的位置如图所示,则下列各式:①a+b>0;②a﹣b>0;③|b|>a;④ab<0;⑤|b﹣a|=a﹣b,正确的有( )
A.1个 B.2个 C.3个 D.4个
8.用四舍五入法按要求把2.0503分别取近似数,其中错误的是( )
A.2.1(精确到0.1) B.2.05(精确到0.001)
C.2.05(精确到百分位) D.2.050(精确到千分位)
9.若x2﹣3x=4,则3x2﹣9x+8的值是( )
A.20 B.16 C.4 D.﹣4
10.下列合并同类项正确的是( )
A.15a﹣15a=15 B.3a2﹣a2=2
C.3x+5y=8xy D.7x2﹣6x2=x2
11.如图,点D是线段AB的中点,点C是线段AD的中点.若AB=16cm,则线段BC=( )
A.4cm B.10cm C.12cm D.14cm
12.如图∠AOB=60°,射线OC平分∠AOB,以OC为一边作∠COP=15°,则∠BOP=( )
A.15° B.45° C.15°或30° D.15°或45°
二.填空题(共7小题)
13.﹣8的相反数是 .如果﹣a=2,则a= .
14.如图,数轴上M点表示的数为m,化简|3+m|+2|2+m|﹣|m﹣3|= .
15.若x、y都是整数,且(2y+3)2+|x﹣1|=1,则x﹣y= .
16.若代数式﹣(3x3ym﹣1)+3(xny+1)经过化简后的结果等于4,则m﹣n的值是 .
17.已知2x+1与x+5互为相反数,则x= .
18.甲,乙二人分别从一条笔直的公路上的AB两地同时出发相向而行,甲每分钟走60米,乙每分钟走48米,5分钟后两人相距20米,则A.B两地之间的距离为 米.
19.如图,点C是线段AB上一点,点M、N、P分别是线段AC,BC,AB的中点.AC=3cm,CP=1cm,线段PN= cm.
三.解答题(共7小题)
20.一名足球守门员练习折返跑,从球门线出发,向前记为正数,返回记为负数,他的记录如下(单位:米):+5,﹣3,+10,﹣8,﹣6,+12,﹣10,
(1)守门员最后是否回到了球门线的位置?
(2)守门员全部练习结束后,共跑了多少米?
(3)在练习过程中,守门员离开球门线的最远距离是多少米?
21.计算:
(1)2﹣(﹣4)+8÷(﹣2)+(﹣3)
(2)﹣36×(23 + 34 - 112 )
(3)﹣23÷8﹣14 ×(﹣2)2.
22.已知A=3x2﹣x+2y﹣4xy,B=2x2﹣3x﹣y+xy.
(1)化简2A﹣3B;
(2)当x+y=67 ,xy=﹣1,求2A﹣3B的值;
(3)若2A﹣3B的值与y的取值无关,求2A﹣3B的值.
23.数学中,运用整体思想方法在求代数式的值时非常重要.
例如:已知a2+2a=2,则代数式2a2+4a+3=2(a2+2a)+3=2×2+3=7.
请你根据以上材料解答以下问题:
(1)若x2﹣3x=4,求1﹣x2+3x的值.
(2)当x=1时,代数式px3+qx﹣1的值是5,求当x=﹣1时,代数式px3+qx﹣1的值.
(3)当x=2020时,代数式ax5+bx3+cx+6的值为m,直接写出当x=﹣2020时,代数式ax5+bx3+cx+6的值.(用含m的代数式表示)
24.解下列一元一次方程:
(1)2x﹣(x+10)=5x+2(x﹣1);
(2)=.
25.某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个.2个甲种部件和3个乙种部件配成一套,问加工甲乙部件各安排多少人才能使每天加工的甲、乙两种部件刚好配套?
26.在∠AOB和∠COD中,
(1)如图1,已知∠AOB=∠COD=90°,当∠BOD=40°时,求∠AOC的度数;
(2)如图2,已知∠AOB=82°,∠COD=110°,且∠AOC=2∠BOD时,请直接写出∠BOD的度数;
(3)如图3,当∠AOB=α,∠COD=β,且∠AOC=n∠BOD(n>1)时,请直接用含有α,β,n的代数式表示∠BOD的值.
参考答案
一.选择题
1.C; 2.B; 3.A; 4.D; 5.B;
6.B; 7.D; 8.B; 9.A; 10.D;
11.C; 12.D;
二.填空题
13.8;﹣2;
14.﹣4;
15.2或3;
16.﹣2;
17.﹣2;
18.520或560;
19 . 32;
三.解答题
20.解:(1)(+5)+(-3)+(+10)+ (-8) +(-6)+ (+12) + (-10)
= ( 5+10+12 )- ( 3+8+6+10 )
二27- 27
=0 ,
答:守门员最后回到了球门线的位置;
(2) |+5|+-31+1+ 10|+|- 81+1-61+1+12|+1-10|
=5+3+10+8+6+12+ 10
=54 ;
答:守门员全部练习结束后,他共跑了54米;
(3 )由观察可知:在练习过程中,守门员离开球[门线最远距离是12米.
21.解:(1)原式=2+4-4-3=-1 ;
( 2 )原式=-24-27+3=-48 ;
( 3 )原式=-1-1=-2.
22.
解:(1)::A=3x2-x+2y-4xy,B=2x2-3x-y+xy ,
. ..2A-3B
=2 ( 3x2-x+2y-4xy ) -3 ( 2x2-3x-y+xy )
=6x2- 2x +4y- 8xy- 6x2+9x+3y-3xy
=7x+7y-11xy ;
(3) :24A-3B=7x+7y-11xy
=7x+ (7-11x)y,
.:若2A-3B的值与y的取值无关,则7-11x=0 ,
23.
24.
解:(1 )去括号得:2x-x-10=5x+2x-2,
移项得: 2x-x-5x-2x=-2+10 ,
合并得: -6x=8 ,
(2)去分母得:10(3x+2)-20=5(2x-1)-4(2x+1)。
去括号得: 30x+20-20= 10x-5-8x-4,
移项合并得: 28x=-9 ,
25.
解:设安排x人加工甲部件,则安排( 85-x )人加工乙部件,根据题意得
3x16x=2x10x(85-x) ,
解得x=25,
所以85-25=60 (人) ,
答:安排25人加工甲部件, 安排60人加工乙部件.
26.
同课章节目录
