2020-2021学年北师大版七年级下册数学第二章相交线与平行线单元测试卷(Word版,附答案解析)
文档属性
| 名称 | 2020-2021学年北师大版七年级下册数学第二章相交线与平行线单元测试卷(Word版,附答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 138.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 00:00:00 | ||
图片预览

文档简介
2020-2021学年北师大新版七年级下册数学《第2章
相交线与平行线》单元测试卷
一.选择题
1.已知∠β=38°,则∠β的补角等于( )
A.142°
B.132°
C.42°
D.52°
2.如图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中,不正确的是( )
A.点B到AC的垂线段是线段CA
B.CD和AB互相垂直
C.AC与BC互相垂直
D.线段AC的长度是点A到BC的距离
3.下列说法正确的是( )
A.同一个平面内,不相交的两条线段是平行线
B.同一个平面内,两条直线不相交就重合
C.同一个平面内,没有公共点的两条直线是平行线
D.不相交的两条直线是平行线
4.过直线L上一点A,在同一平面内画L的垂线,可以画的条数是( )
A.无数条
B.1
C.2
D.不能确定
5.如图所示,AC⊥BC,AD⊥CD,AB=m,CD=n,则AC的取值范围是( )
A.大于n
B.小于m
C.大于n小于m
D.无法确定
6.若两条平行直线被第三条直线所截,则( )
A.一对同位角的角平分线互相垂直
B.一对内错角的角平分线互相垂直
C.一对同旁内角的角平分线互相平行
D.一对同旁内角的角平分线互相垂直
7.尺规作图所用的作图工具是指( )
A.刻度尺和圆规
B.不带刻度的直尺和圆规
C.刻度尺
D.圆规
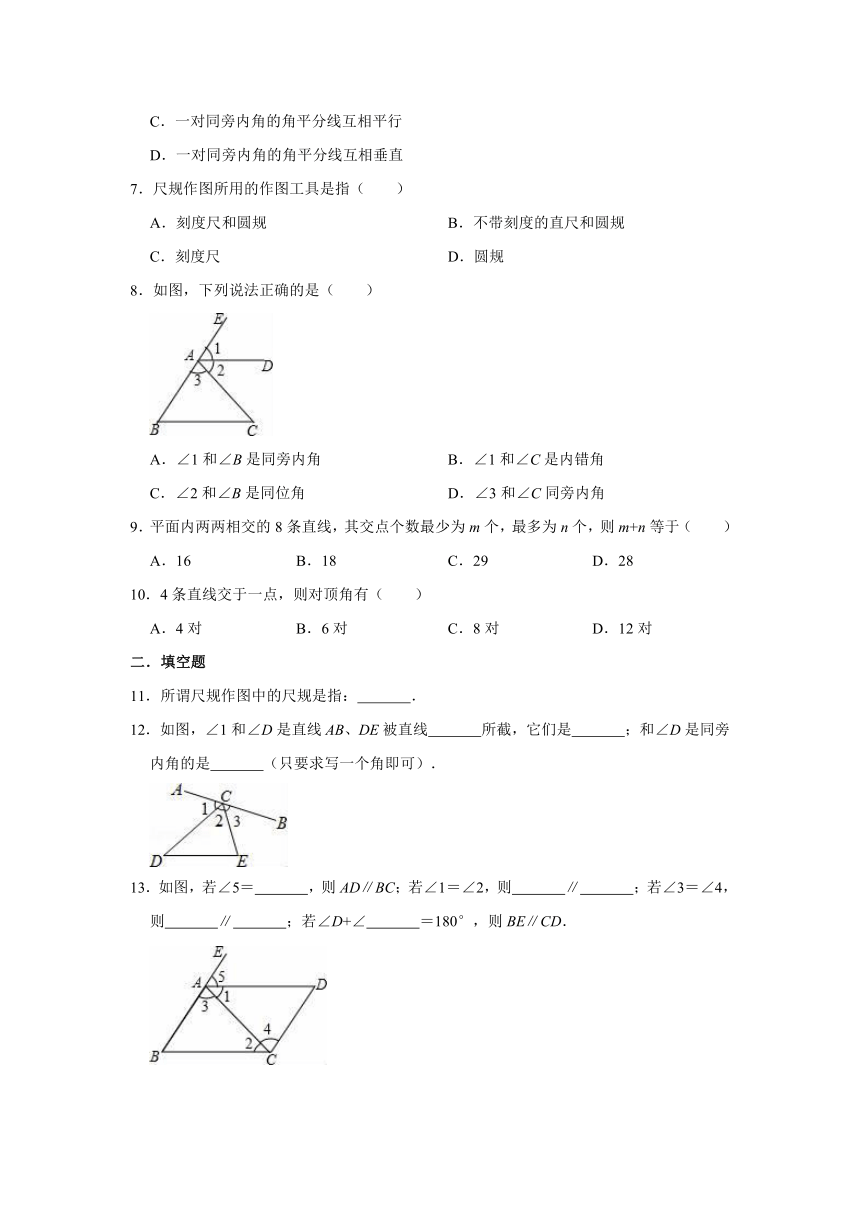
8.如图,下列说法正确的是( )
A.∠1和∠B是同旁内角
B.∠1和∠C是内错角
C.∠2和∠B是同位角
D.∠3和∠C同旁内角
9.平面内两两相交的8条直线,其交点个数最少为m个,最多为n个,则m+n等于( )
A.16
B.18
C.29
D.28
10.4条直线交于一点,则对顶角有( )
A.4对
B.6对
C.8对
D.12对
二.填空题
11.所谓尺规作图中的尺规是指:
.
12.如图,∠1和∠D是直线AB、DE被直线
所截,它们是
;和∠D是同旁内角的是
(只要求写一个角即可).
13.如图,若∠5=
,则AD∥BC;若∠1=∠2,则
∥
;若∠3=∠4,则
∥
;若∠D+∠
=180°,则BE∥CD.
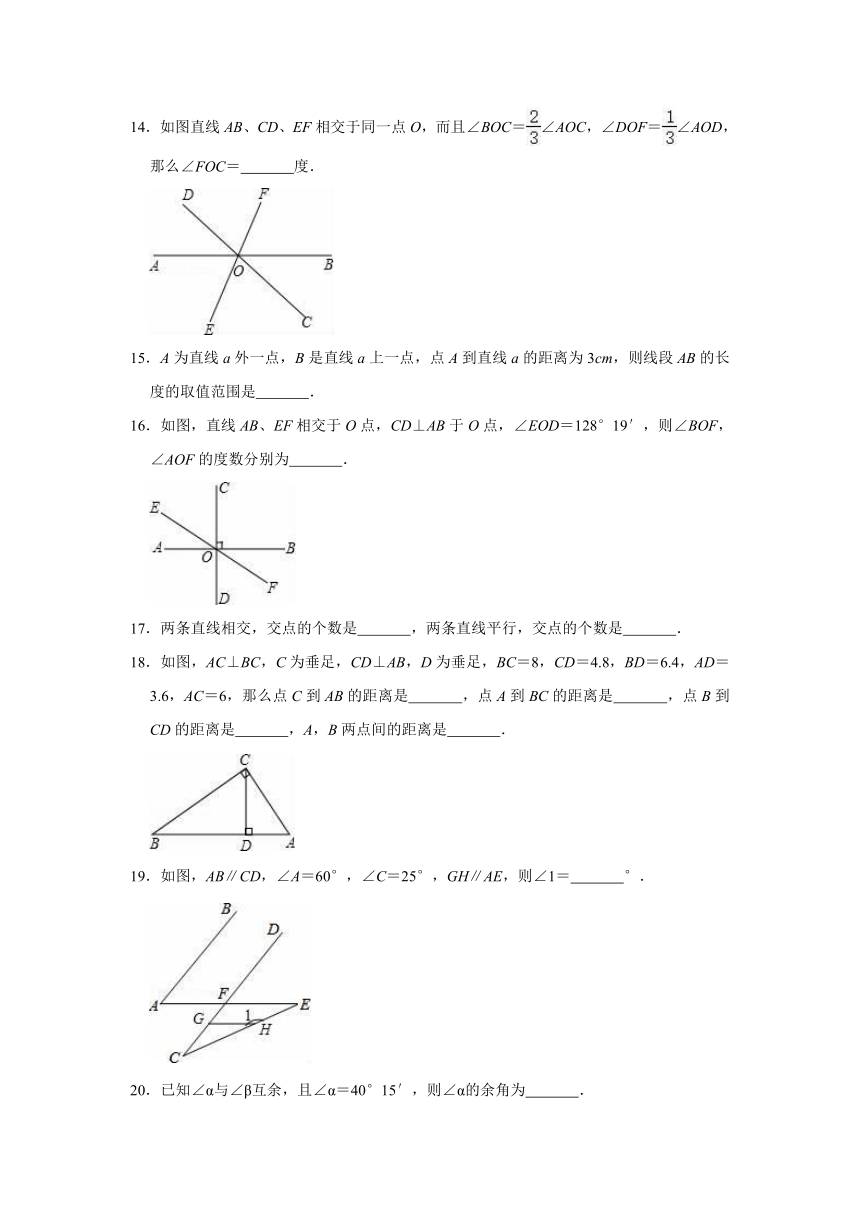
14.如图直线AB、CD、EF相交于同一点O,而且∠BOC=∠AOC,∠DOF=∠AOD,那么∠FOC=
度.
15.A为直线a外一点,B是直线a上一点,点A到直线a的距离为3cm,则线段AB的长度的取值范围是
.
16.如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=128°19′,则∠BOF,∠AOF的度数分别为
.
17.两条直线相交,交点的个数是
,两条直线平行,交点的个数是
.
18.如图,AC⊥BC,C为垂足,CD⊥AB,D为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC=6,那么点C到AB的距离是
,点A到BC的距离是
,点B到CD的距离是
,A,B两点间的距离是
.
19.如图,AB∥CD,∠A=60°,∠C=25°,GH∥AE,则∠1=
°.
20.已知∠α与∠β互余,且∠α=40°15′,则∠α的余角为
.
三.解答题
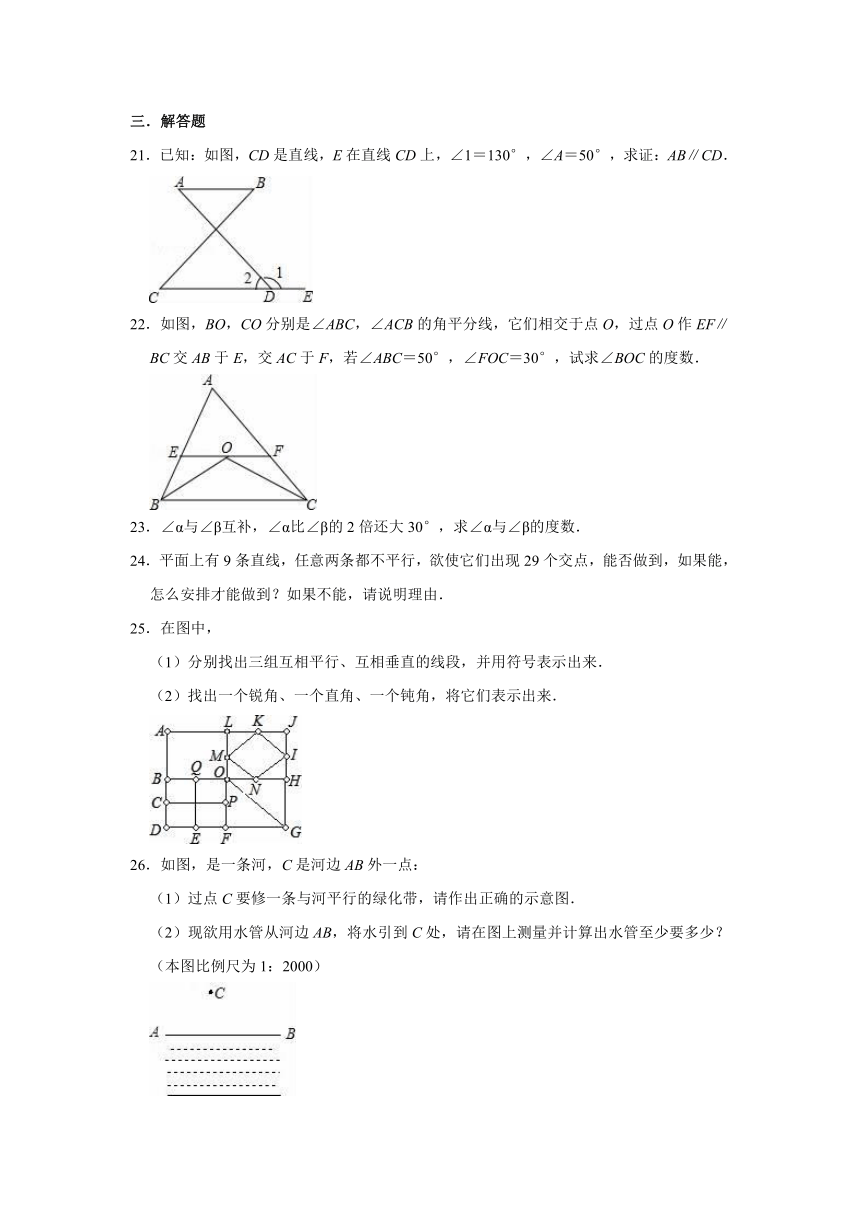
21.已知:如图,CD是直线,E在直线CD上,∠1=130°,∠A=50°,求证:AB∥CD.
22.如图,BO,CO分别是∠ABC,∠ACB的角平分线,它们相交于点O,过点O作EF∥BC交AB于E,交AC于F,若∠ABC=50°,∠FOC=30°,试求∠BOC的度数.
23.∠α与∠β互补,∠α比∠β的2倍还大30°,求∠α与∠β的度数.
24.平面上有9条直线,任意两条都不平行,欲使它们出现29个交点,能否做到,如果能,怎么安排才能做到?如果不能,请说明理由.
25.在图中,
(1)分别找出三组互相平行、互相垂直的线段,并用符号表示出来.
(2)找出一个锐角、一个直角、一个钝角,将它们表示出来.
26.如图,是一条河,C是河边AB外一点:
(1)过点C要修一条与河平行的绿化带,请作出正确的示意图.
(2)现欲用水管从河边AB,将水引到C处,请在图上测量并计算出水管至少要多少?(本图比例尺为1:2000)
参考答案与试题解析
一.选择题
1.解:∠β的补角=180°﹣38°=142°;
故选:A.
2.解:A、∵∠ACB=90°,
∴AC⊥BC,
∴点B到AC的垂线段是线段BC,故本选项错误;
B、∵CD⊥AB,
∴CD和AB互相垂直,故本选项正确;
C、∵∠ACB=90°,
∴AC⊥BC,
∴AC与BC互相垂直,故本选项正确;
D、∵AC⊥BC,
∴线段AC的长度是点A到BC的距离.
故选:A.
3.解:A、应该是不相交的两条直线,故错误;
B、还有平行的情况,故错误;
C、正确;
D、应该是在同一平面内,故错误.
故选:C.
4.解:根据垂线的性质,这样的直线只能作一条.故选B.
5.解:∵AC⊥BC,
∴AC<AB,
∵AD⊥CD,
∴AC>CD,
∴CD<AC<AB,
∵AB=m,CD=n,
∴AC的取值范围是:大于n小于m.
故选:C.
6.解:A、两直线平行,同位角相等,其角平分线分得的角也相等.根据同位角相等,两直线平行可判断角平分线平行,故本选项错误;
B、两直线平行,内错角相等,其角平分线分得的角也相等.根据内错角相等,两直线平行可判断角平分线平行,故本选项错误;
C、两直线平行,同旁内角互补,其角平分线分得的不同的两角互余,从而推出两条角平分线相交成90°角,即互相垂直,故本选项错误;
D、两直线平行,同旁内角互补,其角平分线分得的不同的两角互余,从而推出两条角平分线相交成90°角,即互相垂直,故本选项正确.
故选:D.
7.解:尺规作图所用的作图工具是指不带刻度的直尺和圆规.
故选:B.
8.解:A、∠1和∠B是同位角,故本选项错误;
B、∠1和∠C既不是同位角、内错角,也不是同旁内角,故本选项错误;
C、∠2和∠B既不是同位角、内错角,也不是同旁内角,故本选项错误;
D、∠3和∠C是同旁内角,故本选项正确.
故选:D.
9.解:根据题意可得:8条直线相交于一点时交点最少,此时交点为1个,即m=1;
任意两直线相交都产生一个交点时交点最多,
∵任意三条直线不过同一点,
∴此时交点为:8×(8﹣1)÷2=28,即n=28;
则m+n=29.
故选:C.
10.解:根据对顶角的定义可知:4条直线交于一点,则对顶角有12对.故选D.
二.填空题
11.解:由尺规作图的概念可知:尺规作图中的尺规指的是没有刻度的直尺和圆规.
12.解:根据图示知,∠1和∠D是直线AB、DE被直线CD所截.∠D是同旁内角的是∠2、∠E和∠DCB.
故答案可以是:∠2.
13.解:如图,若∠5=∠B,则AD∥BC;若∠1=∠2,则
AD∥BC;若∠3=∠4,则
AB∥DC;若∠D+∠BAD=180°,则BE∥CD.
故答案是:∠B;AD,BC;AB,CD;BAD.
14.解:∵∠BOC+∠AOC=180°,∠BOC=∠AOC,
∴∠BOC=72°,
∴∠BOC=∠AOD=72°,
∵∠DOF=∠AOD=24°,
∴∠FOC=180°﹣∠DOF=156°.
15.解:∵A为直线a外一点,B是直线a上一点,点A到直线a的距离为3cm,
∴AB最短为3cm.
∴AB≥3cm.
故答案是:AB≥3cm.
16.解:∵CD⊥AB,
∴∠AOD=∠BOC=90°,
∴∠AOE=∠EOD﹣∠AOD=128°19′﹣90°=38°19′.
∴∠BOF=∠AOE=38°19′.
∴∠AOF=180°﹣∠BOF=180°﹣38°19′=141°41′.
17.解:两条直线相交,交点的个数是1,两条直线平行,交点的个数是0.
18.解:点C到直线AB的垂线段是CD,所以线段CD的长是点C到直线AB的距离,即点C到AB的距离是4.8;
点A到直线BC的垂线段是AC,所以线段AC的长是点A到直线BC的距离,即点A到BC的距离是6;
点B到直线CD的垂线段是BD,所以线段BD的长是点B到直线CD的距离,即点B到CD的距离是6.4;
点B到点A的距离是线段AB的长,即点B到点A的距离是10.
故填4.8,6,6.4,10.
19.解:∵AB∥CD,
∴∠DFE=∠A=60°,
∴∠E=∠DFE﹣∠C=60°﹣25°=35°,
∵GH∥AE,
∴∠GHC=∠E=35°,
∴∠1=180°﹣35°=145°;
故答案为:145°.
20.解:∵∠α与∠β互余,
∴∠α+∠β=90°,
∵∠α=40°15′,
∴∠α的余角为90°﹣40°15′=49°45′.
故答案为:49°45′.
三.解答题
21.证明:∵∠1+∠2=180°,∠1=130°,
∴∠2=50°,
∵∠A=50°,
∴∠A=∠2,
∴AB∥CD.
22.解:∵B0是∠ABC的角平分线,
∴∠OBC=∠ABC=25°,
∵EF∥BC,
∴∠EOB=∠OBC=25°,
∴∠BOC=180°﹣25°﹣30°=125°.
23.解:∵∠α与∠β互补,
∴∠α+∠β=180°①,
又∵∠α比∠β的2倍还大30°,
∴∠α=2∠β+30°②,
①②联立,解得∠α=50°,∠β=130°.
答:∠α的度数是50°,∠β的度数是130°.
24.解:能.理由如下:
9条直线,任意两条都不平行,最多交点的个数是==36,
∵36>29,
∴能出现29个交点,
安排如下:先使4条直线相交于一点P,另外5条直线两两相交最多可得=10个交点,
与前四条直线相交最多可得5×4=20个交点,
让其中两个点重合为点O,所以交点减少1个,
交点个数一共有10+20﹣1=29个.
故能做到.
25.解:(1)答案不唯一,如:AD∥LF,AD∥JG,AJ∥DG;AD⊥DG,AD⊥AJ,AJ⊥JG;
(2)答案不唯一,如:锐角∠MNO、直角∠DAJ、钝角∠LOG.
26.解:如图:
(1)过点C画一平行线平行于AB.
(2)过点C作CD垂直于AB交AB于点D.
然后用尺子量CD的长度,再按1:2000的比例求得实际距离即可.
相交线与平行线》单元测试卷
一.选择题
1.已知∠β=38°,则∠β的补角等于( )
A.142°
B.132°
C.42°
D.52°
2.如图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中,不正确的是( )
A.点B到AC的垂线段是线段CA
B.CD和AB互相垂直
C.AC与BC互相垂直
D.线段AC的长度是点A到BC的距离
3.下列说法正确的是( )
A.同一个平面内,不相交的两条线段是平行线
B.同一个平面内,两条直线不相交就重合
C.同一个平面内,没有公共点的两条直线是平行线
D.不相交的两条直线是平行线
4.过直线L上一点A,在同一平面内画L的垂线,可以画的条数是( )
A.无数条
B.1
C.2
D.不能确定
5.如图所示,AC⊥BC,AD⊥CD,AB=m,CD=n,则AC的取值范围是( )
A.大于n
B.小于m
C.大于n小于m
D.无法确定
6.若两条平行直线被第三条直线所截,则( )
A.一对同位角的角平分线互相垂直
B.一对内错角的角平分线互相垂直
C.一对同旁内角的角平分线互相平行
D.一对同旁内角的角平分线互相垂直
7.尺规作图所用的作图工具是指( )
A.刻度尺和圆规
B.不带刻度的直尺和圆规
C.刻度尺
D.圆规
8.如图,下列说法正确的是( )
A.∠1和∠B是同旁内角
B.∠1和∠C是内错角
C.∠2和∠B是同位角
D.∠3和∠C同旁内角
9.平面内两两相交的8条直线,其交点个数最少为m个,最多为n个,则m+n等于( )
A.16
B.18
C.29
D.28
10.4条直线交于一点,则对顶角有( )
A.4对
B.6对
C.8对
D.12对
二.填空题
11.所谓尺规作图中的尺规是指:
.
12.如图,∠1和∠D是直线AB、DE被直线
所截,它们是
;和∠D是同旁内角的是
(只要求写一个角即可).
13.如图,若∠5=
,则AD∥BC;若∠1=∠2,则
∥
;若∠3=∠4,则
∥
;若∠D+∠
=180°,则BE∥CD.
14.如图直线AB、CD、EF相交于同一点O,而且∠BOC=∠AOC,∠DOF=∠AOD,那么∠FOC=
度.
15.A为直线a外一点,B是直线a上一点,点A到直线a的距离为3cm,则线段AB的长度的取值范围是
.
16.如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=128°19′,则∠BOF,∠AOF的度数分别为
.
17.两条直线相交,交点的个数是
,两条直线平行,交点的个数是
.
18.如图,AC⊥BC,C为垂足,CD⊥AB,D为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC=6,那么点C到AB的距离是
,点A到BC的距离是
,点B到CD的距离是
,A,B两点间的距离是
.
19.如图,AB∥CD,∠A=60°,∠C=25°,GH∥AE,则∠1=
°.
20.已知∠α与∠β互余,且∠α=40°15′,则∠α的余角为
.
三.解答题
21.已知:如图,CD是直线,E在直线CD上,∠1=130°,∠A=50°,求证:AB∥CD.
22.如图,BO,CO分别是∠ABC,∠ACB的角平分线,它们相交于点O,过点O作EF∥BC交AB于E,交AC于F,若∠ABC=50°,∠FOC=30°,试求∠BOC的度数.
23.∠α与∠β互补,∠α比∠β的2倍还大30°,求∠α与∠β的度数.
24.平面上有9条直线,任意两条都不平行,欲使它们出现29个交点,能否做到,如果能,怎么安排才能做到?如果不能,请说明理由.
25.在图中,
(1)分别找出三组互相平行、互相垂直的线段,并用符号表示出来.
(2)找出一个锐角、一个直角、一个钝角,将它们表示出来.
26.如图,是一条河,C是河边AB外一点:
(1)过点C要修一条与河平行的绿化带,请作出正确的示意图.
(2)现欲用水管从河边AB,将水引到C处,请在图上测量并计算出水管至少要多少?(本图比例尺为1:2000)
参考答案与试题解析
一.选择题
1.解:∠β的补角=180°﹣38°=142°;
故选:A.
2.解:A、∵∠ACB=90°,
∴AC⊥BC,
∴点B到AC的垂线段是线段BC,故本选项错误;
B、∵CD⊥AB,
∴CD和AB互相垂直,故本选项正确;
C、∵∠ACB=90°,
∴AC⊥BC,
∴AC与BC互相垂直,故本选项正确;
D、∵AC⊥BC,
∴线段AC的长度是点A到BC的距离.
故选:A.
3.解:A、应该是不相交的两条直线,故错误;
B、还有平行的情况,故错误;
C、正确;
D、应该是在同一平面内,故错误.
故选:C.
4.解:根据垂线的性质,这样的直线只能作一条.故选B.
5.解:∵AC⊥BC,
∴AC<AB,
∵AD⊥CD,
∴AC>CD,
∴CD<AC<AB,
∵AB=m,CD=n,
∴AC的取值范围是:大于n小于m.
故选:C.
6.解:A、两直线平行,同位角相等,其角平分线分得的角也相等.根据同位角相等,两直线平行可判断角平分线平行,故本选项错误;
B、两直线平行,内错角相等,其角平分线分得的角也相等.根据内错角相等,两直线平行可判断角平分线平行,故本选项错误;
C、两直线平行,同旁内角互补,其角平分线分得的不同的两角互余,从而推出两条角平分线相交成90°角,即互相垂直,故本选项错误;
D、两直线平行,同旁内角互补,其角平分线分得的不同的两角互余,从而推出两条角平分线相交成90°角,即互相垂直,故本选项正确.
故选:D.
7.解:尺规作图所用的作图工具是指不带刻度的直尺和圆规.
故选:B.
8.解:A、∠1和∠B是同位角,故本选项错误;
B、∠1和∠C既不是同位角、内错角,也不是同旁内角,故本选项错误;
C、∠2和∠B既不是同位角、内错角,也不是同旁内角,故本选项错误;
D、∠3和∠C是同旁内角,故本选项正确.
故选:D.
9.解:根据题意可得:8条直线相交于一点时交点最少,此时交点为1个,即m=1;
任意两直线相交都产生一个交点时交点最多,
∵任意三条直线不过同一点,
∴此时交点为:8×(8﹣1)÷2=28,即n=28;
则m+n=29.
故选:C.
10.解:根据对顶角的定义可知:4条直线交于一点,则对顶角有12对.故选D.
二.填空题
11.解:由尺规作图的概念可知:尺规作图中的尺规指的是没有刻度的直尺和圆规.
12.解:根据图示知,∠1和∠D是直线AB、DE被直线CD所截.∠D是同旁内角的是∠2、∠E和∠DCB.
故答案可以是:∠2.
13.解:如图,若∠5=∠B,则AD∥BC;若∠1=∠2,则
AD∥BC;若∠3=∠4,则
AB∥DC;若∠D+∠BAD=180°,则BE∥CD.
故答案是:∠B;AD,BC;AB,CD;BAD.
14.解:∵∠BOC+∠AOC=180°,∠BOC=∠AOC,
∴∠BOC=72°,
∴∠BOC=∠AOD=72°,
∵∠DOF=∠AOD=24°,
∴∠FOC=180°﹣∠DOF=156°.
15.解:∵A为直线a外一点,B是直线a上一点,点A到直线a的距离为3cm,
∴AB最短为3cm.
∴AB≥3cm.
故答案是:AB≥3cm.
16.解:∵CD⊥AB,
∴∠AOD=∠BOC=90°,
∴∠AOE=∠EOD﹣∠AOD=128°19′﹣90°=38°19′.
∴∠BOF=∠AOE=38°19′.
∴∠AOF=180°﹣∠BOF=180°﹣38°19′=141°41′.
17.解:两条直线相交,交点的个数是1,两条直线平行,交点的个数是0.
18.解:点C到直线AB的垂线段是CD,所以线段CD的长是点C到直线AB的距离,即点C到AB的距离是4.8;
点A到直线BC的垂线段是AC,所以线段AC的长是点A到直线BC的距离,即点A到BC的距离是6;
点B到直线CD的垂线段是BD,所以线段BD的长是点B到直线CD的距离,即点B到CD的距离是6.4;
点B到点A的距离是线段AB的长,即点B到点A的距离是10.
故填4.8,6,6.4,10.
19.解:∵AB∥CD,
∴∠DFE=∠A=60°,
∴∠E=∠DFE﹣∠C=60°﹣25°=35°,
∵GH∥AE,
∴∠GHC=∠E=35°,
∴∠1=180°﹣35°=145°;
故答案为:145°.
20.解:∵∠α与∠β互余,
∴∠α+∠β=90°,
∵∠α=40°15′,
∴∠α的余角为90°﹣40°15′=49°45′.
故答案为:49°45′.
三.解答题
21.证明:∵∠1+∠2=180°,∠1=130°,
∴∠2=50°,
∵∠A=50°,
∴∠A=∠2,
∴AB∥CD.
22.解:∵B0是∠ABC的角平分线,
∴∠OBC=∠ABC=25°,
∵EF∥BC,
∴∠EOB=∠OBC=25°,
∴∠BOC=180°﹣25°﹣30°=125°.
23.解:∵∠α与∠β互补,
∴∠α+∠β=180°①,
又∵∠α比∠β的2倍还大30°,
∴∠α=2∠β+30°②,
①②联立,解得∠α=50°,∠β=130°.
答:∠α的度数是50°,∠β的度数是130°.
24.解:能.理由如下:
9条直线,任意两条都不平行,最多交点的个数是==36,
∵36>29,
∴能出现29个交点,
安排如下:先使4条直线相交于一点P,另外5条直线两两相交最多可得=10个交点,
与前四条直线相交最多可得5×4=20个交点,
让其中两个点重合为点O,所以交点减少1个,
交点个数一共有10+20﹣1=29个.
故能做到.
25.解:(1)答案不唯一,如:AD∥LF,AD∥JG,AJ∥DG;AD⊥DG,AD⊥AJ,AJ⊥JG;
(2)答案不唯一,如:锐角∠MNO、直角∠DAJ、钝角∠LOG.
26.解:如图:
(1)过点C画一平行线平行于AB.
(2)过点C作CD垂直于AB交AB于点D.
然后用尺子量CD的长度,再按1:2000的比例求得实际距离即可.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
