2020-2021学年苏科版七年级数学下册7.3图形的平移同步习题(Word版,附答案解析)
文档属性
| 名称 | 2020-2021学年苏科版七年级数学下册7.3图形的平移同步习题(Word版,附答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 749.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 23:22:12 | ||
图片预览

文档简介
7.3图形的平移 同步习题
一.选择题
1.下列图案中,可由如图图案平移得到的是( )
A. B. C. D.
2.如图,将周长为7的△ABC沿BC方向平移2个单位得到△DEF,则四边形ABFD的周长为( )
A.16 B.9 C.11 D.12
3.下列现象中,属于平移的是( )
①小朋友在荡秋千;
②打气筒打气时,活塞的运动;
③钟摆的摆动;
④瓶装饮料在传送带上移动.
A.①② B.①③ C.②③ D.②④
4.如图,△ABC沿直线m向右平移a厘米,得到△DEF,下列说法错误的是( )
A.AC∥DF B.CF∥AB C.CF=a厘米 D.DE=a厘米
5.如图,△ABC沿AB方向向右平移后到达△A1B1C1的位置,BC与A1C1相交于点O,若∠C的度数为x,则∠A1OC的度数为( )
A.x B.90°﹣x C.180°﹣x D.90°+x
6.如图,△ABC沿着由点B到点E的方向,平移到△DEF.若BC=5,EC=3,则平移的距离为( )
A.7 B.5 C.3 D.2
7.如图,两个形状、大小完全相同的三角形ABC和三角形DEF重叠在一起,固定三角形ABC不动,将三角形DEF向右平移,当点E和点C重合时,停止移动,设DE交AC于G.给出下列结论:
①四边形ABEG的面积与CGDF的面积相等;
②AD∥EC,且AD=EC,
则( )
A.①,②都正确 B.①正确,②错误
C.①,②都错误 D.①错误,②正确
8.身高1.62米的小明乘升降电梯从1楼上升到3楼,则此时小明的身高为( )
A.1.62米 B.2.62米 C.3.62米 D.4.62米
9.如图,将△ABC沿直线AB向右平移后到达△BDE的位置,连接CD、CE,若△ACD的面积为10,则△BCE的面积为( )
A.5 B.6 C.10 D.4
10.如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路(图中阴影部分),余下部分绿化,小路的宽为2m,则两条小路的总面积是( )m2
A.108 B.104 C.100 D.98
二.填空题
11.已知线段AB的长度为3厘米,现将线段AB向左平移4厘米得到线段CD,那么线段CD的长度为 厘米.
12.如图,将三角形ABC沿水平方向向右平移到三角形DEF的位置,若BF=11,EC=5,则A,D之间的距离为 .
13.如图是用三角尺和直尺画平行线的示意图,将三角尺ABC沿着直尺PQ平移到三角尺A′B′C′的位置,就可以画出AB的平行线A′B′.若AC′=9cm,A′C=2cm,则直线AB平移的距离为 cm.
14.如图,直线m与∠AOB的一边射线OB相交,∠1=30°,向上平移直线m得到直线n,与∠AOB的另一边射线OA相交,则∠2+∠3= .
15.如图,将△ABC沿着某一方向平移一定的距离得到△DEF,则下列结论:
①AD∥CF;
②AC=DF;
③∠ABC=∠DFE;
④∠DAE=∠AEB.
正确有 (填序号即可).
三.解答题
16.如图,将△ABC,向右平移4个格子,再向下平移2个格子.
(1)请你画出经过两次平移后的△DEF(A与D、B与E、C与F对应);
(2)若每个小正方形的边长为1个单位长度,连接BE和CE,请你求出△BCE的面积.
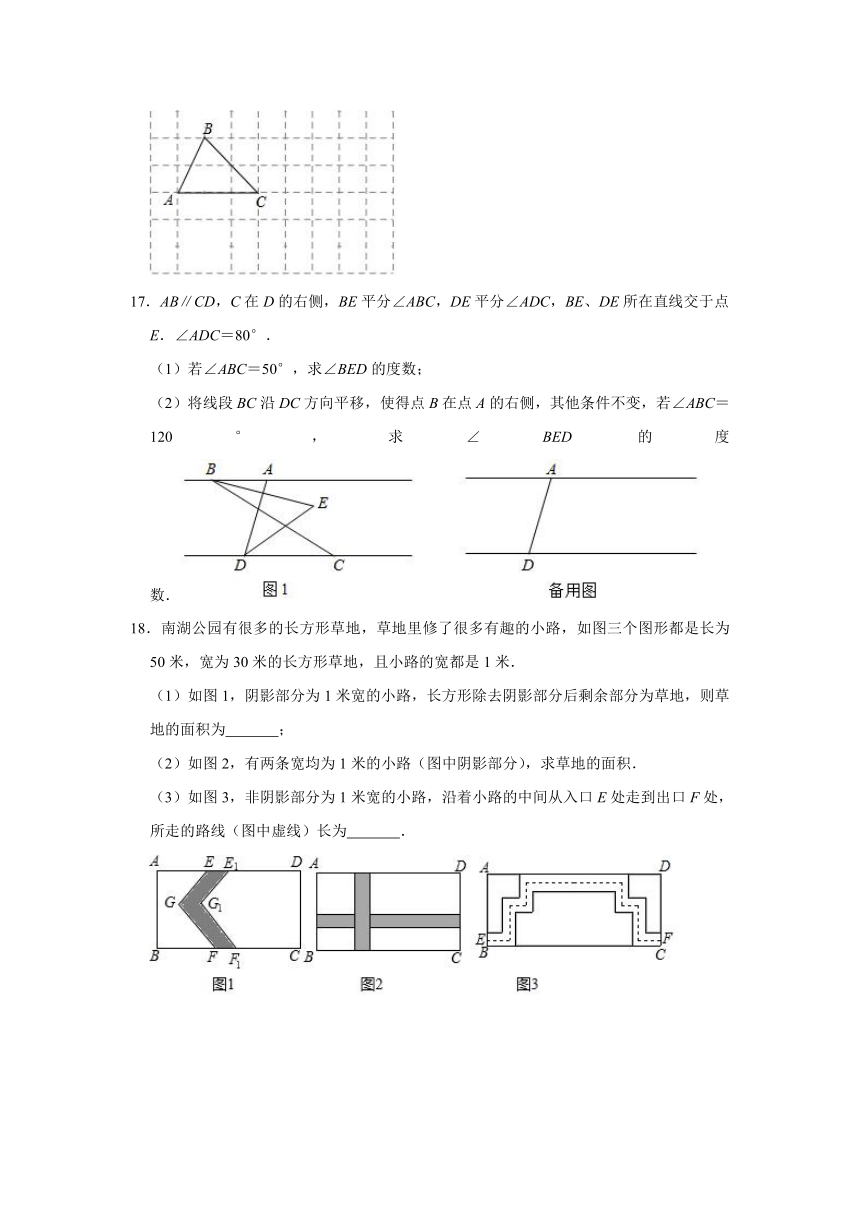
17.AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC=80°.
(1)若∠ABC=50°,求∠BED的度数;
(2)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,若∠ABC=120°,求∠BED的度数.
18.南湖公园有很多的长方形草地,草地里修了很多有趣的小路,如图三个图形都是长为50米,宽为30米的长方形草地,且小路的宽都是1米.
(1)如图1,阴影部分为1米宽的小路,长方形除去阴影部分后剩余部分为草地,则草地的面积为 ;
(2)如图2,有两条宽均为1米的小路(图中阴影部分),求草地的面积.
(3)如图3,非阴影部分为1米宽的小路,沿着小路的中间从入口E处走到出口F处,所走的路线(图中虚线)长为 .
参考答案
一.选择题
1.解:观察各选项图形可知,D选项的图案可以通过平移得到.
故选:D.
2.解:∵△ABC沿BC方向平移2个单位得到△DEF,
∴AC=DF,AD=CF=2,
∵△ABC的周长为7,
∴AB+BC+AC=7,
∴四边形ABFD的周长=AB+BF+DF+AD=AB+BC+CF+AC+AD=7+CF+AD=7+2+2=11.
故选:C.
3.解:①小朋友在荡秋千是旋转,不属于平移;
②打气筒打气时,活塞的运动,属于平移;
③钟摆的摆动是旋转,不属于平移;
④瓶装饮料在传送带上移动,属于平移.
故选:D.
4.解:∵△ABC沿直线m向右平移a厘米,得到△DEF,
∴AC∥DF,CF∥AB,CF=AD=BE=a厘米.
故选:D.
5.解:∵△ABC沿AB方向向右平移后到达△A1B1C1的位置,BC与A1C1相交于点O,
∴∠C1=∠C,BC∥B1C1,
∴∠COC1=∠C1,
∴∠A1OC=180°﹣x,
故选:C.
6.解:由题意得平移的距离为:BE=BC﹣EC=5﹣3=2,
故选:D.
7.解:由平移可得:△ABC的面积=△DEF的面积,
所以△ABC的面积﹣△EGC的面积=△DEF的面积﹣△EGC的面积,
即四边形ABEG的面积与CGDF的面积相等,故①正确;
由平移可得:AD∥EC,AD=BE,故②错误;
故选:B.
8.解:身高1.62米的小明乘升降电梯从1楼上升到3楼,则此时小明的身高为1.62米,
故选:A.
9.解:∵△ABC沿直线AB向右平移后到达△BDE的位置,
∴AB=BD,BC∥DE,
∴S△ABC=S△BCD=S△ACD=×10=5,
∵DE∥BC,
∴S△BCE=S△BCD=5.
故选:A.
10.解:利用平移可得,两条小路的总面积是:30×22﹣(30﹣2)(22﹣2)=100(m2).
故选:C.
二.填空题
11.解:经过平移,对应点所连的线段平行且相等,对应线段平行且相等.将线段AB向左平移4厘米得到线段CD,
则AB=CD=3厘米.
故答案为:3.
12.解:∵三角形ABC沿水平方向向右平移到三角形DEF的位置,
∴AD=BE=CF,
∵BF=BE+EC+CF,
∴BE=(11﹣5)=3,
∴AD=3.
故答案为:3.
13.解:AC+A′C′=AC′﹣A′C=9﹣2=7(cm),
A′C′=7÷2=3.5(cm),
CC′=A′C+A′C′=2+3.5=5.5(cm).
故直线AB平移的距离为5.5cm.
故答案为:5.5.
14.解:作OC∥m,如图,
∵直线m向上平移直线m得到直线n,
∴m∥n,
∴OC∥n,
∴∠1=∠OBC=30°,∠2+∠AOC=180°,
∴∠2+∠3=180°+30°=210°.
故答案为210°.
15.解:∵△ABC沿着某一方向平移一定的距离得到△DEF,
∴①AD∥CF,正确;
②AC=DF,正确;
③∠ABC=∠DEF,故原命题错误;
④∠DAE=∠AEB,正确.
所以,正确的有①②④.
故答案为:①②④.
三.解答题
16.解:(1)如图,△DEF即为所求.
(2)S△BCE=×2×2=2.
17.解:(1)作EF∥AB,如图1,
∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠ABC=25°,∠EDC=∠ADC=40°,
∵AB∥CD,
∴EF∥CD,
∵∠BEF=∠ABE=25°,∠FED=∠EDC=40°,
∴∠BED=25°+40°=65°;
(2)作EF∥AB,如图2,
∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠ABC=60°,∠EDC=∠ADC=40°,
∵AB∥CD,
∴EF∥CD,
∵∠BEF=180°﹣∠ABE=120°,∠FED=∠EDC=40°,
∴∠BED=120°+40°=160°.
18.解:(1)将小路往左平移,直到E、F与A、B重合,则平移后的四边形EFF1E1是一个矩形,并且EF=AB=30,FF1=EE1=1,
则草地的面积为:50×30﹣1×30=1470(平方米);
故答案为:1470平方米;
(2)小路往AB、AD边平移,直到小路与草地的边重合,
则草地的面积为:(50﹣1)×(30﹣1)=1421(平方米);
(3)将小路往AB、AD、DC边平移,直到小路与草地的边重合,
则所走的路线(图中虚线)长为:30﹣1+50+30﹣1=108(米).
故答案为:108米.
一.选择题
1.下列图案中,可由如图图案平移得到的是( )
A. B. C. D.
2.如图,将周长为7的△ABC沿BC方向平移2个单位得到△DEF,则四边形ABFD的周长为( )
A.16 B.9 C.11 D.12
3.下列现象中,属于平移的是( )
①小朋友在荡秋千;
②打气筒打气时,活塞的运动;
③钟摆的摆动;
④瓶装饮料在传送带上移动.
A.①② B.①③ C.②③ D.②④
4.如图,△ABC沿直线m向右平移a厘米,得到△DEF,下列说法错误的是( )
A.AC∥DF B.CF∥AB C.CF=a厘米 D.DE=a厘米
5.如图,△ABC沿AB方向向右平移后到达△A1B1C1的位置,BC与A1C1相交于点O,若∠C的度数为x,则∠A1OC的度数为( )
A.x B.90°﹣x C.180°﹣x D.90°+x
6.如图,△ABC沿着由点B到点E的方向,平移到△DEF.若BC=5,EC=3,则平移的距离为( )
A.7 B.5 C.3 D.2
7.如图,两个形状、大小完全相同的三角形ABC和三角形DEF重叠在一起,固定三角形ABC不动,将三角形DEF向右平移,当点E和点C重合时,停止移动,设DE交AC于G.给出下列结论:
①四边形ABEG的面积与CGDF的面积相等;
②AD∥EC,且AD=EC,
则( )
A.①,②都正确 B.①正确,②错误
C.①,②都错误 D.①错误,②正确
8.身高1.62米的小明乘升降电梯从1楼上升到3楼,则此时小明的身高为( )
A.1.62米 B.2.62米 C.3.62米 D.4.62米
9.如图,将△ABC沿直线AB向右平移后到达△BDE的位置,连接CD、CE,若△ACD的面积为10,则△BCE的面积为( )
A.5 B.6 C.10 D.4
10.如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路(图中阴影部分),余下部分绿化,小路的宽为2m,则两条小路的总面积是( )m2
A.108 B.104 C.100 D.98
二.填空题
11.已知线段AB的长度为3厘米,现将线段AB向左平移4厘米得到线段CD,那么线段CD的长度为 厘米.
12.如图,将三角形ABC沿水平方向向右平移到三角形DEF的位置,若BF=11,EC=5,则A,D之间的距离为 .
13.如图是用三角尺和直尺画平行线的示意图,将三角尺ABC沿着直尺PQ平移到三角尺A′B′C′的位置,就可以画出AB的平行线A′B′.若AC′=9cm,A′C=2cm,则直线AB平移的距离为 cm.
14.如图,直线m与∠AOB的一边射线OB相交,∠1=30°,向上平移直线m得到直线n,与∠AOB的另一边射线OA相交,则∠2+∠3= .
15.如图,将△ABC沿着某一方向平移一定的距离得到△DEF,则下列结论:
①AD∥CF;
②AC=DF;
③∠ABC=∠DFE;
④∠DAE=∠AEB.
正确有 (填序号即可).
三.解答题
16.如图,将△ABC,向右平移4个格子,再向下平移2个格子.
(1)请你画出经过两次平移后的△DEF(A与D、B与E、C与F对应);
(2)若每个小正方形的边长为1个单位长度,连接BE和CE,请你求出△BCE的面积.
17.AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC=80°.
(1)若∠ABC=50°,求∠BED的度数;
(2)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,若∠ABC=120°,求∠BED的度数.
18.南湖公园有很多的长方形草地,草地里修了很多有趣的小路,如图三个图形都是长为50米,宽为30米的长方形草地,且小路的宽都是1米.
(1)如图1,阴影部分为1米宽的小路,长方形除去阴影部分后剩余部分为草地,则草地的面积为 ;
(2)如图2,有两条宽均为1米的小路(图中阴影部分),求草地的面积.
(3)如图3,非阴影部分为1米宽的小路,沿着小路的中间从入口E处走到出口F处,所走的路线(图中虚线)长为 .
参考答案
一.选择题
1.解:观察各选项图形可知,D选项的图案可以通过平移得到.
故选:D.
2.解:∵△ABC沿BC方向平移2个单位得到△DEF,
∴AC=DF,AD=CF=2,
∵△ABC的周长为7,
∴AB+BC+AC=7,
∴四边形ABFD的周长=AB+BF+DF+AD=AB+BC+CF+AC+AD=7+CF+AD=7+2+2=11.
故选:C.
3.解:①小朋友在荡秋千是旋转,不属于平移;
②打气筒打气时,活塞的运动,属于平移;
③钟摆的摆动是旋转,不属于平移;
④瓶装饮料在传送带上移动,属于平移.
故选:D.
4.解:∵△ABC沿直线m向右平移a厘米,得到△DEF,
∴AC∥DF,CF∥AB,CF=AD=BE=a厘米.
故选:D.
5.解:∵△ABC沿AB方向向右平移后到达△A1B1C1的位置,BC与A1C1相交于点O,
∴∠C1=∠C,BC∥B1C1,
∴∠COC1=∠C1,
∴∠A1OC=180°﹣x,
故选:C.
6.解:由题意得平移的距离为:BE=BC﹣EC=5﹣3=2,
故选:D.
7.解:由平移可得:△ABC的面积=△DEF的面积,
所以△ABC的面积﹣△EGC的面积=△DEF的面积﹣△EGC的面积,
即四边形ABEG的面积与CGDF的面积相等,故①正确;
由平移可得:AD∥EC,AD=BE,故②错误;
故选:B.
8.解:身高1.62米的小明乘升降电梯从1楼上升到3楼,则此时小明的身高为1.62米,
故选:A.
9.解:∵△ABC沿直线AB向右平移后到达△BDE的位置,
∴AB=BD,BC∥DE,
∴S△ABC=S△BCD=S△ACD=×10=5,
∵DE∥BC,
∴S△BCE=S△BCD=5.
故选:A.
10.解:利用平移可得,两条小路的总面积是:30×22﹣(30﹣2)(22﹣2)=100(m2).
故选:C.
二.填空题
11.解:经过平移,对应点所连的线段平行且相等,对应线段平行且相等.将线段AB向左平移4厘米得到线段CD,
则AB=CD=3厘米.
故答案为:3.
12.解:∵三角形ABC沿水平方向向右平移到三角形DEF的位置,
∴AD=BE=CF,
∵BF=BE+EC+CF,
∴BE=(11﹣5)=3,
∴AD=3.
故答案为:3.
13.解:AC+A′C′=AC′﹣A′C=9﹣2=7(cm),
A′C′=7÷2=3.5(cm),
CC′=A′C+A′C′=2+3.5=5.5(cm).
故直线AB平移的距离为5.5cm.
故答案为:5.5.
14.解:作OC∥m,如图,
∵直线m向上平移直线m得到直线n,
∴m∥n,
∴OC∥n,
∴∠1=∠OBC=30°,∠2+∠AOC=180°,
∴∠2+∠3=180°+30°=210°.
故答案为210°.
15.解:∵△ABC沿着某一方向平移一定的距离得到△DEF,
∴①AD∥CF,正确;
②AC=DF,正确;
③∠ABC=∠DEF,故原命题错误;
④∠DAE=∠AEB,正确.
所以,正确的有①②④.
故答案为:①②④.
三.解答题
16.解:(1)如图,△DEF即为所求.
(2)S△BCE=×2×2=2.
17.解:(1)作EF∥AB,如图1,
∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠ABC=25°,∠EDC=∠ADC=40°,
∵AB∥CD,
∴EF∥CD,
∵∠BEF=∠ABE=25°,∠FED=∠EDC=40°,
∴∠BED=25°+40°=65°;
(2)作EF∥AB,如图2,
∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠ABC=60°,∠EDC=∠ADC=40°,
∵AB∥CD,
∴EF∥CD,
∵∠BEF=180°﹣∠ABE=120°,∠FED=∠EDC=40°,
∴∠BED=120°+40°=160°.
18.解:(1)将小路往左平移,直到E、F与A、B重合,则平移后的四边形EFF1E1是一个矩形,并且EF=AB=30,FF1=EE1=1,
则草地的面积为:50×30﹣1×30=1470(平方米);
故答案为:1470平方米;
(2)小路往AB、AD边平移,直到小路与草地的边重合,
则草地的面积为:(50﹣1)×(30﹣1)=1421(平方米);
(3)将小路往AB、AD、DC边平移,直到小路与草地的边重合,
则所走的路线(图中虚线)长为:30﹣1+50+30﹣1=108(米).
故答案为:108米.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
