直角三角形的判定(1)课件
图片预览






文档简介
(共15张PPT)
直角三角形有哪些性质?
(1)有一个角是直角;
(2)两个锐角的和为90°(互余 );
(3)两直角边的平方和等于斜边的平方 ;
反之,一个三角形满足什么条件,
才能是直角三角形呢
回顾
思考:
(1)有一个角是直角的三角形是直角三角形;
(2)有两个角的和是90°的三角形是直角三角形;
(3)如果一个三角形的三边a ,b ,c 满足a2 +b 2=c2 ,
那么这个三角形是直角三角形
一个三角形应满足什么条件才能是直角三角形
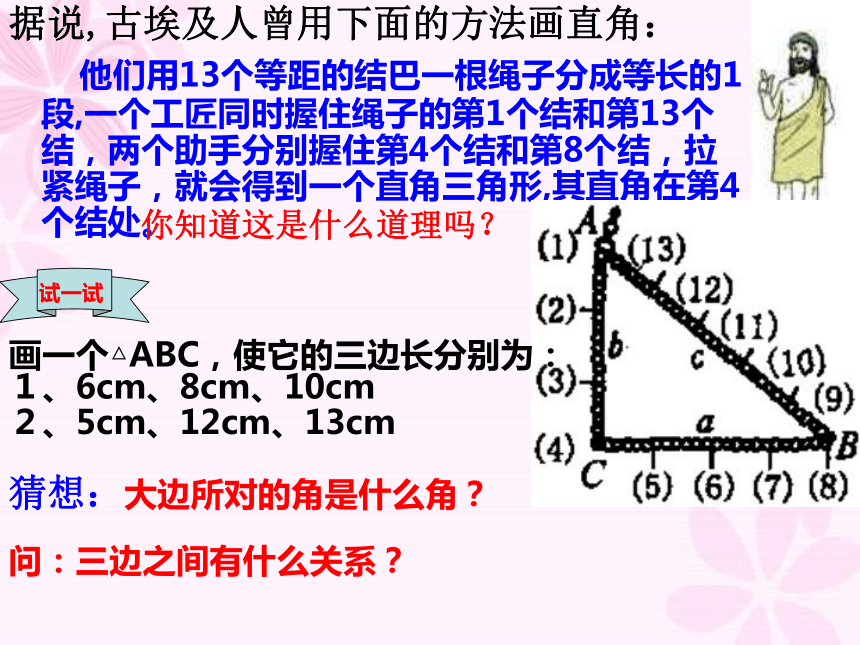
据说,古埃及人曾用下面的方法画直角:
他们用13个等距的结巴一根绳子分成等长的1段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处。
试一试
画一个△ABC,使它的三边长分别为:
1、6cm、8cm、10cm
2、5cm、12cm、13cm
猜想:大边所对的角是什么角?
问:三边之间有什么关系?
你知道这是什么道理吗?
勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么 。
a2 + b2 = c2
勾股定理逆定理:如果三角形的三边长a、b、c满足 ,那么这个三角形是直角三角形。
a2 + b2 = c2
反过来
分析:根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较短边长的平方和是否等于最长的边的平方.
例1:判断由线段a,b,c组成的三角形是不是直角
三角形
(1) a=15,b=17,c=8; (2) a=13,b=15,c=14
解:(1)最大边为17
∵152+82=225+64 =289
172 =289
∴152+82 =172
∴以15, 8, 17为边长的三角形是直角三角形
(2)最大边为15
∵132+142=169+196=365
152 =225
∴132+ 142 ≠ 152
∴以13, 15, 14为边长的三角形不是直角三角形
像15,17,8,能够成为直角三角形三条边长的三个正整数,称为勾股数.
∠C=900
(3) a=1 b=2 c= ____ _____ ;
下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
(1) a=25 b=20 c=15 ____ _____ ;
(2) a=13 b=14 c=15 ____ _____ ;
(4) a=9 b=40 c=41 _____ _____ ;
是
是
不是
是
∠A=900
∠B=900
归纳:
用勾股定理逆定理判断三角形是否是直角三角形的步骤
①、确定最大边(如c,c边所对的角是∠C)
②、验证:c2与a2+b2是否相等
若
则△ABC是以∠C=90°的直角三角形
若
则△ABC不是直角三角形。
直角三角形
较短的两条边的平方和_______最长边的平方
最长边所对的角是______
直角三角形
较短的两条边的平方和______最长边的平方
最长边所对的角是______
(1)
(2)
等于
直角
等于
直角
想一想:
锐角三角形
较短的两条边的平方和 ______最长边的平方
最长边所对的角是______
钝角三角形
较短的两条边的平方和_____最长边的平方
最长边所对的角是________
(3)
(4)
大于
小于
锐角
钝角
∵ S △ ABC= AC AB = BC AD
∴ AD=
例2已知:在△ ABC中, AB=3cm,AC=4cm,
BC=5cm,AD是BC边上的高。求:AD的长。
解: ∵ AB=3cm,AC=4cm, BC=5cm
∴ AB2+AC2=9+16=25
BC2=25
∴ AB2+AC2=BC2
∴ ∠ BAC=900 (勾股定理的逆定理)
3
4
5
A
B
C
D
小结:
直角三角形的判定方法:
1、定义(角):有一个角是90°的三角形是直角三 角形。
3、勾股定理的逆定理(边):如果三角形的三边长a、b、c(c为最大边)满足
则,这个三角形是直角三角形
2、有两个角的和是90°的三角形是直角三角形;
一、判断题. 1. ABC的两边AB=5,AC=12,则BC=13 ( )
2. ABC的a=6,b=8,则c=10 ( )
巩固练习:
二、选择题
1.满足下列条件△ABC,不是直角三角形的是( )
A.b2=a2-c2 B. a:b:c=3:4:5
C.∠C=∠A-∠B D.∠A:∠B :∠C =3:4:5
D
2.下列各组线段中,能组成直角三角形的是( )
A. 5,6,7 B. 32,42,52
C. 5,11,12 D. 5,12,13
D
巩固练习:
3.三角形三边长a、b、c满足条件
则此三角形是( )
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等边三角形
B
1、已知:在△ABC中, AB=15cm,AC=20cm,
BC=25cm,AD是BC边上的高。求: AD的长。
作业:
一:课堂作业
直角三角形有哪些性质?
(1)有一个角是直角;
(2)两个锐角的和为90°(互余 );
(3)两直角边的平方和等于斜边的平方 ;
反之,一个三角形满足什么条件,
才能是直角三角形呢
回顾
思考:
(1)有一个角是直角的三角形是直角三角形;
(2)有两个角的和是90°的三角形是直角三角形;
(3)如果一个三角形的三边a ,b ,c 满足a2 +b 2=c2 ,
那么这个三角形是直角三角形
一个三角形应满足什么条件才能是直角三角形
据说,古埃及人曾用下面的方法画直角:
他们用13个等距的结巴一根绳子分成等长的1段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处。
试一试
画一个△ABC,使它的三边长分别为:
1、6cm、8cm、10cm
2、5cm、12cm、13cm
猜想:大边所对的角是什么角?
问:三边之间有什么关系?
你知道这是什么道理吗?
勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么 。
a2 + b2 = c2
勾股定理逆定理:如果三角形的三边长a、b、c满足 ,那么这个三角形是直角三角形。
a2 + b2 = c2
反过来
分析:根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较短边长的平方和是否等于最长的边的平方.
例1:判断由线段a,b,c组成的三角形是不是直角
三角形
(1) a=15,b=17,c=8; (2) a=13,b=15,c=14
解:(1)最大边为17
∵152+82=225+64 =289
172 =289
∴152+82 =172
∴以15, 8, 17为边长的三角形是直角三角形
(2)最大边为15
∵132+142=169+196=365
152 =225
∴132+ 142 ≠ 152
∴以13, 15, 14为边长的三角形不是直角三角形
像15,17,8,能够成为直角三角形三条边长的三个正整数,称为勾股数.
∠C=900
(3) a=1 b=2 c= ____ _____ ;
下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
(1) a=25 b=20 c=15 ____ _____ ;
(2) a=13 b=14 c=15 ____ _____ ;
(4) a=9 b=40 c=41 _____ _____ ;
是
是
不是
是
∠A=900
∠B=900
归纳:
用勾股定理逆定理判断三角形是否是直角三角形的步骤
①、确定最大边(如c,c边所对的角是∠C)
②、验证:c2与a2+b2是否相等
若
则△ABC是以∠C=90°的直角三角形
若
则△ABC不是直角三角形。
直角三角形
较短的两条边的平方和_______最长边的平方
最长边所对的角是______
直角三角形
较短的两条边的平方和______最长边的平方
最长边所对的角是______
(1)
(2)
等于
直角
等于
直角
想一想:
锐角三角形
较短的两条边的平方和 ______最长边的平方
最长边所对的角是______
钝角三角形
较短的两条边的平方和_____最长边的平方
最长边所对的角是________
(3)
(4)
大于
小于
锐角
钝角
∵ S △ ABC= AC AB = BC AD
∴ AD=
例2已知:在△ ABC中, AB=3cm,AC=4cm,
BC=5cm,AD是BC边上的高。求:AD的长。
解: ∵ AB=3cm,AC=4cm, BC=5cm
∴ AB2+AC2=9+16=25
BC2=25
∴ AB2+AC2=BC2
∴ ∠ BAC=900 (勾股定理的逆定理)
3
4
5
A
B
C
D
小结:
直角三角形的判定方法:
1、定义(角):有一个角是90°的三角形是直角三 角形。
3、勾股定理的逆定理(边):如果三角形的三边长a、b、c(c为最大边)满足
则,这个三角形是直角三角形
2、有两个角的和是90°的三角形是直角三角形;
一、判断题. 1. ABC的两边AB=5,AC=12,则BC=13 ( )
2. ABC的a=6,b=8,则c=10 ( )
巩固练习:
二、选择题
1.满足下列条件△ABC,不是直角三角形的是( )
A.b2=a2-c2 B. a:b:c=3:4:5
C.∠C=∠A-∠B D.∠A:∠B :∠C =3:4:5
D
2.下列各组线段中,能组成直角三角形的是( )
A. 5,6,7 B. 32,42,52
C. 5,11,12 D. 5,12,13
D
巩固练习:
3.三角形三边长a、b、c满足条件
则此三角形是( )
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等边三角形
B
1、已知:在△ABC中, AB=15cm,AC=20cm,
BC=25cm,AD是BC边上的高。求: AD的长。
作业:
一:课堂作业
