15.3中心对称课件
图片预览





文档简介
(共27张PPT)
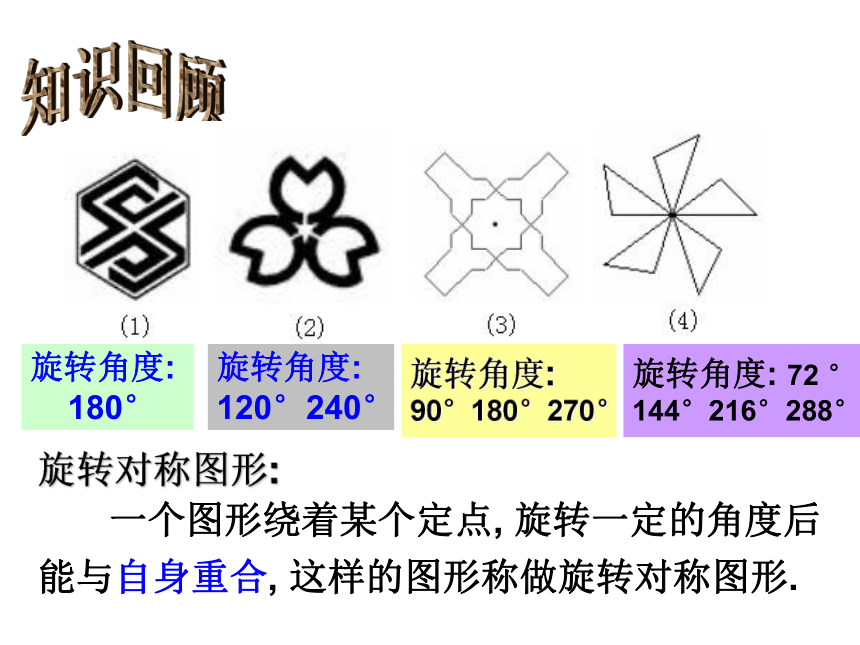
旋转对称图形:
一个图形绕着某个定点, 旋转一定的角度后
能与自身重合, 这样的图形称做旋转对称图形.
旋转角度:
120°240°
旋转角度:
180°
旋转角度:
90°180°270°
旋转角度: 72 °
144°216°288°
(1) 这些图形有什么共同的特征?
(2)这些图形都可以绕某个点旋转哪个角度后与原来的图形重合
在平面内,一个图形绕某个点旋转180o,如果旋转前后的图形互相重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心
注意:中心对称图形是 旋转角度为180度的 旋转对称图形.
中心对称图形和旋转对称图形的关系
中心对称图形是特殊的旋转对称图形,因此中心对称图形都属于旋转对称图形,但旋转对称图形不一定是中心对称图形(如图).
1、小明说:我发现正三角形绕着中心旋转某一个角度,旋转前后的图形互相重合,所以三角形是中心对称图形。你同意吗?
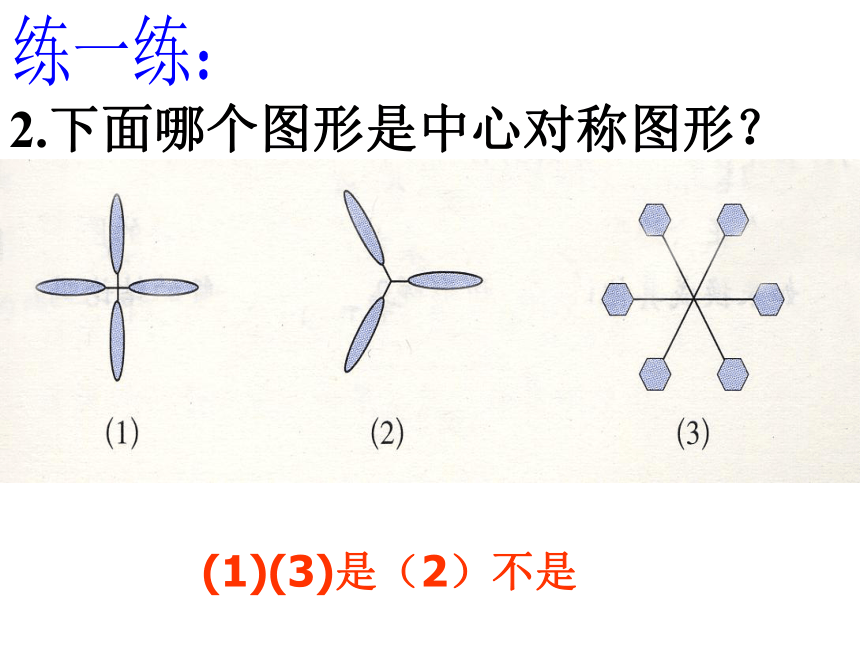
2.下面哪个图形是中心对称图形?
(1)(3)是(2)不是
3、下列图形哪些是轴对称图形,哪些是中心对称图形?
(1)平行四边形 (2)矩形
(3)正方形 (4)等腰梯形
(5)等边三角形
A
C
B
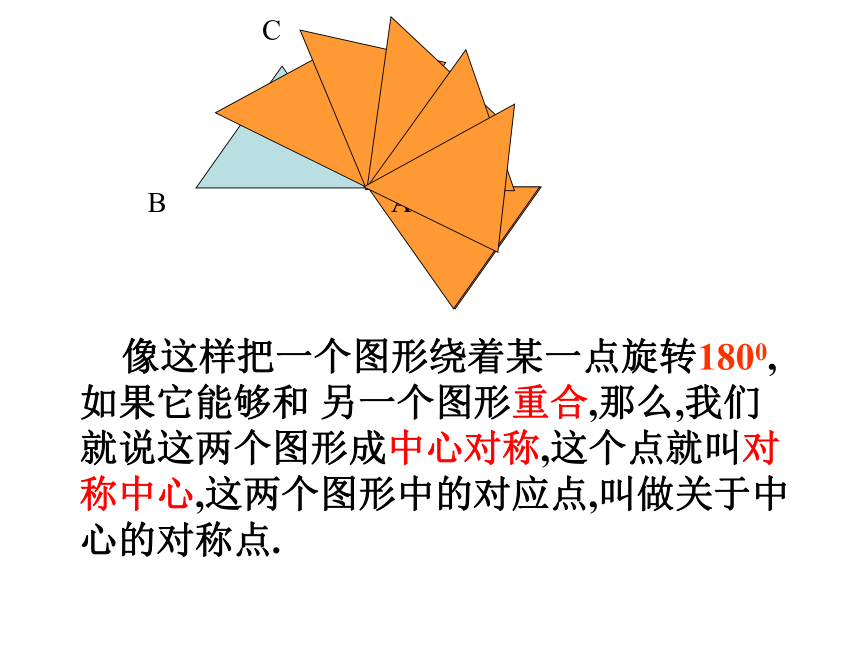
像这样把一个图形绕着某一点旋转1800,如果它能够和 另一个图形重合,那么,我们就说这两个图形成中心对称,这个点就叫对称中心,这两个图形中的对应点,叫做关于中心的对称点.
A
B
C
D
E
F
O
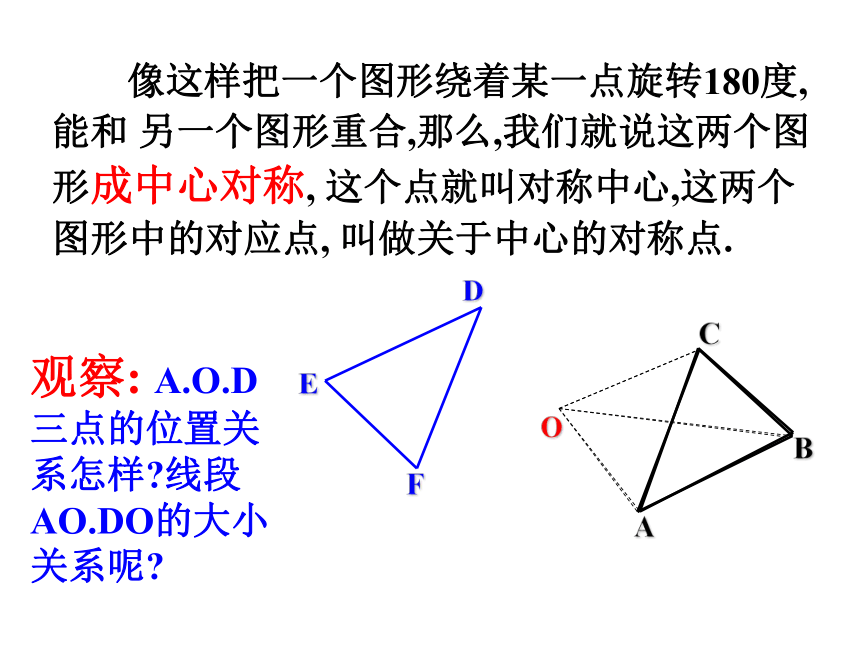
像这样把一个图形绕着某一点旋转180度, 能和 另一个图形重合,那么,我们就说这两个图形成中心对称, 这个点就叫对称中心,这两个图形中的对应点, 叫做关于中心的对称点.
观察: A.O.D三点的位置关系怎样 线段AO.DO的大小关系呢
A
B
C
O
D
E
F
由旋转180°知道A、O、D三点在一直线上,
B、O、E
且OA=OD,
同理 在一直线上,
且 ,
C、O、F
在一直线上, 且
OC=OF.
OB=OE
个图形中, 连结
即:成中心对称的两
对应点的线段都
经过对称中心, 且被对称中心所平分.
反过来,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.
例1: 如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O。
A
B
C
A’
B’
C’
解法一:根据观察,B、B’应是对应点,连结BB’,用刻度尺找出BB’的中点O,则点O即为所求(如图)
A
B
C
A’
B’
C’
O
O
解法二:根据观察,B、B’及C、C’应是两组对应点,连结BB’、CC’,BB’、CC’相交于点O,则点O即为所求(如图)。
A
B
C
A’
B’
C’
例2、 如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称。
·
O
A
B
C
D
E
F
解:
(1)连接AO并延长AO到D,使OD=OA,于是得到点A的对称点D。
(2)同样画出点B和点C的对称点E和F;
(3)顺次连接DE、、FD、EF。
△DEF即为所求的三角形
A
B
B′
A′
A
B
C
D
E
F
⑴如图, 线段AB和线段AB关于某一点成中心对
称, 试找出它们的对称中心.
O
·
′
′
⑵如图△ABC和△FED是成中心对
称的两个三角形,试找出对称中心.
画法:连结对应点C、D和B、E,
·
O
CD与BE相交于点O,则点O就是所要找
的对称中心。
∥
∥
∥
∥
∥
∥
(3)已知四边形ABCD和点O画四边形
A′B′C′D′,使它与已知四边形关于点O对称。
A
B
C
D
O
A`
.
D`
.
C`
.
B`
.
A
B
C
C
1
A
1
B
1
O
轴对称 中心对称
有一条对称轴---直线 有一个对称中心---点
图形沿对称轴对折(翻折1800)后重合 图形绕对称中心旋转1800后重合
对称点的连线被对称轴垂直平分 对称点连线经过对称中心,且被对称中心平分
中心对称与轴对称有什么区别与联系
翻转或旋转前后的图形的大小、形状不变。
如图,等边△ABC及其中心O,画△DEF,
使△DEF和△ABC关于点O成中心对称.
O
·
D
A
B
C
E
F
⑴连结AO, 并延长到D,
解:
点D就是点A关于点O的对称点
使OD=OA,
⑵同理画出点B、C关于点O
的对称点
⑶顺次连结DE、EF、FD
则△DEF就是所求作的三角形.
B2
例3
如图,已知△ABC和一点P,
⑴画△ABC关于点P的对称图形△A1B1C1;
⑵过点P任意画一条直线m,画△ABC关于直
线m的对称图形△A2B2C2;
·
P
A
B
C
A1
B1
C1
A2
C2
m
观察△A1B1C1 和△ A2B2C2
它们有什么关系吗
n
已知四边形ABCD关于点P成中心对称的四
边形EFGH,, 试画出四边形EFGH.
P
·
A
B
C
D
·
E
F
G
H
例3
请以给定的图形○○△△=(两个圆,两个三角形,两条平行线)为构件,尽可能多地构思有意义的一些中心图形,并写上一两句贴切,诙谐的解说词.如下图就是符合要求的图形,你能构思其它图形吗 比一比,看谁想得多,看谁想得妙!
想 一 想
路灯与倒影
指南针
除号
沙漏
两只拔河的小鸡
想 一 想
例4:图中有一个圆和一个矩形,你能否只画一直线就将两个图形分成形状、大小都相同的两部分。
如图中, 试画一条直线, 把该图形分成两部
分, 且使两部分面积相等.
分割法
补方法
例5
1、确定对称中心
2、画中心对称图形
今天你学到了什么
方法1:一组对称点连线段的中点.
方法2:两组对称点连线的交点.
⑴若无对称中心,应先确定对称中心;
⑵用已知图形上的点与对称中心连线段,并延
长加倍画出中心对称点;
⑶顺次连结对应线段,得到中习对称图形.
旋转对称图形:
一个图形绕着某个定点, 旋转一定的角度后
能与自身重合, 这样的图形称做旋转对称图形.
旋转角度:
120°240°
旋转角度:
180°
旋转角度:
90°180°270°
旋转角度: 72 °
144°216°288°
(1) 这些图形有什么共同的特征?
(2)这些图形都可以绕某个点旋转哪个角度后与原来的图形重合
在平面内,一个图形绕某个点旋转180o,如果旋转前后的图形互相重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心
注意:中心对称图形是 旋转角度为180度的 旋转对称图形.
中心对称图形和旋转对称图形的关系
中心对称图形是特殊的旋转对称图形,因此中心对称图形都属于旋转对称图形,但旋转对称图形不一定是中心对称图形(如图).
1、小明说:我发现正三角形绕着中心旋转某一个角度,旋转前后的图形互相重合,所以三角形是中心对称图形。你同意吗?
2.下面哪个图形是中心对称图形?
(1)(3)是(2)不是
3、下列图形哪些是轴对称图形,哪些是中心对称图形?
(1)平行四边形 (2)矩形
(3)正方形 (4)等腰梯形
(5)等边三角形
A
C
B
像这样把一个图形绕着某一点旋转1800,如果它能够和 另一个图形重合,那么,我们就说这两个图形成中心对称,这个点就叫对称中心,这两个图形中的对应点,叫做关于中心的对称点.
A
B
C
D
E
F
O
像这样把一个图形绕着某一点旋转180度, 能和 另一个图形重合,那么,我们就说这两个图形成中心对称, 这个点就叫对称中心,这两个图形中的对应点, 叫做关于中心的对称点.
观察: A.O.D三点的位置关系怎样 线段AO.DO的大小关系呢
A
B
C
O
D
E
F
由旋转180°知道A、O、D三点在一直线上,
B、O、E
且OA=OD,
同理 在一直线上,
且 ,
C、O、F
在一直线上, 且
OC=OF.
OB=OE
个图形中, 连结
即:成中心对称的两
对应点的线段都
经过对称中心, 且被对称中心所平分.
反过来,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.
例1: 如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O。
A
B
C
A’
B’
C’
解法一:根据观察,B、B’应是对应点,连结BB’,用刻度尺找出BB’的中点O,则点O即为所求(如图)
A
B
C
A’
B’
C’
O
O
解法二:根据观察,B、B’及C、C’应是两组对应点,连结BB’、CC’,BB’、CC’相交于点O,则点O即为所求(如图)。
A
B
C
A’
B’
C’
例2、 如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称。
·
O
A
B
C
D
E
F
解:
(1)连接AO并延长AO到D,使OD=OA,于是得到点A的对称点D。
(2)同样画出点B和点C的对称点E和F;
(3)顺次连接DE、、FD、EF。
△DEF即为所求的三角形
A
B
B′
A′
A
B
C
D
E
F
⑴如图, 线段AB和线段AB关于某一点成中心对
称, 试找出它们的对称中心.
O
·
′
′
⑵如图△ABC和△FED是成中心对
称的两个三角形,试找出对称中心.
画法:连结对应点C、D和B、E,
·
O
CD与BE相交于点O,则点O就是所要找
的对称中心。
∥
∥
∥
∥
∥
∥
(3)已知四边形ABCD和点O画四边形
A′B′C′D′,使它与已知四边形关于点O对称。
A
B
C
D
O
A`
.
D`
.
C`
.
B`
.
A
B
C
C
1
A
1
B
1
O
轴对称 中心对称
有一条对称轴---直线 有一个对称中心---点
图形沿对称轴对折(翻折1800)后重合 图形绕对称中心旋转1800后重合
对称点的连线被对称轴垂直平分 对称点连线经过对称中心,且被对称中心平分
中心对称与轴对称有什么区别与联系
翻转或旋转前后的图形的大小、形状不变。
如图,等边△ABC及其中心O,画△DEF,
使△DEF和△ABC关于点O成中心对称.
O
·
D
A
B
C
E
F
⑴连结AO, 并延长到D,
解:
点D就是点A关于点O的对称点
使OD=OA,
⑵同理画出点B、C关于点O
的对称点
⑶顺次连结DE、EF、FD
则△DEF就是所求作的三角形.
B2
例3
如图,已知△ABC和一点P,
⑴画△ABC关于点P的对称图形△A1B1C1;
⑵过点P任意画一条直线m,画△ABC关于直
线m的对称图形△A2B2C2;
·
P
A
B
C
A1
B1
C1
A2
C2
m
观察△A1B1C1 和△ A2B2C2
它们有什么关系吗
n
已知四边形ABCD关于点P成中心对称的四
边形EFGH,, 试画出四边形EFGH.
P
·
A
B
C
D
·
E
F
G
H
例3
请以给定的图形○○△△=(两个圆,两个三角形,两条平行线)为构件,尽可能多地构思有意义的一些中心图形,并写上一两句贴切,诙谐的解说词.如下图就是符合要求的图形,你能构思其它图形吗 比一比,看谁想得多,看谁想得妙!
想 一 想
路灯与倒影
指南针
除号
沙漏
两只拔河的小鸡
想 一 想
例4:图中有一个圆和一个矩形,你能否只画一直线就将两个图形分成形状、大小都相同的两部分。
如图中, 试画一条直线, 把该图形分成两部
分, 且使两部分面积相等.
分割法
补方法
例5
1、确定对称中心
2、画中心对称图形
今天你学到了什么
方法1:一组对称点连线段的中点.
方法2:两组对称点连线的交点.
⑴若无对称中心,应先确定对称中心;
⑵用已知图形上的点与对称中心连线段,并延
长加倍画出中心对称点;
⑶顺次连结对应线段,得到中习对称图形.
