六年级下册数学课件-3.1比例意义、基本性质和解比例 青岛版(共22张PPT)
文档属性
| 名称 | 六年级下册数学课件-3.1比例意义、基本性质和解比例 青岛版(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 944.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 14:54:22 | ||
图片预览







文档简介
三 啤酒生产中的数学
— 比例
3.1 比例的意义、基本性质
和解比例
回顾复习
1.求下列圆柱的体积。
2.求下列圆锥的体积。
×5.6×3
1
3
(1) S=5.6dm2 h=3dm
(2) r=6cm h=20cm
= 5.6(dm3)
×3.14×62×20
1
3
= ×3.14×36×20
1
3
= 753.6(cm3)
从图中,你知道了哪些数学信息?
运动会报名
男生志愿者
王东 李明 刘刚
李亮 丁一 张帅
于军 刘平 赵海
女生志愿者
李燕 王静 牛莉
方悦 于美 张红
孙娟
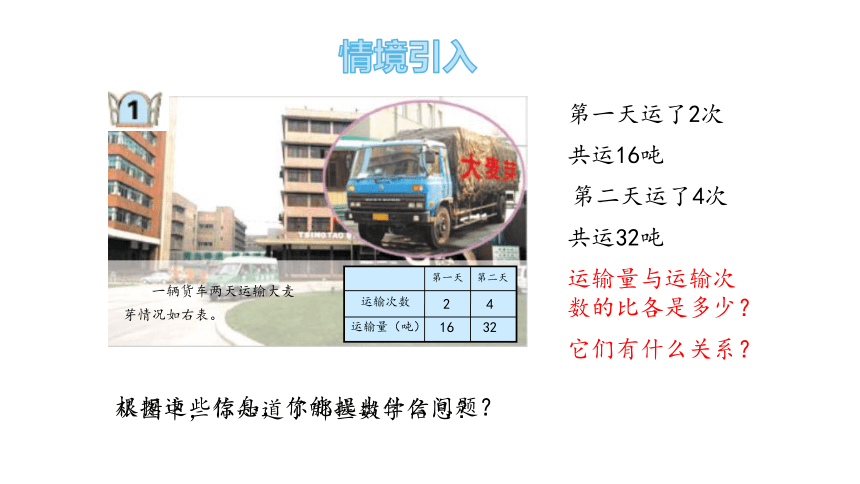
第一天运了2次
共运16吨
共运32吨
根据这些信息,你能提出什么问题?
运输量与运输次数的比各是多少?
一辆货车两天运输大麦
芽情况如右表。
运输次数
运输量(吨)
第一天
第二天
2 4
16 32
第二天运了4次
它们有什么关系?
情境引入
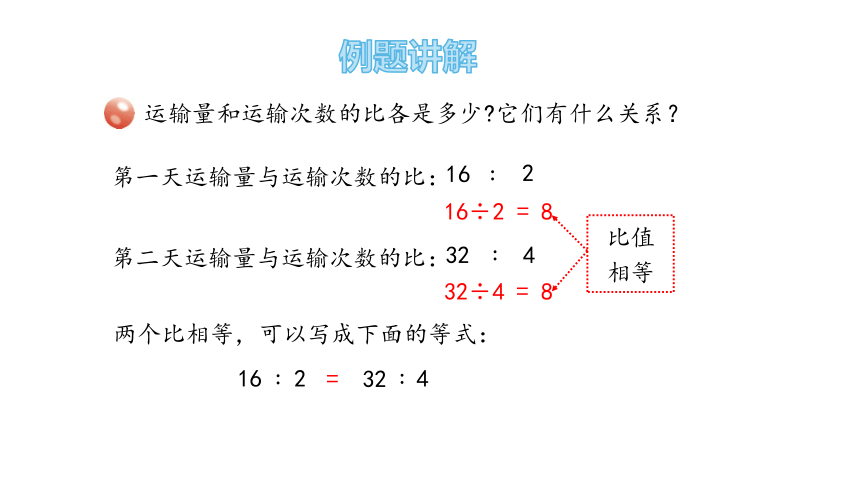
运输量和运输次数的比各是多少?它们有什么关系?
16
2
32
4
:
第一天运输量与运输次数的比:
第二天运输量与运输次数的比:
:
16÷2 = 8
32÷4 = 8
比值
相等
16
2
32
4
:
:
=
两个比相等,可以写成下面的等式:
例题讲解
表示两个比相等的式子叫作比例。组成比例的四个数叫作比例的项。两端的两项叫作比例的外项,中间的两项叫作比例的内项。
16
2
32
4
:
:
=
内项
外项
也可以写成
16
2
32
4
16
2
32
4
:
:
=
=
内项
外项
18:3=30:5
18:30=3:5
3:18=5:30
30:18=5:3
运输次数
运输量(吨)
第一天
第二天
3 5
18 30
你能写出哪些比例?
在比例里,两个外项与两个内项之间有什么关系呢?
可以以“18:3=30:5”为例来研究,也可以自己举例来研究。
分别算出两个外项和两个内项的和、差、积、商,看看从中能发现什么规律?
两个外项的和与两个内项的和:
两个外项的和:18 + 5 = 23
两个内项的和:3 + 30 = 33
两个外项的和与两个内项的和之间没有发现规律。
18 : 3 = 30 : 5
两个外项的差与两个内项的差:
两个外项的差:18 - 5 = 13
两个内项的差:30 - 3 = 27
18 : 3 = 30 : 5
两个外项的和与两个内项的和之间没有发现规律。
两个外项的积与两个内项的积:
两个外项的积:18 × 5 = 90
两个内项的和:3 × 30 = 90
18 : 3 = 30 : 5
两个外项的积等于两个内项的积。
两个外项的商与两个内项的商:
两个外项的商:18 ÷ 5 = 3.6
两个内项的商:30÷ 3 = 10
1 8 : 3 = 30 : 5
两个外项的商与两个内项的商之间没有发现规律。
回顾刚才的研究,可以得出一个什么结论?
在比例里,两个外项的积等于两个内项的积。
这是不是一个规律呢?我们来验证一下。
两个内项的积:4 ×100 = 400
两个外项的积:80 × 5 = 400
=
40 : 2 = 60 : 3
两个内项的积:2 × 60 = 120
两个外项的积:40 × 3 = 120
举例验证:
10 : 7 = 20 :14
两个内项的积:7 × 20 = 140
两个外项的积:10 ×14 = 140
…
在比例里,两个外项的积等于两个内项的积。这叫作比例的基本性质。
你能求出下面比例中的未知项吗?
20 : 25 = 4 : x
解: 20x = 25 × 4
20x = 100
x = 5
求比例中的未知项,叫作解比例。
小 结
比例的意义、基本性质和解比例
1.比例的相关概念
表示两个比相等的式子叫作比例。组成比例的四个数,叫作比例的项。两端的两项叫做比例的外项,中间的两项叫作比例的内项。
2.比例的基本性质
在比例里,两个外项的积等于两个内项的积。
3.解比例
求比例中的未知项,叫作解比例。
培优例题
例1 用2、3.6、4.5和x组成比例x的值是多少?
不要遗漏哦!
规范解答:
当x和2同为内项(或外项),则2x=3.6×4.5所以x=8.1
当x和3.6同为内项(或外项),则3.6x=2×4.5所以x=2.5
当x和4.5同为内项(或外项),则4.5x=3.6×2所以x=1.6
例2 用食盐水浸泡菠萝,可以使菠萝的口感变甜,能降低菠萝中草酸与菠萝酶的含量,还能预防菠萝过敏。 食盐与水的比是 2 ∶ 83, 配制 340 克食盐水,需要多少克食盐?
规范解答:
解:设需要 x 克食盐。已知食盐与水的比是 2 ∶ 83,所以食盐与食盐水的比为 2 ∶(2+83)
2 ∶(2+83)=x ∶ 340
85x=680
x=8
答:需要 8 克食盐。
(2)后4天加工的数量和所用时间的比是______。
(1)前3天加工的数量和所用时间的比是______。
(3)这两个比能组成比例吗?为什么?
150:3
200:4
150 : 3 = 200 : 4
150 ÷ 3 = 50
200 ÷ 4 = 50
后4天加工
了200个。
前3天加工
了150个,
随堂小测
1.
能组成比例,因为两个比对应的比值相等
2.声音在空气中的传播情况如下表。
时间(秒)
1
2
3
4
…
10
距离(米)
340
680
1020
1360
…
3400
=340
340
1
=340
1020
3
=340
680
2
=340
1360
4
(1)写出相对应的距离与时间的比,求出比值并比较大小。
所有比值都相等。
(2)说说这个比值所表示的意义。
这个比值表示声音在空气中的传播速度。
(3)表中的数据能组成比例吗?请写出几个。
340
1
680
2
1020
3
1360
4
=
=
2
3.下列4个数能组成比例吗?请把组成的比例写下来。
怎样判断比较简单?
20
30
2:3=20:30
你是怎么判断的?
3
2:20=3:30
30:3=20:2
3:2=30:20
20:30=2:3
3:30=2:20
20:2=30:3
30:20=3:2
5
0.4
0.3
6
6×0.3 ≠0.4×5
怎样改就组成比例了?
=
=
4.解比例。
=
2︰
解:4x = 5×9
4x = 45
解:2x =
2x =
x =
×
45
4
3
5
2
3
2
5
1
5
x =
— 比例
3.1 比例的意义、基本性质
和解比例
回顾复习
1.求下列圆柱的体积。
2.求下列圆锥的体积。
×5.6×3
1
3
(1) S=5.6dm2 h=3dm
(2) r=6cm h=20cm
= 5.6(dm3)
×3.14×62×20
1
3
= ×3.14×36×20
1
3
= 753.6(cm3)
从图中,你知道了哪些数学信息?
运动会报名
男生志愿者
王东 李明 刘刚
李亮 丁一 张帅
于军 刘平 赵海
女生志愿者
李燕 王静 牛莉
方悦 于美 张红
孙娟
第一天运了2次
共运16吨
共运32吨
根据这些信息,你能提出什么问题?
运输量与运输次数的比各是多少?
一辆货车两天运输大麦
芽情况如右表。
运输次数
运输量(吨)
第一天
第二天
2 4
16 32
第二天运了4次
它们有什么关系?
情境引入
运输量和运输次数的比各是多少?它们有什么关系?
16
2
32
4
:
第一天运输量与运输次数的比:
第二天运输量与运输次数的比:
:
16÷2 = 8
32÷4 = 8
比值
相等
16
2
32
4
:
:
=
两个比相等,可以写成下面的等式:
例题讲解
表示两个比相等的式子叫作比例。组成比例的四个数叫作比例的项。两端的两项叫作比例的外项,中间的两项叫作比例的内项。
16
2
32
4
:
:
=
内项
外项
也可以写成
16
2
32
4
16
2
32
4
:
:
=
=
内项
外项
18:3=30:5
18:30=3:5
3:18=5:30
30:18=5:3
运输次数
运输量(吨)
第一天
第二天
3 5
18 30
你能写出哪些比例?
在比例里,两个外项与两个内项之间有什么关系呢?
可以以“18:3=30:5”为例来研究,也可以自己举例来研究。
分别算出两个外项和两个内项的和、差、积、商,看看从中能发现什么规律?
两个外项的和与两个内项的和:
两个外项的和:18 + 5 = 23
两个内项的和:3 + 30 = 33
两个外项的和与两个内项的和之间没有发现规律。
18 : 3 = 30 : 5
两个外项的差与两个内项的差:
两个外项的差:18 - 5 = 13
两个内项的差:30 - 3 = 27
18 : 3 = 30 : 5
两个外项的和与两个内项的和之间没有发现规律。
两个外项的积与两个内项的积:
两个外项的积:18 × 5 = 90
两个内项的和:3 × 30 = 90
18 : 3 = 30 : 5
两个外项的积等于两个内项的积。
两个外项的商与两个内项的商:
两个外项的商:18 ÷ 5 = 3.6
两个内项的商:30÷ 3 = 10
1 8 : 3 = 30 : 5
两个外项的商与两个内项的商之间没有发现规律。
回顾刚才的研究,可以得出一个什么结论?
在比例里,两个外项的积等于两个内项的积。
这是不是一个规律呢?我们来验证一下。
两个内项的积:4 ×100 = 400
两个外项的积:80 × 5 = 400
=
40 : 2 = 60 : 3
两个内项的积:2 × 60 = 120
两个外项的积:40 × 3 = 120
举例验证:
10 : 7 = 20 :14
两个内项的积:7 × 20 = 140
两个外项的积:10 ×14 = 140
…
在比例里,两个外项的积等于两个内项的积。这叫作比例的基本性质。
你能求出下面比例中的未知项吗?
20 : 25 = 4 : x
解: 20x = 25 × 4
20x = 100
x = 5
求比例中的未知项,叫作解比例。
小 结
比例的意义、基本性质和解比例
1.比例的相关概念
表示两个比相等的式子叫作比例。组成比例的四个数,叫作比例的项。两端的两项叫做比例的外项,中间的两项叫作比例的内项。
2.比例的基本性质
在比例里,两个外项的积等于两个内项的积。
3.解比例
求比例中的未知项,叫作解比例。
培优例题
例1 用2、3.6、4.5和x组成比例x的值是多少?
不要遗漏哦!
规范解答:
当x和2同为内项(或外项),则2x=3.6×4.5所以x=8.1
当x和3.6同为内项(或外项),则3.6x=2×4.5所以x=2.5
当x和4.5同为内项(或外项),则4.5x=3.6×2所以x=1.6
例2 用食盐水浸泡菠萝,可以使菠萝的口感变甜,能降低菠萝中草酸与菠萝酶的含量,还能预防菠萝过敏。 食盐与水的比是 2 ∶ 83, 配制 340 克食盐水,需要多少克食盐?
规范解答:
解:设需要 x 克食盐。已知食盐与水的比是 2 ∶ 83,所以食盐与食盐水的比为 2 ∶(2+83)
2 ∶(2+83)=x ∶ 340
85x=680
x=8
答:需要 8 克食盐。
(2)后4天加工的数量和所用时间的比是______。
(1)前3天加工的数量和所用时间的比是______。
(3)这两个比能组成比例吗?为什么?
150:3
200:4
150 : 3 = 200 : 4
150 ÷ 3 = 50
200 ÷ 4 = 50
后4天加工
了200个。
前3天加工
了150个,
随堂小测
1.
能组成比例,因为两个比对应的比值相等
2.声音在空气中的传播情况如下表。
时间(秒)
1
2
3
4
…
10
距离(米)
340
680
1020
1360
…
3400
=340
340
1
=340
1020
3
=340
680
2
=340
1360
4
(1)写出相对应的距离与时间的比,求出比值并比较大小。
所有比值都相等。
(2)说说这个比值所表示的意义。
这个比值表示声音在空气中的传播速度。
(3)表中的数据能组成比例吗?请写出几个。
340
1
680
2
1020
3
1360
4
=
=
2
3.下列4个数能组成比例吗?请把组成的比例写下来。
怎样判断比较简单?
20
30
2:3=20:30
你是怎么判断的?
3
2:20=3:30
30:3=20:2
3:2=30:20
20:30=2:3
3:30=2:20
20:2=30:3
30:20=3:2
5
0.4
0.3
6
6×0.3 ≠0.4×5
怎样改就组成比例了?
=
=
4.解比例。
=
2︰
解:4x = 5×9
4x = 45
解:2x =
2x =
x =
×
45
4
3
5
2
3
2
5
1
5
x =
