(试题4)28.1锐角三角函数
文档属性
| 名称 | (试题4)28.1锐角三角函数 |  | |
| 格式 | zip | ||
| 文件大小 | 82.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-01 21:32:17 | ||
图片预览
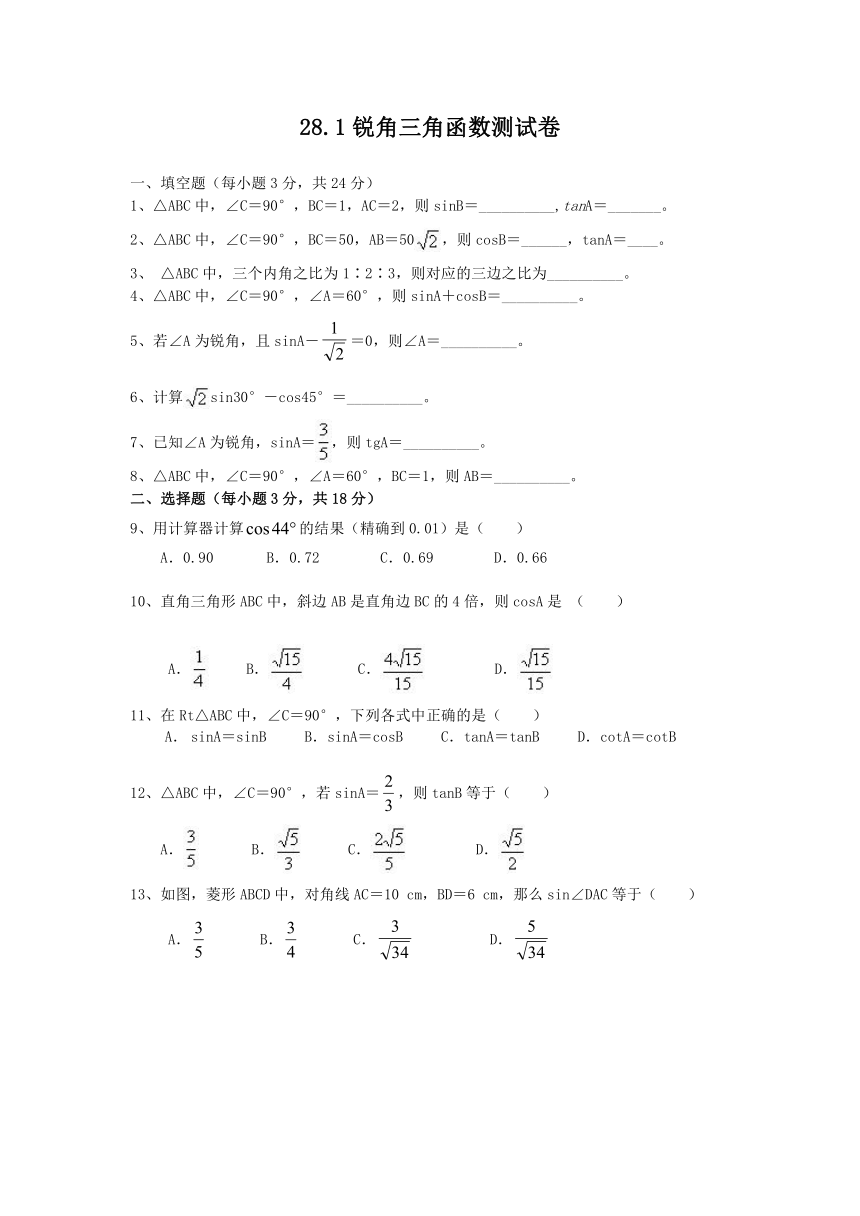


文档简介
28.1锐角三角函数测试卷
一、填空题(每小题3分,共24分)
1、△ABC中,∠C=90°,BC=1,AC=2,则sinB=__________,tanA=_______。
2、△ABC中,∠C=90°,BC=50,AB=50,则cosB=______,tanA=____。
3、 △ABC中,三个内角之比为1∶2∶3,则对应的三边之比为__________。
4、△ABC中,∠C=90°,∠A=60°,则sinA+cosB=__________。
5、若∠A为锐角,且sinA-=0,则∠A=__________。
6、计算sin30°-cos45°=__________。
7、已知∠A为锐角,sinA=,则tgA=__________。
8、△ABC中,∠C=90°,∠A=60°,BC=1,则AB=__________。
二、选择题(每小题3分,共18分)
9、用计算器计算的结果(精确到0.01)是( )
A.0.90 B.0.72 C.0.69 D.0.66
10、直角三角形ABC中,斜边AB是直角边BC的4倍,则cosA是 ( )
A. B. HYPERLINK "http://www./Index.html" C. D.
11、在Rt△ABC中,∠C=90°,下列各式中正确的是( )
sinA=sinB B.sinA=cosB C.tanA=tanB D.cotA=cotB
12、△ABC中,∠C=90°,若sinA=,则tanB等于( )
A. B. C. D.
13、如图,菱形ABCD中,对角线AC=10 cm,BD=6 cm,那么sin∠DAC等于( )
A. B. C. D.
( http: / / www. / Index.html )
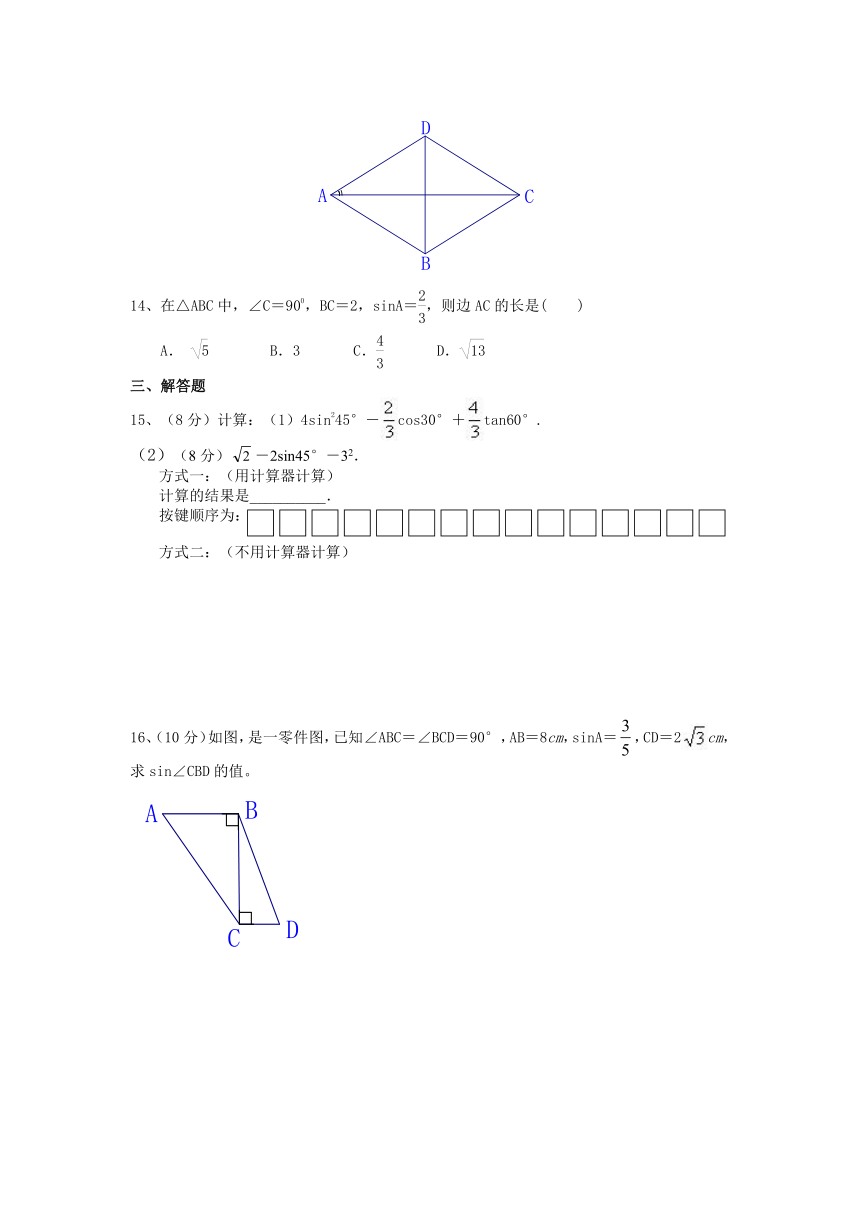
14、在△ABC中,∠C=900,BC=2,sinA=,则边AC的长是( )
A. B.3 C. D.
三、解答题
15、(8分)计算:(1)4sin245°-cos30°+tan60°.
(2)(8分)-2sin45°-32.
方式一:(用计算器计算)
计算的结果是__________.
按键顺序为:
方式二:(不用计算器计算)
16、(10分)如图,是一零件图,已知∠ABC=∠BCD=90°,AB=8cm,sinA=,CD=2cm,求sin∠CBD的值。
17、(本题10分)如图,△ABC是一仓库的屋顶的截面图,若∠B=30°,∠C=45°,AC=2,求线段AB长。
18、(本题10分)求tan15°的值.(提示:先画一30°角的Rt△ABC,∠A=30°,延长CA到D,使AD=AB,构造出15°的锐角,求解)
19、(本题12分)如图,在平面直角坐标系中,点A在第一象限,点B的坐标为(3,0),OA=2,∠AOB=60°.
(1)求点A的坐标;
(2)若直线AB交x轴于点C,求△AOC的面积。
参考答案:
填空题
1、,;2、,1;3、1∶∶2;4、;5、45°;6、0; 7、;8、;
二、选择题
9、B; 10、B;11、B;12、D;13、C;14、A ;
三、
15、(1)解:原式=4×-+
=2-+=2+;
(2)方式一:(用计算器计算)
计算的结果是 -9 .
按键顺序为:
方式二:(不用计算器计算)
原式=-2×-9
=--9
=-9
16、解:由 sinA==, 设BC=3,AC=5,
则根据勾股定理,得 AB==4;
∵ AB=8 cm, ∴ =2,
∴ BC=6 cm,
在Rt△BCD中,BD===4 cm;
∴ sin∠CBD===;
17、解:过A作AD⊥BC,
在Rt△ADC中,∵ ∠C=45°,
∴ sinC==,
∴ AD=,
在Rt△ABD中,∵ ∠B=30°,
∴ sinB==,
∴ AB=2AD=2.
18、解:延长CA到D,使AD=AB,则∠D=∠ABD,
∵∠BAC=30°,∴∠D=15°;设BC=1,则AB=2,AC=,
∴ tan15°== HYPERLINK "http://www./Index.html" ===2-.
19、解:(1)过点A作AD⊥x轴,垂足为D
则OD=OA cos60°=2×=1,
AD=OA sin60°=2×=,
∴点A的坐标为(1,)
(2)设直线AB的解析式为y=kx+b,
则有
∴直线AB的解析式为y
令x=0,得,∴
备选题
一、填空题
1、sin53°cos37°+cos53°sin37°= .
2、如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径,,则的值是_____。
( http: / / www. / Index.html )
二、选择题
3、在△ABC中,∠C = 90°,∠B=50°,AB=10,则BC的长为( )
A.10tan50° B.10cos20° C.10sin50° D.
4、如图所示,AB是⊙O的直径,弦AC、BD相交于E,则等于( )
A、 B、
C、 D、
三、计算解答题
5、cos21°+cos22°+···+cos288°+cos289°.
6、如图,在梯形ABCD中,AB∥CD,∠BCD=90°,且AB=1,BC=2,tan∠ADC=2.
求证:DC=BC;
E是梯形内一点,F是梯形外一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论;
在(2)的条件下,当BE:CE=1:2,∠BEC=135°时,求sin∠BFE的值.
7、(本题12分)已知:⊙O的半径是8,直线PA,PB为⊙O的切线,A、B两点为点,
(1)当OP为何值时,∠APB=90°.
(2)若∠APB=50°,求AP的长度(结果保留三位有效数字).
(参考数据sin50°=O.7660,cos50°=0.6428,tan50°=1.1918,sin25°=0.4226,cos25°=0.9063,tan25°=O.4663)
参考答案:
1、1;2、.3、B.4、D;
5、原式=44.5
6、(1)过A作DC的垂线AM交DC于M,
则AM=BC=2.
又tan∠ADC=2,所以 HYPERLINK "http://www./Index.html" .即DC=BC.
(2)等腰三角形.
证明:因为.
所以,△DEC≌△BFC
所以,.
所以,
即△ECF是等腰直角三角形.
(3)设,则,所以.
因为,又,所以.
所以
所以.
7、(1)解:连结OA
∵PA,PB是⊙O的切线
∴∠PAO=90°,∠APO=∠BPO
∵∠APB=90°
∴∠APO=45°
∴∠AOP=45°
∴OA=PA=8
∴OP=
(2)解:连结OA
∵PA,PB是⊙O的切线
∴∠APO=∠BPO=∠APB=25°
∵ HYPERLINK "http://www./Index.html"
∴
A
B
C
C
D
B
A
O
E
一、填空题(每小题3分,共24分)
1、△ABC中,∠C=90°,BC=1,AC=2,则sinB=__________,tanA=_______。
2、△ABC中,∠C=90°,BC=50,AB=50,则cosB=______,tanA=____。
3、 △ABC中,三个内角之比为1∶2∶3,则对应的三边之比为__________。
4、△ABC中,∠C=90°,∠A=60°,则sinA+cosB=__________。
5、若∠A为锐角,且sinA-=0,则∠A=__________。
6、计算sin30°-cos45°=__________。
7、已知∠A为锐角,sinA=,则tgA=__________。
8、△ABC中,∠C=90°,∠A=60°,BC=1,则AB=__________。
二、选择题(每小题3分,共18分)
9、用计算器计算的结果(精确到0.01)是( )
A.0.90 B.0.72 C.0.69 D.0.66
10、直角三角形ABC中,斜边AB是直角边BC的4倍,则cosA是 ( )
A. B. HYPERLINK "http://www./Index.html" C. D.
11、在Rt△ABC中,∠C=90°,下列各式中正确的是( )
sinA=sinB B.sinA=cosB C.tanA=tanB D.cotA=cotB
12、△ABC中,∠C=90°,若sinA=,则tanB等于( )
A. B. C. D.
13、如图,菱形ABCD中,对角线AC=10 cm,BD=6 cm,那么sin∠DAC等于( )
A. B. C. D.
( http: / / www. / Index.html )
14、在△ABC中,∠C=900,BC=2,sinA=,则边AC的长是( )
A. B.3 C. D.
三、解答题
15、(8分)计算:(1)4sin245°-cos30°+tan60°.
(2)(8分)-2sin45°-32.
方式一:(用计算器计算)
计算的结果是__________.
按键顺序为:
方式二:(不用计算器计算)
16、(10分)如图,是一零件图,已知∠ABC=∠BCD=90°,AB=8cm,sinA=,CD=2cm,求sin∠CBD的值。
17、(本题10分)如图,△ABC是一仓库的屋顶的截面图,若∠B=30°,∠C=45°,AC=2,求线段AB长。
18、(本题10分)求tan15°的值.(提示:先画一30°角的Rt△ABC,∠A=30°,延长CA到D,使AD=AB,构造出15°的锐角,求解)
19、(本题12分)如图,在平面直角坐标系中,点A在第一象限,点B的坐标为(3,0),OA=2,∠AOB=60°.
(1)求点A的坐标;
(2)若直线AB交x轴于点C,求△AOC的面积。
参考答案:
填空题
1、,;2、,1;3、1∶∶2;4、;5、45°;6、0; 7、;8、;
二、选择题
9、B; 10、B;11、B;12、D;13、C;14、A ;
三、
15、(1)解:原式=4×-+
=2-+=2+;
(2)方式一:(用计算器计算)
计算的结果是 -9 .
按键顺序为:
方式二:(不用计算器计算)
原式=-2×-9
=--9
=-9
16、解:由 sinA==, 设BC=3,AC=5,
则根据勾股定理,得 AB==4;
∵ AB=8 cm, ∴ =2,
∴ BC=6 cm,
在Rt△BCD中,BD===4 cm;
∴ sin∠CBD===;
17、解:过A作AD⊥BC,
在Rt△ADC中,∵ ∠C=45°,
∴ sinC==,
∴ AD=,
在Rt△ABD中,∵ ∠B=30°,
∴ sinB==,
∴ AB=2AD=2.
18、解:延长CA到D,使AD=AB,则∠D=∠ABD,
∵∠BAC=30°,∴∠D=15°;设BC=1,则AB=2,AC=,
∴ tan15°== HYPERLINK "http://www./Index.html" ===2-.
19、解:(1)过点A作AD⊥x轴,垂足为D
则OD=OA cos60°=2×=1,
AD=OA sin60°=2×=,
∴点A的坐标为(1,)
(2)设直线AB的解析式为y=kx+b,
则有
∴直线AB的解析式为y
令x=0,得,∴
备选题
一、填空题
1、sin53°cos37°+cos53°sin37°= .
2、如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径,,则的值是_____。
( http: / / www. / Index.html )
二、选择题
3、在△ABC中,∠C = 90°,∠B=50°,AB=10,则BC的长为( )
A.10tan50° B.10cos20° C.10sin50° D.
4、如图所示,AB是⊙O的直径,弦AC、BD相交于E,则等于( )
A、 B、
C、 D、
三、计算解答题
5、cos21°+cos22°+···+cos288°+cos289°.
6、如图,在梯形ABCD中,AB∥CD,∠BCD=90°,且AB=1,BC=2,tan∠ADC=2.
求证:DC=BC;
E是梯形内一点,F是梯形外一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论;
在(2)的条件下,当BE:CE=1:2,∠BEC=135°时,求sin∠BFE的值.
7、(本题12分)已知:⊙O的半径是8,直线PA,PB为⊙O的切线,A、B两点为点,
(1)当OP为何值时,∠APB=90°.
(2)若∠APB=50°,求AP的长度(结果保留三位有效数字).
(参考数据sin50°=O.7660,cos50°=0.6428,tan50°=1.1918,sin25°=0.4226,cos25°=0.9063,tan25°=O.4663)
参考答案:
1、1;2、.3、B.4、D;
5、原式=44.5
6、(1)过A作DC的垂线AM交DC于M,
则AM=BC=2.
又tan∠ADC=2,所以 HYPERLINK "http://www./Index.html" .即DC=BC.
(2)等腰三角形.
证明:因为.
所以,△DEC≌△BFC
所以,.
所以,
即△ECF是等腰直角三角形.
(3)设,则,所以.
因为,又,所以.
所以
所以.
7、(1)解:连结OA
∵PA,PB是⊙O的切线
∴∠PAO=90°,∠APO=∠BPO
∵∠APB=90°
∴∠APO=45°
∴∠AOP=45°
∴OA=PA=8
∴OP=
(2)解:连结OA
∵PA,PB是⊙O的切线
∴∠APO=∠BPO=∠APB=25°
∵ HYPERLINK "http://www./Index.html"
∴
A
B
C
C
D
B
A
O
E
