(试题2)28.2解直角三角形
文档属性
| 名称 | (试题2)28.2解直角三角形 | 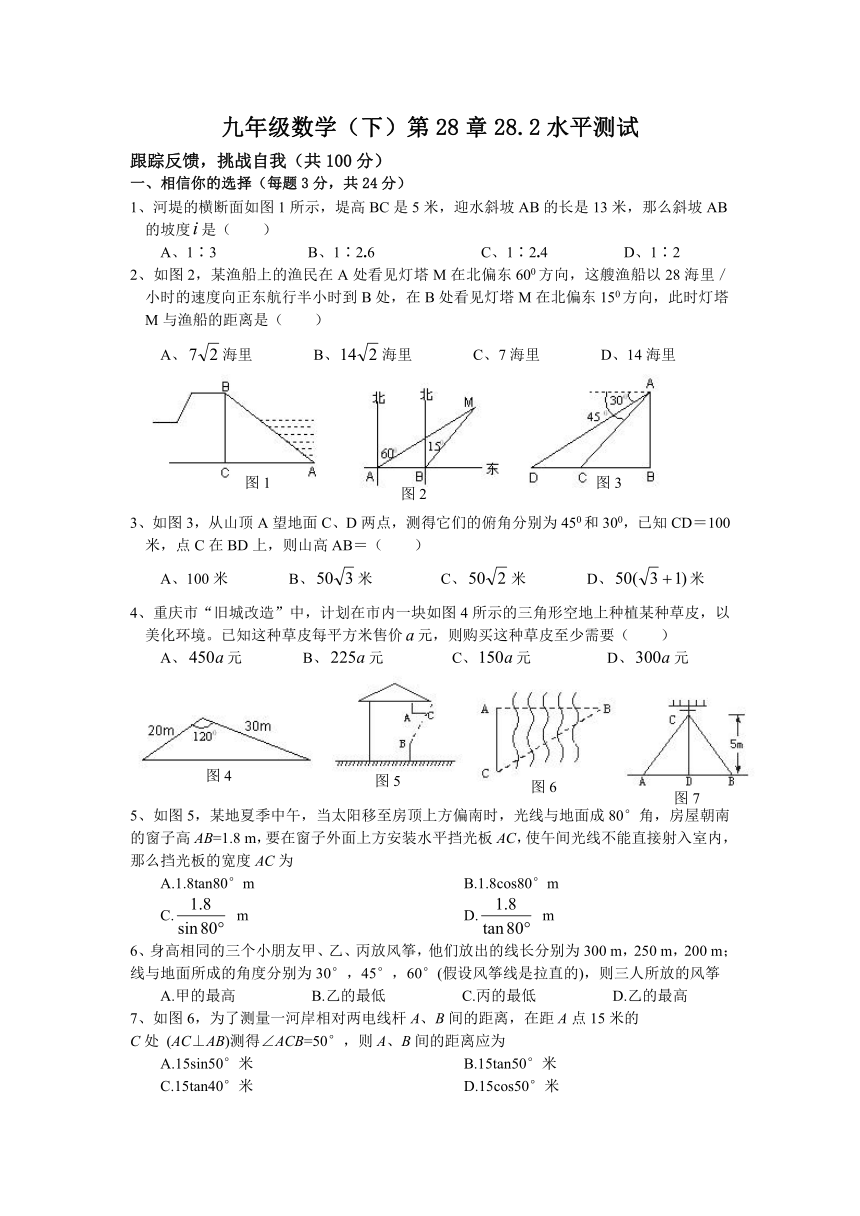 | |
| 格式 | zip | ||
| 文件大小 | 89.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-01 21:32:22 | ||
图片预览


文档简介
九年级数学(下)第28章28.2水平测试
跟踪反馈,挑战自我(共100分)
一、相信你的选择(每题3分,共24分)
1、河堤的横断面如图1所示,堤高BC是5米,迎水斜坡AB的长是13米,那么斜坡AB的坡度是( )
A、1∶3 B、1∶2.6 C、1∶2.4 D、1∶2
2、如图2,某渔船上的渔民在A处看见灯塔M在北偏东600方向,这艘渔船以28海里/小时的速度向正东航行半小时到B处,在B处看见灯塔M在北偏东150方向,此时灯塔M与渔船的距离是( )
A、海里 B、海里 C、7海里 D、14海里
3、如图3,从山顶A望地面C、D两点,测得它们的俯角分别为450和300,已知CD=100米,点C在BD上,则山高AB=( )
A、100米 B、米 C、米 D、米
4、重庆市“旧城改造”中,计划在市内一块如图4所示的三角形空地上种植某种草皮,以美化环境。已知这种草皮每平方米售价元,则购买这种草皮至少需要( )
A、元 B、元 C、元 D、元
5、如图5,某地夏季中午,当太阳移至房顶上方偏南时,光线与地面成80°角,房屋朝南的窗子高AB=1.8 m,要在窗子外面上方安装水平挡光板AC,使午间光线不能直接射入室内,那么挡光板的宽度AC为
A.1.8tan80°m B.1.8cos80°m
C. m D. m
6、身高相同的三个小朋友甲、乙、丙放风筝,他们放出的线长分别为300 m,250 m,200 m;线与地面所成的角度分别为30°,45°,60°(假设风筝线是拉直的),则三人所放的风筝
A.甲的最高 B.乙的最低 C.丙的最低 D.乙的最高
7、如图6,为了测量一河岸相对两电线杆A、B间的距离,在距A点15米的
C处 (AC⊥AB)测得∠ACB=50°,则A、B间的距离应为
A.15sin50°米 B.15tan50°米
C.15tan40°米 D.15cos50°米
8、如图7,在离地面高度5 m处引拉线固定电线杆,拉线和地面
成60°角,则拉线AC的长是
A.10 m B. HYPERLINK "http://www./Index.html" EMBED Equation.3 m C. m D.5 m
二、试试你的身手(每题3分,共24分)
1、图8表示甲、乙两山坡情况,其中tanα_____tanβ,_____坡更陡.(前一空填“>”“<”或“=”,后一空填“甲”“乙”)
2、小明要在坡度为的山坡上植树,要想保证水平株距为5 m,则相邻两株树植树地点的高度差应为_____m.
3、有一拦水坝的横断面是等腰梯形,它的上底长为6米,下底长为10米,高为2米,那么此拦水坝斜坡的坡度为_____,坡角为_____.
4、如图9,从楼顶A点测得电视塔CD的仰角为α,俯角为β,若楼房与电视塔之间的水平距离为m,求电视塔的高度.将这个实际问题写成数学形式:已知在△ADC中,AB_____CD于B,∠_____?=α,∠_____=β,m=_____,求_____.
5、要把5米长的梯子上端放在距地面3米高的阳台边沿上,猜想一下梯子摆放坡度最小为______.
6、如图10,某建筑物BC直立于水平地面,AC=9米,要建造阶梯AB,使每阶高不超过20 cm,则此阶梯最少要建_____阶.(最后一阶的高度不足20 cm时,按一阶算,取1.732)
7、小刚在一山坡上依次插了三根木杆,第一根木杆与第二根木杆插在倾斜角为30°,且坡面距离是6米的坡面上,而第二根与第三根又在倾斜角为45°,且坡面距离是8米的坡面上.则第一根与第三根木杆的水平距离是______.(如图11)(精确到0.01米)
8、如图12,小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4 m,BC=10 m,CD与地面成30°角,且此时测得1 m杆的影子长为2 m,则电线杆的高度约为_____m.(结果保留两位有效数字,≈1.41,≈1.73)
三、挑战你的技能(共52分)
1、某校在周一举行升国旗仪式,小明同学站在离旗杆
20米处(如图13所示), 随着国旗响起,五星红旗冉冉升起,
当小明同学目视国旗的仰角为37°( 假设该同学的眼睛距
地面的高度为1.6米),求此时国旗离地面的距离.
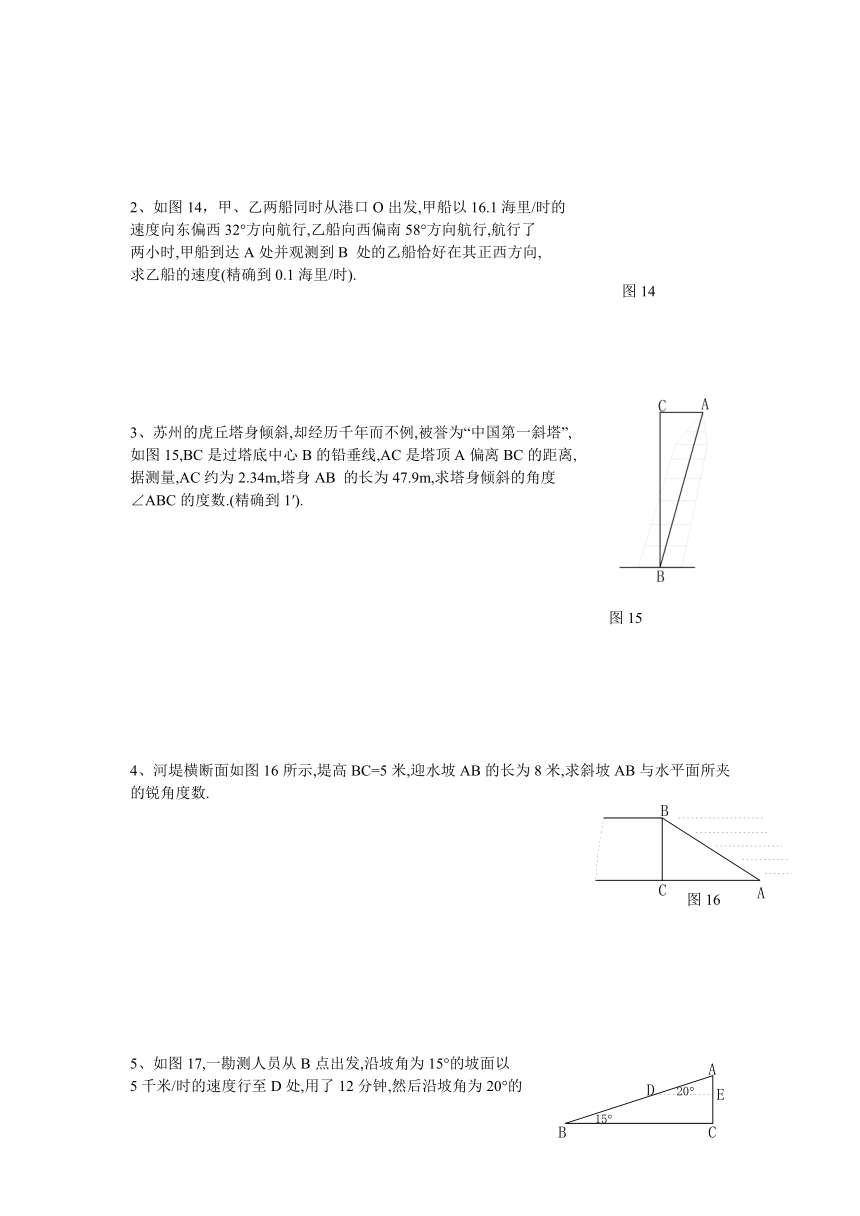
2、如图14,甲、乙两船同时从港口O出发,甲船以16.1海里/时的
速度向东偏西32°方向航行,乙船向西偏南58°方向航行,航行了
两小时,甲船到达A处并观测到B 处的乙船恰好在其正西方向,
求乙船的速度(精确到0.1海里/时).
3、苏州的虎丘塔身倾斜,却经历千年而不例,被誉为“中国第一斜塔”,
如图15,BC是过塔底中心B的铅垂线,AC是塔顶A偏离BC的距离,
据测量,AC约为2.34m,塔身AB 的长为47.9m,求塔身倾斜的角度
∠ABC的度数.(精确到1′).
4、河堤横断面如图16所示,堤高BC=5米,迎水坡AB的长为8米,求斜坡AB与水平面所夹的锐角度数.
5、如图17,一勘测人员从B点出发,沿坡角为15°的坡面以
5千米/时的速度行至D处,用了12分钟,然后沿坡角为20°的
坡面以3千米/时的速度到达山顶A点处,用了10 分钟,
求山高(即AC的长度)及A,B两点间的水平距离
(即BC的长)(精确到0.01千米).
6、如图18,在平面镜的同侧,有相隔15cm的A,B两点, 它们与平面镜的距离分别为5cm和7cm,现要使由A点射出的光线经平面镜反射后通过点B,求光线的入射角θ的度数.
提升能力,超越自我
1、在数学活动课上,老师带领学生去测河宽,如图19,
某学生在点A处观测到河对岸水边处有一点C,并测得
∠CAD=450,在距离A点30米的B处测得∠CBD=300,
求河宽CD(结果可带根号)。
2、如图20,在小山的东侧A处有一热气球,以每分钟28米的
速度沿着与垂直方向夹角为300的方向飞行,半小时后到达C处,
这时气球上的人发现,在A处的正西方向有一处着火点B,5分钟后,
在D处测得着火点B的府角是150,求热气球升空点A与着火点B
的距离。(结果保留根号,参考数据:,
,,)
3、一艘轮船从西向东航行,上午10时航行到点A处,此时测得在
船北偏东30°上有一灯塔B,到11时测得灯塔B正好在船的正北
方向,此时轮船所处位置为C点 (如图21),若该船的航行速度为
每小时20海里,那么船在C点时距离灯塔B多远?(取1.73)
4、如图22,河岸护堤AD、BC互相平行,要测量河两岸相对
两树A、B的距离,小赵从B点沿垂直AB的BC方向前进,
他手中有足够长的米尺和含有30°角的一块三角板.
(1)请你帮小赵设计一下测量AB长的具体方案;
(2)给出具体的数值,求出AB的长.
5、如图23,在一座高为10 m的大楼顶C测得旗杆底部B的俯角α为60°,
旗杆顶端A的仰角β为20°(取1.73,tan20°≈0.3646)
(1)求建筑物与旗杆的水平距离BD;
(2)计算旗杆高.(精确到0.1 m)
参考答案:
A卷
一、选择题:
1、C;2、A;3、D;4、C;5、D;6、D;1、B;2、B;
二、填空题:
1、< 乙;2、3;3、 600;4、⊥ BAC BAD AB CD;5、;6、26;
7、10.85;8、8.7;
三、解答题
1、由已知得,∠ADE=37°,DE=BC=20米,CD=1.6米,BE=1.6米,
在Rt△ADE中,AE=DEtan37°=20×0.7536=15.07(米)≈15.1(米).
故AB=15.1+1.6=16.7(米). 即国旗离地面约16.7米.
2、由已知得:∠AOB=90°,∠A=32°,OA=16.1×2=32.2(海里).
∴OB=OA.tanA= 32.2×tan32°=32.2×0.6249≈20.12(海里).
故乙船的速度为20.12÷2≈10.1(海里/时).
3、sin∠ABC=≈0.0489,得∠ABC=2°48′.
即塔身倾斜的角度为2°48′.
4、sinA==0.625,∠A≈38°40′56″.
5、过D作DF⊥BC于F.由已知得BD=5×=1(千米),AD=3×=0.5(千米).
在Rt △BFD中,DF=BD·sin15°≈0.2588(千米),
BF=BD·cos15°≈0.9659(千米),
在Rt△ADE 中,DE=AD·cos20°≈0.4698(千米).
AE=AD·sin20°≈0.1710(千米).
故AC=AE+EC=AE+ DF=0.1710+0.2588=0.4298≈0.43(千米),
BC=BF+CF=BF+DE=0.9659+0.4698=1.4357≈1.44(千米).
6、过A作AG⊥BF于G,则BG=7-5=2,
故EF=AG=.
又由已知得∠EAD=∠DBF=θ,
故EF= ED+DF=5tanθ+7tanθ=12tanθ,
故tanθ=,
由此得 θ≈51.1°.
提升能力,超越自我
1、米;
2、米;
3、解:由题意知∠BAC=60°,∠C=90°,
AC=20×(11-10)=20(海里).
∴tanBAC=,即tan60°=.
∴BC=20tan60°=20≈34.6(海里).
4、(1)方案:至某点C时,三角板60°角一直角边与BC重合,另一边与AC重合,然后用米尺量出BC的长度,此法就可求出AB的长.
(2)设BC=10米,∠C=60°,
则在Rt△ABC中,tanC=,
∴AB=BC·tan60°=10×=10(米).
5、解:(1)∵∠CBD=α=60°,
∴在Rt△BDC中,
tanCBD=.
∴BD=== (m).
(2)设CE⊥AB,垂足为E,
∴CE=BD=(m).
在Rt△AEC中,
∵tanβ=,
∴AE=CE·tanβ= HYPERLINK "http://www./Index.html" EMBED Equation.3 ·tan20°≈2.1(m).
∴AB=2.1+10=12.1(m),即旗杆高为12.1 m.
图3
图2
图1
图7
图6
图5
图4
图10
图8
图9
图11
图12
图13
图14
图15
图16
图17
图18
图19
图20
图21
图22
图23
跟踪反馈,挑战自我(共100分)
一、相信你的选择(每题3分,共24分)
1、河堤的横断面如图1所示,堤高BC是5米,迎水斜坡AB的长是13米,那么斜坡AB的坡度是( )
A、1∶3 B、1∶2.6 C、1∶2.4 D、1∶2
2、如图2,某渔船上的渔民在A处看见灯塔M在北偏东600方向,这艘渔船以28海里/小时的速度向正东航行半小时到B处,在B处看见灯塔M在北偏东150方向,此时灯塔M与渔船的距离是( )
A、海里 B、海里 C、7海里 D、14海里
3、如图3,从山顶A望地面C、D两点,测得它们的俯角分别为450和300,已知CD=100米,点C在BD上,则山高AB=( )
A、100米 B、米 C、米 D、米
4、重庆市“旧城改造”中,计划在市内一块如图4所示的三角形空地上种植某种草皮,以美化环境。已知这种草皮每平方米售价元,则购买这种草皮至少需要( )
A、元 B、元 C、元 D、元
5、如图5,某地夏季中午,当太阳移至房顶上方偏南时,光线与地面成80°角,房屋朝南的窗子高AB=1.8 m,要在窗子外面上方安装水平挡光板AC,使午间光线不能直接射入室内,那么挡光板的宽度AC为
A.1.8tan80°m B.1.8cos80°m
C. m D. m
6、身高相同的三个小朋友甲、乙、丙放风筝,他们放出的线长分别为300 m,250 m,200 m;线与地面所成的角度分别为30°,45°,60°(假设风筝线是拉直的),则三人所放的风筝
A.甲的最高 B.乙的最低 C.丙的最低 D.乙的最高
7、如图6,为了测量一河岸相对两电线杆A、B间的距离,在距A点15米的
C处 (AC⊥AB)测得∠ACB=50°,则A、B间的距离应为
A.15sin50°米 B.15tan50°米
C.15tan40°米 D.15cos50°米
8、如图7,在离地面高度5 m处引拉线固定电线杆,拉线和地面
成60°角,则拉线AC的长是
A.10 m B. HYPERLINK "http://www./Index.html" EMBED Equation.3 m C. m D.5 m
二、试试你的身手(每题3分,共24分)
1、图8表示甲、乙两山坡情况,其中tanα_____tanβ,_____坡更陡.(前一空填“>”“<”或“=”,后一空填“甲”“乙”)
2、小明要在坡度为的山坡上植树,要想保证水平株距为5 m,则相邻两株树植树地点的高度差应为_____m.
3、有一拦水坝的横断面是等腰梯形,它的上底长为6米,下底长为10米,高为2米,那么此拦水坝斜坡的坡度为_____,坡角为_____.
4、如图9,从楼顶A点测得电视塔CD的仰角为α,俯角为β,若楼房与电视塔之间的水平距离为m,求电视塔的高度.将这个实际问题写成数学形式:已知在△ADC中,AB_____CD于B,∠_____?=α,∠_____=β,m=_____,求_____.
5、要把5米长的梯子上端放在距地面3米高的阳台边沿上,猜想一下梯子摆放坡度最小为______.
6、如图10,某建筑物BC直立于水平地面,AC=9米,要建造阶梯AB,使每阶高不超过20 cm,则此阶梯最少要建_____阶.(最后一阶的高度不足20 cm时,按一阶算,取1.732)
7、小刚在一山坡上依次插了三根木杆,第一根木杆与第二根木杆插在倾斜角为30°,且坡面距离是6米的坡面上,而第二根与第三根又在倾斜角为45°,且坡面距离是8米的坡面上.则第一根与第三根木杆的水平距离是______.(如图11)(精确到0.01米)
8、如图12,小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4 m,BC=10 m,CD与地面成30°角,且此时测得1 m杆的影子长为2 m,则电线杆的高度约为_____m.(结果保留两位有效数字,≈1.41,≈1.73)
三、挑战你的技能(共52分)
1、某校在周一举行升国旗仪式,小明同学站在离旗杆
20米处(如图13所示), 随着国旗响起,五星红旗冉冉升起,
当小明同学目视国旗的仰角为37°( 假设该同学的眼睛距
地面的高度为1.6米),求此时国旗离地面的距离.
2、如图14,甲、乙两船同时从港口O出发,甲船以16.1海里/时的
速度向东偏西32°方向航行,乙船向西偏南58°方向航行,航行了
两小时,甲船到达A处并观测到B 处的乙船恰好在其正西方向,
求乙船的速度(精确到0.1海里/时).
3、苏州的虎丘塔身倾斜,却经历千年而不例,被誉为“中国第一斜塔”,
如图15,BC是过塔底中心B的铅垂线,AC是塔顶A偏离BC的距离,
据测量,AC约为2.34m,塔身AB 的长为47.9m,求塔身倾斜的角度
∠ABC的度数.(精确到1′).
4、河堤横断面如图16所示,堤高BC=5米,迎水坡AB的长为8米,求斜坡AB与水平面所夹的锐角度数.
5、如图17,一勘测人员从B点出发,沿坡角为15°的坡面以
5千米/时的速度行至D处,用了12分钟,然后沿坡角为20°的
坡面以3千米/时的速度到达山顶A点处,用了10 分钟,
求山高(即AC的长度)及A,B两点间的水平距离
(即BC的长)(精确到0.01千米).
6、如图18,在平面镜的同侧,有相隔15cm的A,B两点, 它们与平面镜的距离分别为5cm和7cm,现要使由A点射出的光线经平面镜反射后通过点B,求光线的入射角θ的度数.
提升能力,超越自我
1、在数学活动课上,老师带领学生去测河宽,如图19,
某学生在点A处观测到河对岸水边处有一点C,并测得
∠CAD=450,在距离A点30米的B处测得∠CBD=300,
求河宽CD(结果可带根号)。
2、如图20,在小山的东侧A处有一热气球,以每分钟28米的
速度沿着与垂直方向夹角为300的方向飞行,半小时后到达C处,
这时气球上的人发现,在A处的正西方向有一处着火点B,5分钟后,
在D处测得着火点B的府角是150,求热气球升空点A与着火点B
的距离。(结果保留根号,参考数据:,
,,)
3、一艘轮船从西向东航行,上午10时航行到点A处,此时测得在
船北偏东30°上有一灯塔B,到11时测得灯塔B正好在船的正北
方向,此时轮船所处位置为C点 (如图21),若该船的航行速度为
每小时20海里,那么船在C点时距离灯塔B多远?(取1.73)
4、如图22,河岸护堤AD、BC互相平行,要测量河两岸相对
两树A、B的距离,小赵从B点沿垂直AB的BC方向前进,
他手中有足够长的米尺和含有30°角的一块三角板.
(1)请你帮小赵设计一下测量AB长的具体方案;
(2)给出具体的数值,求出AB的长.
5、如图23,在一座高为10 m的大楼顶C测得旗杆底部B的俯角α为60°,
旗杆顶端A的仰角β为20°(取1.73,tan20°≈0.3646)
(1)求建筑物与旗杆的水平距离BD;
(2)计算旗杆高.(精确到0.1 m)
参考答案:
A卷
一、选择题:
1、C;2、A;3、D;4、C;5、D;6、D;1、B;2、B;
二、填空题:
1、< 乙;2、3;3、 600;4、⊥ BAC BAD AB CD;5、;6、26;
7、10.85;8、8.7;
三、解答题
1、由已知得,∠ADE=37°,DE=BC=20米,CD=1.6米,BE=1.6米,
在Rt△ADE中,AE=DEtan37°=20×0.7536=15.07(米)≈15.1(米).
故AB=15.1+1.6=16.7(米). 即国旗离地面约16.7米.
2、由已知得:∠AOB=90°,∠A=32°,OA=16.1×2=32.2(海里).
∴OB=OA.tanA= 32.2×tan32°=32.2×0.6249≈20.12(海里).
故乙船的速度为20.12÷2≈10.1(海里/时).
3、sin∠ABC=≈0.0489,得∠ABC=2°48′.
即塔身倾斜的角度为2°48′.
4、sinA==0.625,∠A≈38°40′56″.
5、过D作DF⊥BC于F.由已知得BD=5×=1(千米),AD=3×=0.5(千米).
在Rt △BFD中,DF=BD·sin15°≈0.2588(千米),
BF=BD·cos15°≈0.9659(千米),
在Rt△ADE 中,DE=AD·cos20°≈0.4698(千米).
AE=AD·sin20°≈0.1710(千米).
故AC=AE+EC=AE+ DF=0.1710+0.2588=0.4298≈0.43(千米),
BC=BF+CF=BF+DE=0.9659+0.4698=1.4357≈1.44(千米).
6、过A作AG⊥BF于G,则BG=7-5=2,
故EF=AG=.
又由已知得∠EAD=∠DBF=θ,
故EF= ED+DF=5tanθ+7tanθ=12tanθ,
故tanθ=,
由此得 θ≈51.1°.
提升能力,超越自我
1、米;
2、米;
3、解:由题意知∠BAC=60°,∠C=90°,
AC=20×(11-10)=20(海里).
∴tanBAC=,即tan60°=.
∴BC=20tan60°=20≈34.6(海里).
4、(1)方案:至某点C时,三角板60°角一直角边与BC重合,另一边与AC重合,然后用米尺量出BC的长度,此法就可求出AB的长.
(2)设BC=10米,∠C=60°,
则在Rt△ABC中,tanC=,
∴AB=BC·tan60°=10×=10(米).
5、解:(1)∵∠CBD=α=60°,
∴在Rt△BDC中,
tanCBD=.
∴BD=== (m).
(2)设CE⊥AB,垂足为E,
∴CE=BD=(m).
在Rt△AEC中,
∵tanβ=,
∴AE=CE·tanβ= HYPERLINK "http://www./Index.html" EMBED Equation.3 ·tan20°≈2.1(m).
∴AB=2.1+10=12.1(m),即旗杆高为12.1 m.
图3
图2
图1
图7
图6
图5
图4
图10
图8
图9
图11
图12
图13
图14
图15
图16
图17
图18
图19
图20
图21
图22
图23
