29.2三视图
图片预览

文档简介
29.2三视图
学习目标
1.了解基本几何体与其三视图、展开图(球除外)之间的关系;经过典型实例,知道这种关系在现实生活中的应用(如物体的包装)。
2.根据所给的简单几何体准确地画出三视图。
3.根据三视图想象出物体的形状,并进行相应的表面积或体积计算。
基础练习一
1.三视图的位置有规定,主视图要在 边,它的下方应是 图,左视图坐落在 边。左视图的左 俯视 主视图的右
2.主视图反映物体的 和 ,俯视图反映物体的 和 ,左视图反映物体的 和 。长高 长宽 高宽
3.从一个楼房的三视图中, 图可以反映楼房的高度。主视图或左视
4.画视图时,看得见的轮廓线通常画成 ,看不见的部分通常画成 。
5.如图几何体的左视图是( B )
6.如图所示,圆柱的俯视图是( C )
图 A B C D
7.由几个小立方体搭成的一个几何
体如图1所示,它的主(正)视图
见图2,那么它的俯视图为( C )
8. 下列物体中,主视图为图1的是 ( B )
9.如图放置的圆锥,它的主视图、俯视图、左视图分别为( B )
综合应用一
请你在图2中补全如图所示的
圆锥形纸帽的三种视图.
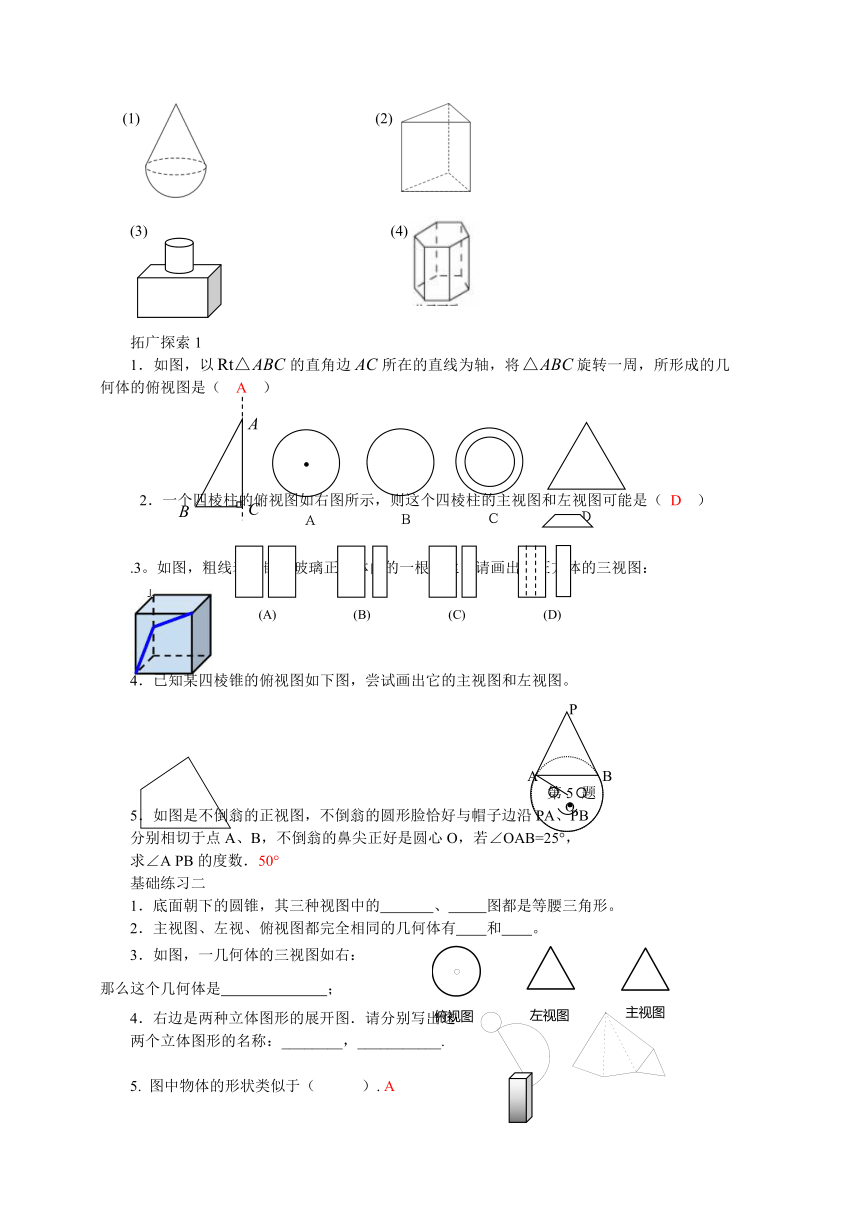
2.画出下列立体图形的三视图。
(1) (2)
(3) (4)
拓广探索1
1.如图,以的直角边所在的直线为轴,将旋转一周,所形成的几何体的俯视图是( A )
2.一个四棱柱的俯视图如右图所示,则这个四棱柱的主视图和左视图可能是( D )
.3。如图,粗线表示嵌在玻璃正方体内的一根铁丝,请画出该正方体的三视图:
4.已知某四棱锥的俯视图如下图,尝试画出它的主视图和左视图。
第5 题
5.如图是不倒翁的正视图,不倒翁的圆形脸恰好与帽子边沿PA、PB
分别相切于点A、B,不倒翁的鼻尖正好是圆心O,若∠OAB=25°,
求∠A PB的度数.50°
基础练习二
1.底面朝下的圆锥,其三种视图中的 、 图都是等腰三角形。
2.主视图、左视、俯视图都完全相同的几何体有 和 。
3.如图,一几何体的三视图如右:
那么这个几何体是 ;
4.右边是两种立体图形的展开图.请分别写出这
两个立体图形的名称:________,___________.
5. 图中物体的形状类似于( ). A
(A)棱柱 (B)圆柱 (C)圆锥 (D)球
6.如果某物体的三视图是如图所示的
三个图形,那么该物体的形状是( )
C
A、正方体 B、长方体 C、三棱柱 D、圆锥
7.一张桌子摆放若干碟子,从三个方向上看,三种视图如下图所示,则这张桌子上共有 个碟子;
12
8.右图是由一些相同的小正方体构成的几何体的俯视
图,则构成这个几何体的小正方体的最少个数是( )
A.5 B.6 C.7 D.8 C
9.如果用□表示1个立方体,用表示两个立方体叠加,用■表示三个立方体叠加,那么下面右图由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是 ( )B
综合应用二
1.用连线的方法,根据下列主视图和俯视图,找出对应物体
2.如图是一个物体的三视图,请画出物体的形状。
3.根据下面三视图建造的建筑物是什么样子的?共有几层?一共需要多少个小正方体。
4.根据物体的三视图,描述及画出物体的形状
基础练习三
1.平面展开图是四个长方形和两个正方形的立体图形是 。正四棱柱
2.圆柱的平面展开图是一个 和两个 。矩形,圆
3.圆锥的平面展开图是一个 和 。扇形,一个圆
4.一个几何体由一个直角三直角绕着斜边旋转一周得到,那么这个几何体的平面展开图是 。两个扇形
5.边长为6的正六边形的半径是 ,边心距是 ,面积是 (用根号表示) 6,3 ,54
6.底圆半径是r,母线长l的的圆锥的侧面积是 。πrl
7.如图,已知圆柱体底面圆的半径为,高为2,AB、CD分别是两底面的直径,AD、BC是母线,若一只小虫从A点出发,从侧面爬行到C点,则小虫爬行的最短路线的长度是 (结果保留根式).
8.如图是一口直径AB为4米,深BC为2米的圆柱形养蛙池,
小青蛙们晚上经常坐在池底中心O观赏月亮,则它们看见月亮的最
大视角∠COD= 度,(不考虑青蛙的身高) 90
9.右图是某个物体的俯视图,它是一个腰为20mm的等腰直角
三直角形,这个物体的高是100mm,那么它的体积是 mm3。
(用科学计数法表示)
综合练习二
1.想一想,哪种几何体的表面展开成如下的平面图形,画出表示这些几何体的立体图形.并根据相关数据计算其侧面积。
(1) 边长是12mm,高为60mm
(2) 底圆半径是20mm,高是50mm
2.这是某玩具厂的一块积木的三视图,
现要在它的表面上油漆,需要上油漆的面积是多少?
15
36
20 3.这是一个燕尾槽的三视图,(1) 补全这个三视图;(2) 根据 图上数据计算其体积
50
30
60 80
100 20
4。(1) 画出下列物体的三视图;(2)如果要给这个几何电镀,那么电镀的面积是多少?(注意:小圆直径是20 ,请在图上画出)
50 30
80
答案:基础训练一 1,左视图的左,视图,主视图的右 2,长,高,长,宽,高,宽 3,主视(或左视图) 4,实线,虚线 5,B 6,C 7,C 8,B 9,B 综合应用一 1,略 2,(1)
(2) (3)略 (4)
拓广探索一 1,A 2,D
3, 4,
5,50°基础练习二 1,主视图和左视图 2,球,正方体 3,圆锥 4,圆锥,三棱锥 5,A 6,C 7,12 8,C 9,B 综合应用二 1,略 2,
3,图略,共三层,需9个小正方体
4,图略,物体是底为等腰梯形的四棱柱
基础练习三 1,正四棱柱 2,矩形,圆 3,扇形,一个圆 4,两个扇形 5,6,3 ,54 6,πrl 7, 8,90°9,2×104 综合应用二 1,(1)3600mm2(2)2000πmm2 2,9840mm2 3,(1)图略 (2)体积=100×80×20-0.5×(30+60)×(80-50)=1350mm3 4,(1)图略 (2)2×50×80+2×50×30+80×30+0。5×80π×30+402π-2×102π+20π×30=(13400+3200π)mm2=(134+32π)cm2
A.
B.
C.
D.
左视图
A
B
C
D
(A)
(B)
(C)
(D)
·
P
A
B
O
俯视图
主视图
左视图
主视图
左视图
俯视图
主视图
左视图
俯视图
学习目标
1.了解基本几何体与其三视图、展开图(球除外)之间的关系;经过典型实例,知道这种关系在现实生活中的应用(如物体的包装)。
2.根据所给的简单几何体准确地画出三视图。
3.根据三视图想象出物体的形状,并进行相应的表面积或体积计算。
基础练习一
1.三视图的位置有规定,主视图要在 边,它的下方应是 图,左视图坐落在 边。左视图的左 俯视 主视图的右
2.主视图反映物体的 和 ,俯视图反映物体的 和 ,左视图反映物体的 和 。长高 长宽 高宽
3.从一个楼房的三视图中, 图可以反映楼房的高度。主视图或左视
4.画视图时,看得见的轮廓线通常画成 ,看不见的部分通常画成 。
5.如图几何体的左视图是( B )
6.如图所示,圆柱的俯视图是( C )
图 A B C D
7.由几个小立方体搭成的一个几何
体如图1所示,它的主(正)视图
见图2,那么它的俯视图为( C )
8. 下列物体中,主视图为图1的是 ( B )
9.如图放置的圆锥,它的主视图、俯视图、左视图分别为( B )
综合应用一
请你在图2中补全如图所示的
圆锥形纸帽的三种视图.
2.画出下列立体图形的三视图。
(1) (2)
(3) (4)
拓广探索1
1.如图,以的直角边所在的直线为轴,将旋转一周,所形成的几何体的俯视图是( A )
2.一个四棱柱的俯视图如右图所示,则这个四棱柱的主视图和左视图可能是( D )
.3。如图,粗线表示嵌在玻璃正方体内的一根铁丝,请画出该正方体的三视图:
4.已知某四棱锥的俯视图如下图,尝试画出它的主视图和左视图。
第5 题
5.如图是不倒翁的正视图,不倒翁的圆形脸恰好与帽子边沿PA、PB
分别相切于点A、B,不倒翁的鼻尖正好是圆心O,若∠OAB=25°,
求∠A PB的度数.50°
基础练习二
1.底面朝下的圆锥,其三种视图中的 、 图都是等腰三角形。
2.主视图、左视、俯视图都完全相同的几何体有 和 。
3.如图,一几何体的三视图如右:
那么这个几何体是 ;
4.右边是两种立体图形的展开图.请分别写出这
两个立体图形的名称:________,___________.
5. 图中物体的形状类似于( ). A
(A)棱柱 (B)圆柱 (C)圆锥 (D)球
6.如果某物体的三视图是如图所示的
三个图形,那么该物体的形状是( )
C
A、正方体 B、长方体 C、三棱柱 D、圆锥
7.一张桌子摆放若干碟子,从三个方向上看,三种视图如下图所示,则这张桌子上共有 个碟子;
12
8.右图是由一些相同的小正方体构成的几何体的俯视
图,则构成这个几何体的小正方体的最少个数是( )
A.5 B.6 C.7 D.8 C
9.如果用□表示1个立方体,用表示两个立方体叠加,用■表示三个立方体叠加,那么下面右图由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是 ( )B
综合应用二
1.用连线的方法,根据下列主视图和俯视图,找出对应物体
2.如图是一个物体的三视图,请画出物体的形状。
3.根据下面三视图建造的建筑物是什么样子的?共有几层?一共需要多少个小正方体。
4.根据物体的三视图,描述及画出物体的形状
基础练习三
1.平面展开图是四个长方形和两个正方形的立体图形是 。正四棱柱
2.圆柱的平面展开图是一个 和两个 。矩形,圆
3.圆锥的平面展开图是一个 和 。扇形,一个圆
4.一个几何体由一个直角三直角绕着斜边旋转一周得到,那么这个几何体的平面展开图是 。两个扇形
5.边长为6的正六边形的半径是 ,边心距是 ,面积是 (用根号表示) 6,3 ,54
6.底圆半径是r,母线长l的的圆锥的侧面积是 。πrl
7.如图,已知圆柱体底面圆的半径为,高为2,AB、CD分别是两底面的直径,AD、BC是母线,若一只小虫从A点出发,从侧面爬行到C点,则小虫爬行的最短路线的长度是 (结果保留根式).
8.如图是一口直径AB为4米,深BC为2米的圆柱形养蛙池,
小青蛙们晚上经常坐在池底中心O观赏月亮,则它们看见月亮的最
大视角∠COD= 度,(不考虑青蛙的身高) 90
9.右图是某个物体的俯视图,它是一个腰为20mm的等腰直角
三直角形,这个物体的高是100mm,那么它的体积是 mm3。
(用科学计数法表示)
综合练习二
1.想一想,哪种几何体的表面展开成如下的平面图形,画出表示这些几何体的立体图形.并根据相关数据计算其侧面积。
(1) 边长是12mm,高为60mm
(2) 底圆半径是20mm,高是50mm
2.这是某玩具厂的一块积木的三视图,
现要在它的表面上油漆,需要上油漆的面积是多少?
15
36
20 3.这是一个燕尾槽的三视图,(1) 补全这个三视图;(2) 根据 图上数据计算其体积
50
30
60 80
100 20
4。(1) 画出下列物体的三视图;(2)如果要给这个几何电镀,那么电镀的面积是多少?(注意:小圆直径是20 ,请在图上画出)
50 30
80
答案:基础训练一 1,左视图的左,视图,主视图的右 2,长,高,长,宽,高,宽 3,主视(或左视图) 4,实线,虚线 5,B 6,C 7,C 8,B 9,B 综合应用一 1,略 2,(1)
(2) (3)略 (4)
拓广探索一 1,A 2,D
3, 4,
5,50°基础练习二 1,主视图和左视图 2,球,正方体 3,圆锥 4,圆锥,三棱锥 5,A 6,C 7,12 8,C 9,B 综合应用二 1,略 2,
3,图略,共三层,需9个小正方体
4,图略,物体是底为等腰梯形的四棱柱
基础练习三 1,正四棱柱 2,矩形,圆 3,扇形,一个圆 4,两个扇形 5,6,3 ,54 6,πrl 7, 8,90°9,2×104 综合应用二 1,(1)3600mm2(2)2000πmm2 2,9840mm2 3,(1)图略 (2)体积=100×80×20-0.5×(30+60)×(80-50)=1350mm3 4,(1)图略 (2)2×50×80+2×50×30+80×30+0。5×80π×30+402π-2×102π+20π×30=(13400+3200π)mm2=(134+32π)cm2
A.
B.
C.
D.
左视图
A
B
C
D
(A)
(B)
(C)
(D)
·
P
A
B
O
俯视图
主视图
左视图
主视图
左视图
俯视图
主视图
左视图
俯视图
