1.1 直角三角形的性质和判定 课件(共20张PPT)
文档属性
| 名称 | 1.1 直角三角形的性质和判定 课件(共20张PPT) |

|
|
| 格式 | rar | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
直角三角形的性质和判定
湘教版·八年级数学下册
上课课件
第一章
【知识与技能】
1.体验直角三角形应用的广泛性,理解直角三角形的定义,进一步认识直角三角形.
2.学会用符号和字母表示直角三角形.
3.经历“直角三角形两个锐角互余”的探讨,掌握直角三角形两个锐角互余的性质.
4.会用“两个锐角互余的三角形是直角三角形”这个判定方法判定直角三角形.
5.理解和掌握直角三角形性质“斜边上的中线等于斜边的一半”.
【过程与方法】
通过动手,猜想发现直角三角形的性质,引导逆向思维,探索性质的推导方法——同一法.
【情感态度】
体会从“一般到特殊”的思维方法和“逆向思维”方法,培养逆向思维能力.
【教学重点】
直角三角形性质和判定的探索及应用.
【教学难点】
直角三角形性质“斜边上的中线等于斜边的一半”的判定探索过程.
学习目标
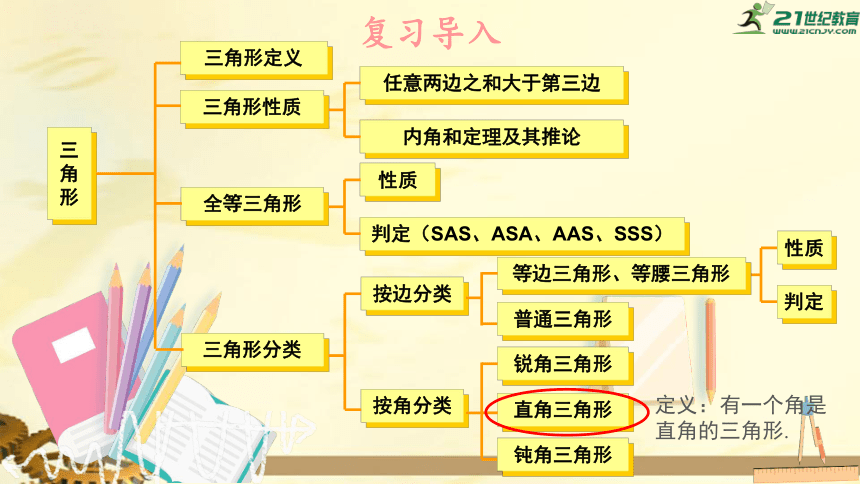
复习导入
三角形定义
三
角
形
三角形性质
按边分类
按角分类
全等三角形
三角形分类
任意两边之和大于第三边
内角和定理及其推论
性质
判定(SAS、ASA、AAS、SSS)
锐角三角形
直角三角形
钝角三角形
性质
判定
等边三角形、等腰三角形
普通三角形
定义:有一个角是直角的三角形.
新课引入
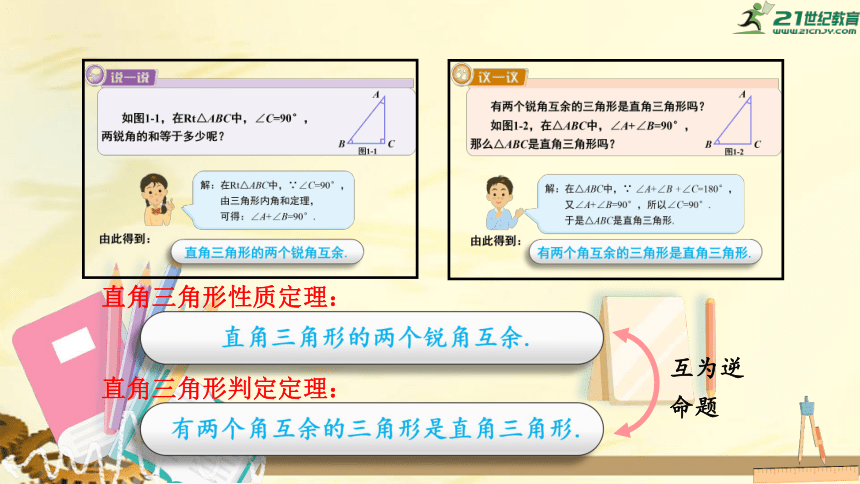
如图1-1,在Rt△ABC中,∠C=90°,两锐角的和等于多少呢?
A
B
C
图1-1
解:在Rt△ABC中,∵∠C=90°,
由三角形内角和定理,
可得:∠A+∠B=90°.
由此得到:
直角三角形的两个锐角互余.
Rt△两锐角关系动态演示
几何画
板.gsp
随堂跟练
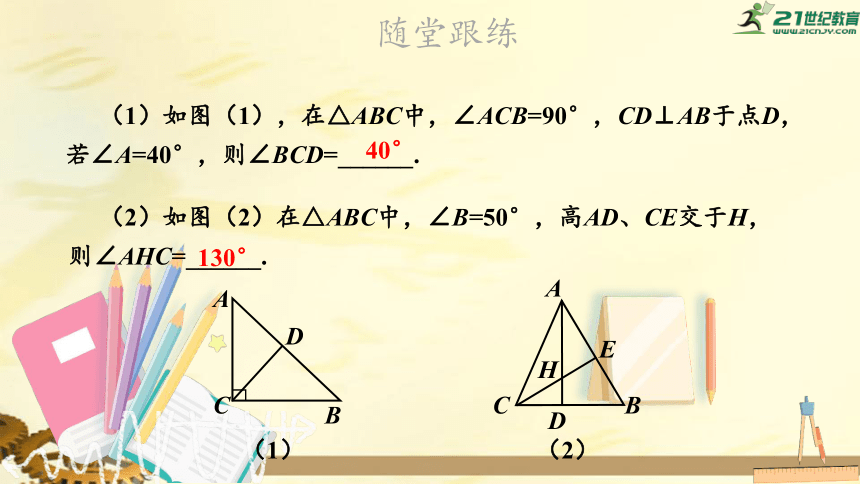
(1)如图(1),在△ABC中,∠ACB=90°,CD⊥AB于点D,若∠A=40°,则∠BCD=______.
(2)如图(2)在△ABC中,∠B=50°,高AD、CE交于H,则∠AHC=______.
40°
130°
A
C
D
B
(1)
A
C
B
D
H
E
(2)
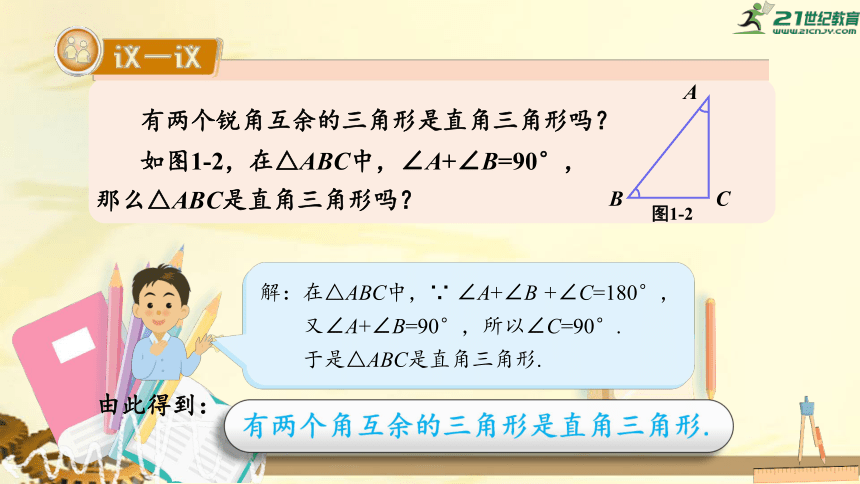
有两个锐角互余的三角形是直角三角形吗?
A
B
C
图1-2
如图1-2,在△ABC中,∠A+∠B=90°,
那么△ABC是直角三角形吗?
解:在△ABC中,∵
∠A+∠B
+∠C=180°,
又∠A+∠B=90°,所以∠C=90°.
于是△ABC是直角三角形.
由此得到:
有两个角互余的三角形是直角三角形.
随堂跟练
(3)如图,AB∥CD,∠CAB和∠ACD的平分线相交于H点,那么△AHC是直角三角形吗?为什么?
A
B
C
D
H
解:∵AB//
CD,
∴∠
CAB+∠ACD=180°.
又∠CAH=
∠CAB,∠ACH=
∠ACD,
∴∠CAH+∠ACH
=
(∠CAB+∠ACD)=90°.
∴△AHC是直角三角形.
直角三角形的两个锐角互余.
直角三角形性质定理:
直角三角形判定定理:
有两个角互余的三角形是直角三角形.
互为逆命题
我测量后发现
探究新知
A
B
C
图1-3
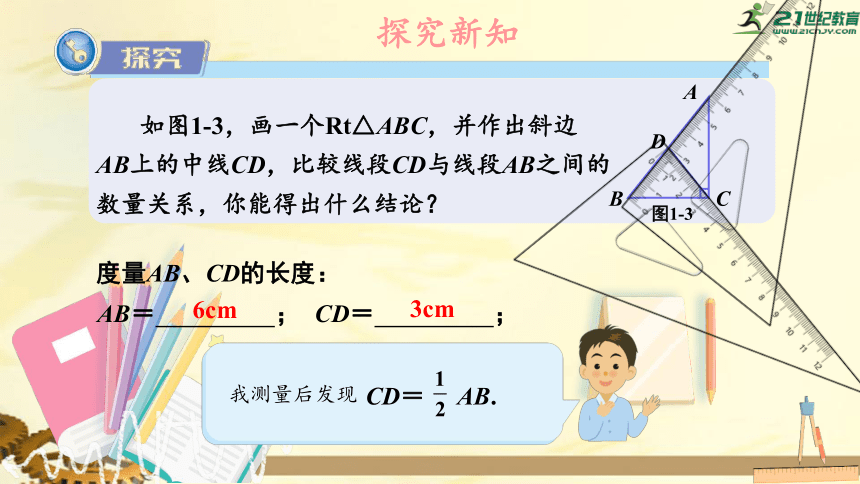
如图1-3,画一个Rt△ABC,并作出斜边AB上的中线CD,比较线段CD与线段AB之间的数量关系,你能得出什么结论?
D
AB=
;
CD=
;
度量AB、CD的长度:
6cm
3cm
CD=
AB.
Rt△中线与斜边关系动态演示
几何画
板.gsp
探究新知
由此得到:
直角三角形斜边上的中线等于斜边的一半.
是否对于任意一个Rt△ABC,都有
?
CD=
AB
A
B
图1-4
D
C
E
F
证明:如图1-4,过点D作DE⊥AC,交AC于点E;作DF⊥BC,交BC于点F.
∵∠ACB=
∠AED=∠DFB
=
90°,
∴DE//
BC,DF//AC.
∴∠A=∠FDB,∠ADE=∠B.
又D为AB的中点,即AD=DB,
∴△AED≌△DFB
(ASA).
∴AE=DF,
DE=
BF.
同理可证△CDE≌△DCF,
从而DE=CF,CE=
DF.
∴AE=CE,BF=
CF.
故DE,
DF分别垂直平分边AC,
BC.
AD=CD=BD
(为什么?)
.
由此得到:CD=
AB
例
1
如图1-5,已知CD是△ABC的AB边上的中线,且CD=
AB.求证:△ABC是直角三角形.
A
B
图1-5
D
C
1
2
证明:∵CD=
AB=AD=BD,
∴∠1=∠A,∠2=∠B.
∵∠A+∠B+∠ACB=180°,
∠ACB=∠1+∠2
∴∠A+∠B
+∠1+∠2
=180°.
∴2(
∠A+∠B
)=180°.
∴∠A+∠B=90°.
∴△ABC是直角三角形.
(等边对等角)
(三角形内角和的性质)
(有两个角互余的三角形是直角三角形)
由此得到:___________________________________________________________
三角形一边上的中线等于这条边的一半的三角形是直角三角形.
直角三角形斜边上的中线等于斜边的一半.
三角形一边上的中线等于这条边的一半的三角形是直角三角形.
直角三角形性质定理:
直角三角形判定定理:
互为逆命题
巩固练习
1.在Rt△ABC中,斜边上的中线CD=2.5cm,则斜边AB的长是多少?
直角三角形斜边上的中线等于斜边的一半.
直角三角形性质定理:
AB=5cm
A
B
D
C
巩固练习
2.如图,AB∥CD,∠CAB和∠ACD的平分线相交于H点,E为AC的中点,EH=2.那么△AHC是直角三角形吗?为什么?若是,求出AC的长.
解:△AHC是直角三角形,理由:
∵AB∥CD,∴∠CAB+∠ACD=180°.
∵AH,CH分别为∠CAB,∠ACD的平分线,
∴∠CAH+∠ACH=90°.
∴∠AHC=90°,即△AHC是直角三角形.
∵E为AC的中点,∴AC=2EH=4.
巩固练习
1.如图,CD是Rt△ABC的中线,∠ACB=90°,
∠CDA
=120°,求∠B的度数.
解:∵CD是Rt△ABC斜边AB上的中线,
∴CD=DB=AD.
∵∠CDA=120°,
∴∠A=∠ACD=30°.
在Rt△ABC中,∠A+∠B=90°,∴∠B=60°.
巩固练习
2.如图,在△ABC中,已知∠B=
∠A=
∠C,AB=8
cm.
(1)求证:△ABC为直角三角形;
(2)求AB边上的中线长.
(2)AB边上的中线长为4cm.
解:(1)∵∠B=
∠A=
∠C,
∴∠A=2∠B,∠C=3∠B.
∵∠A+∠B+∠C=2∠B+∠B+3∠B
=6∠B=180°,
∴∠B=30°,∠A=60°,∠C=90°
∴△ABC为直角三角形.
课堂小结
性质
判定
直角三角形两锐角互余.
直角三角形斜边上的中线等于斜边的一半.
有一个角为90°的三角形,叫做直角三角形.
有一个角是直角的三角形是直角三角形.
有两个角互余的三角形是直角三角形.
三角形一边上的中线等于这条边的一半的三角形
是直角三角形.
直角三角形
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
直角三角形的性质和判定
湘教版·八年级数学下册
上课课件
第一章
【知识与技能】
1.体验直角三角形应用的广泛性,理解直角三角形的定义,进一步认识直角三角形.
2.学会用符号和字母表示直角三角形.
3.经历“直角三角形两个锐角互余”的探讨,掌握直角三角形两个锐角互余的性质.
4.会用“两个锐角互余的三角形是直角三角形”这个判定方法判定直角三角形.
5.理解和掌握直角三角形性质“斜边上的中线等于斜边的一半”.
【过程与方法】
通过动手,猜想发现直角三角形的性质,引导逆向思维,探索性质的推导方法——同一法.
【情感态度】
体会从“一般到特殊”的思维方法和“逆向思维”方法,培养逆向思维能力.
【教学重点】
直角三角形性质和判定的探索及应用.
【教学难点】
直角三角形性质“斜边上的中线等于斜边的一半”的判定探索过程.
学习目标
复习导入
三角形定义
三
角
形
三角形性质
按边分类
按角分类
全等三角形
三角形分类
任意两边之和大于第三边
内角和定理及其推论
性质
判定(SAS、ASA、AAS、SSS)
锐角三角形
直角三角形
钝角三角形
性质
判定
等边三角形、等腰三角形
普通三角形
定义:有一个角是直角的三角形.
新课引入
如图1-1,在Rt△ABC中,∠C=90°,两锐角的和等于多少呢?
A
B
C
图1-1
解:在Rt△ABC中,∵∠C=90°,
由三角形内角和定理,
可得:∠A+∠B=90°.
由此得到:
直角三角形的两个锐角互余.
Rt△两锐角关系动态演示
几何画
板.gsp
随堂跟练
(1)如图(1),在△ABC中,∠ACB=90°,CD⊥AB于点D,若∠A=40°,则∠BCD=______.
(2)如图(2)在△ABC中,∠B=50°,高AD、CE交于H,则∠AHC=______.
40°
130°
A
C
D
B
(1)
A
C
B
D
H
E
(2)
有两个锐角互余的三角形是直角三角形吗?
A
B
C
图1-2
如图1-2,在△ABC中,∠A+∠B=90°,
那么△ABC是直角三角形吗?
解:在△ABC中,∵
∠A+∠B
+∠C=180°,
又∠A+∠B=90°,所以∠C=90°.
于是△ABC是直角三角形.
由此得到:
有两个角互余的三角形是直角三角形.
随堂跟练
(3)如图,AB∥CD,∠CAB和∠ACD的平分线相交于H点,那么△AHC是直角三角形吗?为什么?
A
B
C
D
H
解:∵AB//
CD,
∴∠
CAB+∠ACD=180°.
又∠CAH=
∠CAB,∠ACH=
∠ACD,
∴∠CAH+∠ACH
=
(∠CAB+∠ACD)=90°.
∴△AHC是直角三角形.
直角三角形的两个锐角互余.
直角三角形性质定理:
直角三角形判定定理:
有两个角互余的三角形是直角三角形.
互为逆命题
我测量后发现
探究新知
A
B
C
图1-3
如图1-3,画一个Rt△ABC,并作出斜边AB上的中线CD,比较线段CD与线段AB之间的数量关系,你能得出什么结论?
D
AB=
;
CD=
;
度量AB、CD的长度:
6cm
3cm
CD=
AB.
Rt△中线与斜边关系动态演示
几何画
板.gsp
探究新知
由此得到:
直角三角形斜边上的中线等于斜边的一半.
是否对于任意一个Rt△ABC,都有
?
CD=
AB
A
B
图1-4
D
C
E
F
证明:如图1-4,过点D作DE⊥AC,交AC于点E;作DF⊥BC,交BC于点F.
∵∠ACB=
∠AED=∠DFB
=
90°,
∴DE//
BC,DF//AC.
∴∠A=∠FDB,∠ADE=∠B.
又D为AB的中点,即AD=DB,
∴△AED≌△DFB
(ASA).
∴AE=DF,
DE=
BF.
同理可证△CDE≌△DCF,
从而DE=CF,CE=
DF.
∴AE=CE,BF=
CF.
故DE,
DF分别垂直平分边AC,
BC.
AD=CD=BD
(为什么?)
.
由此得到:CD=
AB
例
1
如图1-5,已知CD是△ABC的AB边上的中线,且CD=
AB.求证:△ABC是直角三角形.
A
B
图1-5
D
C
1
2
证明:∵CD=
AB=AD=BD,
∴∠1=∠A,∠2=∠B.
∵∠A+∠B+∠ACB=180°,
∠ACB=∠1+∠2
∴∠A+∠B
+∠1+∠2
=180°.
∴2(
∠A+∠B
)=180°.
∴∠A+∠B=90°.
∴△ABC是直角三角形.
(等边对等角)
(三角形内角和的性质)
(有两个角互余的三角形是直角三角形)
由此得到:___________________________________________________________
三角形一边上的中线等于这条边的一半的三角形是直角三角形.
直角三角形斜边上的中线等于斜边的一半.
三角形一边上的中线等于这条边的一半的三角形是直角三角形.
直角三角形性质定理:
直角三角形判定定理:
互为逆命题
巩固练习
1.在Rt△ABC中,斜边上的中线CD=2.5cm,则斜边AB的长是多少?
直角三角形斜边上的中线等于斜边的一半.
直角三角形性质定理:
AB=5cm
A
B
D
C
巩固练习
2.如图,AB∥CD,∠CAB和∠ACD的平分线相交于H点,E为AC的中点,EH=2.那么△AHC是直角三角形吗?为什么?若是,求出AC的长.
解:△AHC是直角三角形,理由:
∵AB∥CD,∴∠CAB+∠ACD=180°.
∵AH,CH分别为∠CAB,∠ACD的平分线,
∴∠CAH+∠ACH=90°.
∴∠AHC=90°,即△AHC是直角三角形.
∵E为AC的中点,∴AC=2EH=4.
巩固练习
1.如图,CD是Rt△ABC的中线,∠ACB=90°,
∠CDA
=120°,求∠B的度数.
解:∵CD是Rt△ABC斜边AB上的中线,
∴CD=DB=AD.
∵∠CDA=120°,
∴∠A=∠ACD=30°.
在Rt△ABC中,∠A+∠B=90°,∴∠B=60°.
巩固练习
2.如图,在△ABC中,已知∠B=
∠A=
∠C,AB=8
cm.
(1)求证:△ABC为直角三角形;
(2)求AB边上的中线长.
(2)AB边上的中线长为4cm.
解:(1)∵∠B=
∠A=
∠C,
∴∠A=2∠B,∠C=3∠B.
∵∠A+∠B+∠C=2∠B+∠B+3∠B
=6∠B=180°,
∴∠B=30°,∠A=60°,∠C=90°
∴△ABC为直角三角形.
课堂小结
性质
判定
直角三角形两锐角互余.
直角三角形斜边上的中线等于斜边的一半.
有一个角为90°的三角形,叫做直角三角形.
有一个角是直角的三角形是直角三角形.
有两个角互余的三角形是直角三角形.
三角形一边上的中线等于这条边的一半的三角形
是直角三角形.
直角三角形
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
