1.2 直角三角形的性质与判定(Ⅱ)(第1课时) 勾股定理 课件(共21张PPT)
文档属性
| 名称 | 1.2 直角三角形的性质与判定(Ⅱ)(第1课时) 勾股定理 课件(共21张PPT) |

|
|
| 格式 | rar | ||
| 文件大小 | 26.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 11:36:33 | ||
图片预览


文档简介
(共21张PPT)
勾股定理
湘教版·八年级数学下册
上课课件
第一章
学习目标
【知识与技能】
1.让学生体验勾股定理的探索过程.
2.掌握勾股定理.
3.学会用勾股定理解决简单的几何问题.
【过程与方法】
经历操作、归纳和猜想,用面积法推导作出肯定结论的过程,来了解勾股定理.
【情感态度】
了解我国古代数学家发现、推导和应用勾股定理中的贡献与成就,增进爱国主义情感,体验探索发现的过程和知识运用,增强学习数学的自信.
【教学重点】
勾股定理
【教学难点】
勾股定理的应用
情境导入
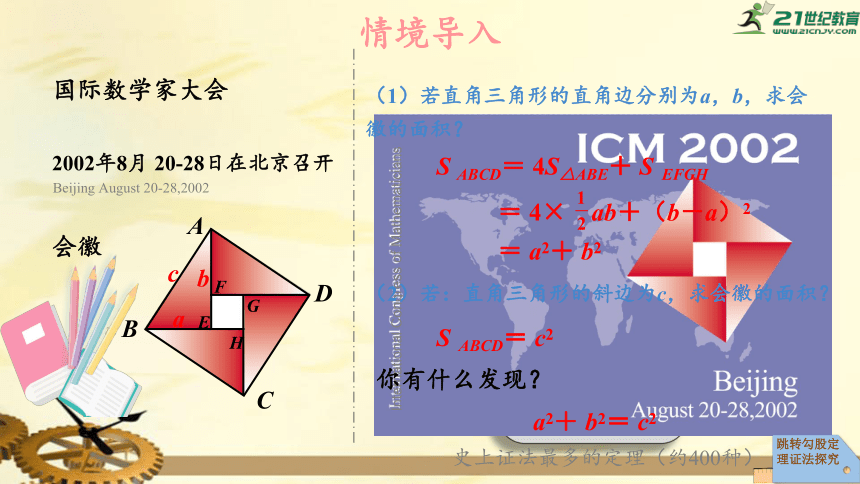
国际数学家大会
International
Congress
of
Mathematicians
2002年8月
20-28日在北京召开
Beijing
August
20-28,2002
会徽
(2)若:直角三角形的斜边为c,求会徽的面积?
(1)若直角三角形的直角边分别为a,b,求会徽的面积?
A
B
C
D
E
F
G
H
S
ABCD=
4S△ABE+
S
EFGH
=
a2+
b2
S
ABCD=
c2
=
4×
ab+(b-a)2
a
b
c
你有什么发现?
a2+
b2=
c2
史上证法最多的定理(约400种)
跳转勾股定理证法探究
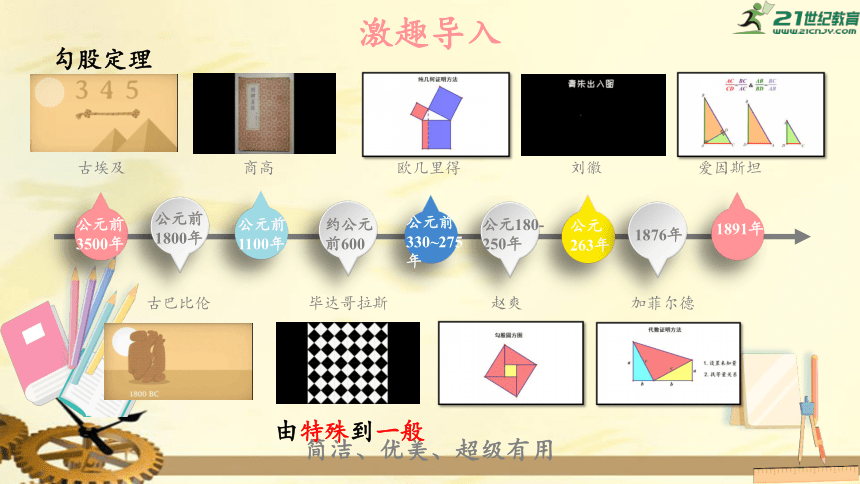
激趣导入
公元前3500年
毕达哥拉斯
赵爽
古埃及
欧几里得
商高
古巴比伦
公元前1100年
约公元前600
公元前330~275年
公元180-250年
公元前1800年
刘徽
公元263年
加菲尔德
1876年
1891年
爱因斯坦
勾股定理
简洁、优美、超级有用
由特殊到一般
毕达哥拉斯勾股定理证法特殊到一般背景介绍(时长1分50秒)
视频播放钮
勾股定理历史解说参考本
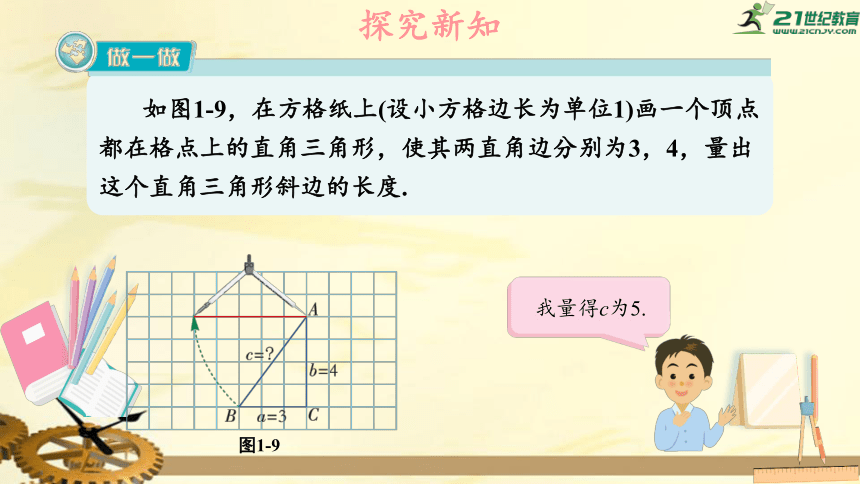
探究新知
如图1-9,在方格纸上(设小方格边长为单位1)画一个顶点都在格点上的直角三角形,使其两直角边分别为3,4,量出这个直角三角形斜边的长度.
图1-9
我量得c为5.
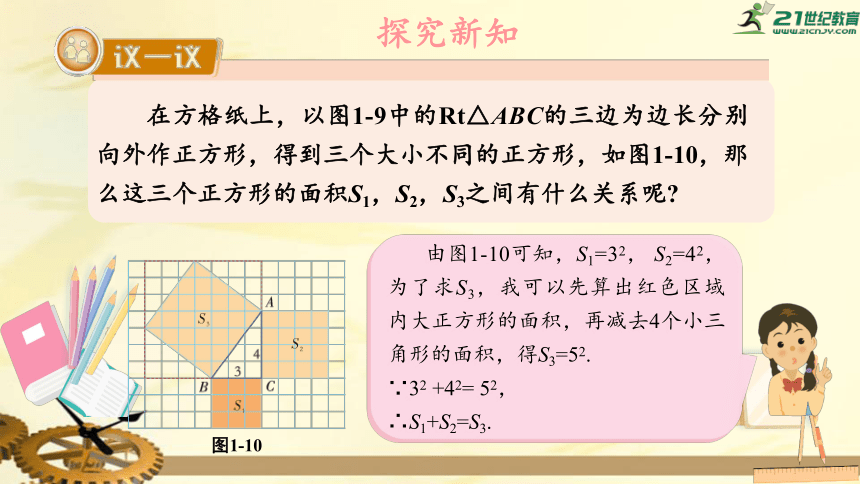
探究新知
在方格纸上,以图1-9中的Rt△ABC的三边为边长分别向外作正方形,得到三个大小不同的正方形,如图1-10,那么这三个正方形的面积S1,S2,S3之间有什么关系呢?
图1-10
由图1-10可知,S1=32,
S2=42,为了求S3,我可以先算出红色区域内大正方形的面积,再减去4个小三角形的面积,得S3=52.
∵32
+42=
52,
∴S1+S2=S3.
探究新知
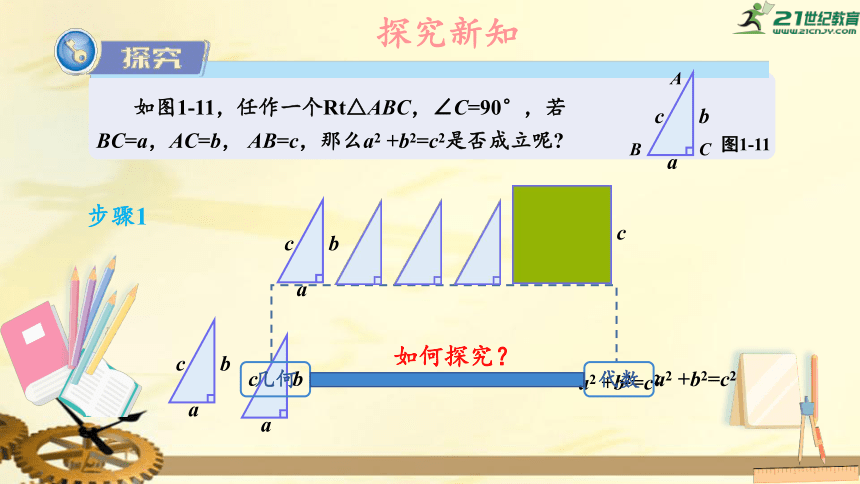
如图1-11,任作一个Rt△ABC,∠C=90°,若BC=a,AC=b,
AB=c,那么a2
+b2=c2是否成立呢?
A
B
C
图1-11
c
b
a
c
b
a
a2
+b2=c2
几何
代数
如何探究?
c
b
a
a2
+b2=c2
c
b
a
c
步骤1
教材P10页“探究”
PPT第2页赵爽
毕达哥拉斯法
探究新知
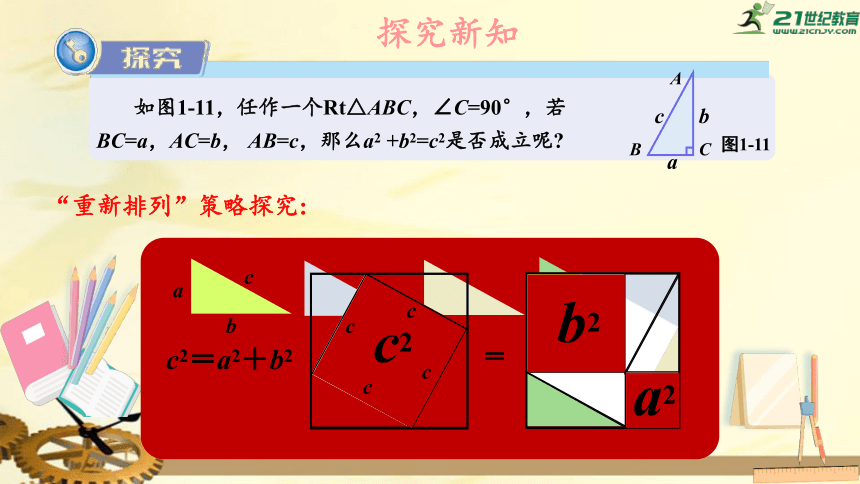
如图1-11,任作一个Rt△ABC,∠C=90°,若BC=a,AC=b,
AB=c,那么a2
+b2=c2是否成立呢?
①
A
B
C
图1-11
c
b
a
“重新排列”策略探究:
c
b
a
c2
b
b
a
a
=
c
c
c
c
c2
b2
a2
②
③
c2=a2+b2
(点击按钮③持续出动画)
探究新知
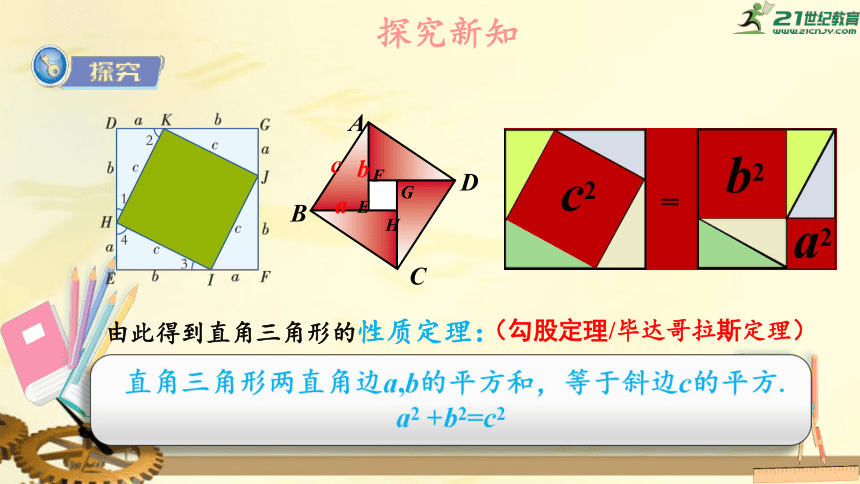
由此得到直角三角形的性质定理:
直角三角形两直角边a,b的平方和,等于斜边c的平方.
a2
+b2=c2
A
B
C
D
E
F
G
H
a
b
c
①
②
③
(勾股定理/毕达哥拉斯定理)
由此得到直角三角形的性质定理:
直角三角形两直角边a,b的平方和,等于斜边c的平方.
a2
+b2=c2
(勾股定理/毕达哥拉斯定理)
探究新知
变式:
a2=
c2-
b2,
b2=
c2-
a2
几何
代数
a2
+b2=c2
勾股定理
勾股定理反应了直角三角形三边的关系,成为沟通几何和代数的桥梁.
例
1
如图1-15,在等腰三角形ABC中,已知AB=AC=
13cm,BC=
10cm,AD⊥BC于点D.你能算出BC边上的高AD的长吗?
解:在△ABC中,
∵AB=AC=13,BC=10,AD⊥BC,
∴BD=
BC=5.
在Rt△ADB中,
由勾股定理得,AD2+BD2
=AB2,
故AD的长为12cm.
探究新知
【教材P11】
巩固练习
在Rt△ABC中,∠C=90°.
(1)已知a=25,b=15,求c;
(2)已知a=5,c=9,求b;
(3)已知b=5,c=15,求a.
解:根据勾股定理:
巩固练习
巩固练习
解:根据勾股定理:
答:AB长4.
巩固练习
作图演示
几何画
板.gsp
巩固练习
解:可得S1+S2=S3,
如果向外作半圆,则有
同理
即S1+S2=S3.
如果向外作等边三角形,则有
而a2+b2=c2.
即得S1+S2=S3.
课堂小结
直角三角形两直角边a,b的平方和,等于斜边c的平方.
a2
+b2=c2
勾股定理(毕达哥斯拉定理):
几何
代数
勾股定理
变式:
a2=
c2-
b2,
b2=
c2-
a2
直
角
三
角
形
性质
判定
直角三角形两锐角互余.
直角三角形斜边上的中线等于斜边的一半.
有一个角为90°的三角形,叫做直角三角形.
有一个角是直角的三角形是直角三角形.
有两个角互余的三角形是直角三角形.
三角形一边上的中线等于这条边的一半的三角形
是直角三角形.
勾股定理
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
勾股定理
湘教版·八年级数学下册
上课课件
第一章
学习目标
【知识与技能】
1.让学生体验勾股定理的探索过程.
2.掌握勾股定理.
3.学会用勾股定理解决简单的几何问题.
【过程与方法】
经历操作、归纳和猜想,用面积法推导作出肯定结论的过程,来了解勾股定理.
【情感态度】
了解我国古代数学家发现、推导和应用勾股定理中的贡献与成就,增进爱国主义情感,体验探索发现的过程和知识运用,增强学习数学的自信.
【教学重点】
勾股定理
【教学难点】
勾股定理的应用
情境导入
国际数学家大会
International
Congress
of
Mathematicians
2002年8月
20-28日在北京召开
Beijing
August
20-28,2002
会徽
(2)若:直角三角形的斜边为c,求会徽的面积?
(1)若直角三角形的直角边分别为a,b,求会徽的面积?
A
B
C
D
E
F
G
H
S
ABCD=
4S△ABE+
S
EFGH
=
a2+
b2
S
ABCD=
c2
=
4×
ab+(b-a)2
a
b
c
你有什么发现?
a2+
b2=
c2
史上证法最多的定理(约400种)
跳转勾股定理证法探究
激趣导入
公元前3500年
毕达哥拉斯
赵爽
古埃及
欧几里得
商高
古巴比伦
公元前1100年
约公元前600
公元前330~275年
公元180-250年
公元前1800年
刘徽
公元263年
加菲尔德
1876年
1891年
爱因斯坦
勾股定理
简洁、优美、超级有用
由特殊到一般
毕达哥拉斯勾股定理证法特殊到一般背景介绍(时长1分50秒)
视频播放钮
勾股定理历史解说参考本
探究新知
如图1-9,在方格纸上(设小方格边长为单位1)画一个顶点都在格点上的直角三角形,使其两直角边分别为3,4,量出这个直角三角形斜边的长度.
图1-9
我量得c为5.
探究新知
在方格纸上,以图1-9中的Rt△ABC的三边为边长分别向外作正方形,得到三个大小不同的正方形,如图1-10,那么这三个正方形的面积S1,S2,S3之间有什么关系呢?
图1-10
由图1-10可知,S1=32,
S2=42,为了求S3,我可以先算出红色区域内大正方形的面积,再减去4个小三角形的面积,得S3=52.
∵32
+42=
52,
∴S1+S2=S3.
探究新知
如图1-11,任作一个Rt△ABC,∠C=90°,若BC=a,AC=b,
AB=c,那么a2
+b2=c2是否成立呢?
A
B
C
图1-11
c
b
a
c
b
a
a2
+b2=c2
几何
代数
如何探究?
c
b
a
a2
+b2=c2
c
b
a
c
步骤1
教材P10页“探究”
PPT第2页赵爽
毕达哥拉斯法
探究新知
如图1-11,任作一个Rt△ABC,∠C=90°,若BC=a,AC=b,
AB=c,那么a2
+b2=c2是否成立呢?
①
A
B
C
图1-11
c
b
a
“重新排列”策略探究:
c
b
a
c2
b
b
a
a
=
c
c
c
c
c2
b2
a2
②
③
c2=a2+b2
(点击按钮③持续出动画)
探究新知
由此得到直角三角形的性质定理:
直角三角形两直角边a,b的平方和,等于斜边c的平方.
a2
+b2=c2
A
B
C
D
E
F
G
H
a
b
c
①
②
③
(勾股定理/毕达哥拉斯定理)
由此得到直角三角形的性质定理:
直角三角形两直角边a,b的平方和,等于斜边c的平方.
a2
+b2=c2
(勾股定理/毕达哥拉斯定理)
探究新知
变式:
a2=
c2-
b2,
b2=
c2-
a2
几何
代数
a2
+b2=c2
勾股定理
勾股定理反应了直角三角形三边的关系,成为沟通几何和代数的桥梁.
例
1
如图1-15,在等腰三角形ABC中,已知AB=AC=
13cm,BC=
10cm,AD⊥BC于点D.你能算出BC边上的高AD的长吗?
解:在△ABC中,
∵AB=AC=13,BC=10,AD⊥BC,
∴BD=
BC=5.
在Rt△ADB中,
由勾股定理得,AD2+BD2
=AB2,
故AD的长为12cm.
探究新知
【教材P11】
巩固练习
在Rt△ABC中,∠C=90°.
(1)已知a=25,b=15,求c;
(2)已知a=5,c=9,求b;
(3)已知b=5,c=15,求a.
解:根据勾股定理:
巩固练习
巩固练习
解:根据勾股定理:
答:AB长4.
巩固练习
作图演示
几何画
板.gsp
巩固练习
解:可得S1+S2=S3,
如果向外作半圆,则有
同理
即S1+S2=S3.
如果向外作等边三角形,则有
而a2+b2=c2.
即得S1+S2=S3.
课堂小结
直角三角形两直角边a,b的平方和,等于斜边c的平方.
a2
+b2=c2
勾股定理(毕达哥斯拉定理):
几何
代数
勾股定理
变式:
a2=
c2-
b2,
b2=
c2-
a2
直
角
三
角
形
性质
判定
直角三角形两锐角互余.
直角三角形斜边上的中线等于斜边的一半.
有一个角为90°的三角形,叫做直角三角形.
有一个角是直角的三角形是直角三角形.
有两个角互余的三角形是直角三角形.
三角形一边上的中线等于这条边的一半的三角形
是直角三角形.
勾股定理
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
