人教版数学四年级下册7.2 平移 解决问题 例4 课件(24张ppt)
文档属性
| 名称 | 人教版数学四年级下册7.2 平移 解决问题 例4 课件(24张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 14:31:43 | ||
图片预览


文档简介
(共23张PPT)
解决问题例4
人教版数学 四年级下册 第七单元
1. 运用平移的方法将简单不规则图形转化成规则图形
并正确解决面积问题,加深对平移这种图形变换方式的理解。
2. 在解决简单不规则图形面积问题的过程中,渗透变换的数学思想,培养迁移、转化的能力,发展空间观念。
3. 在变与不变中体验化难为易的思想价值,体会数学
知识间的密切联系,感受数学美。
学 习 目 标
1cm
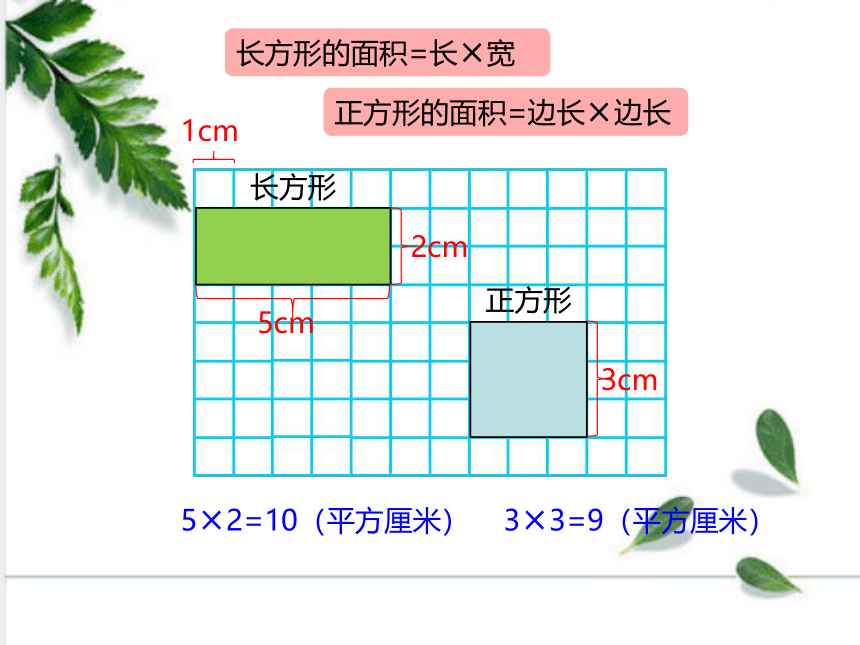
长方形的面积=长×宽
正方形的面积=边长×边长
5×2=10(平方厘米)
3×3=9(平方厘米)
5cm
2cm
3cm
长方形
正方形
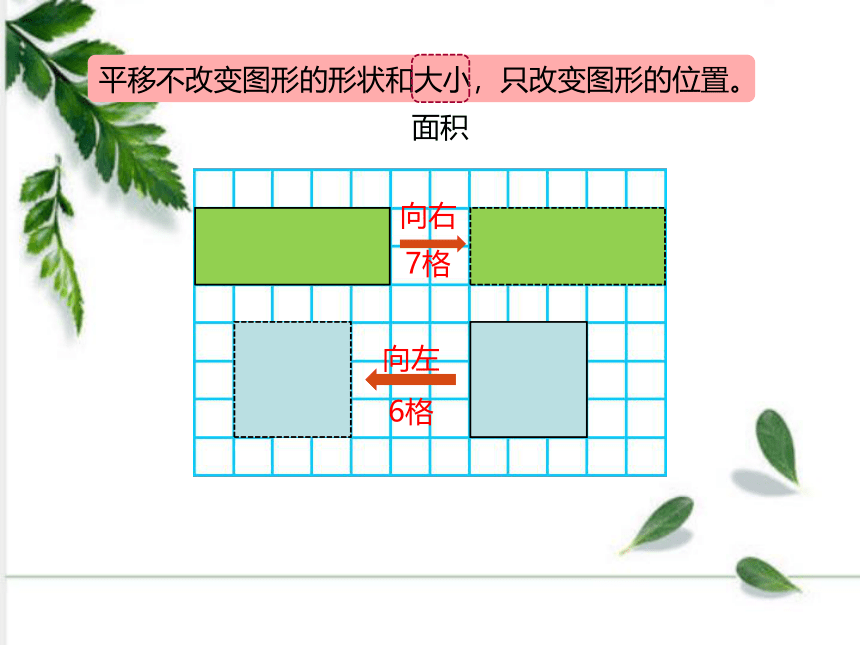
7格
平移不改变图形的形状和大小,只改变图形的位置。
向右
向左
6格
面积
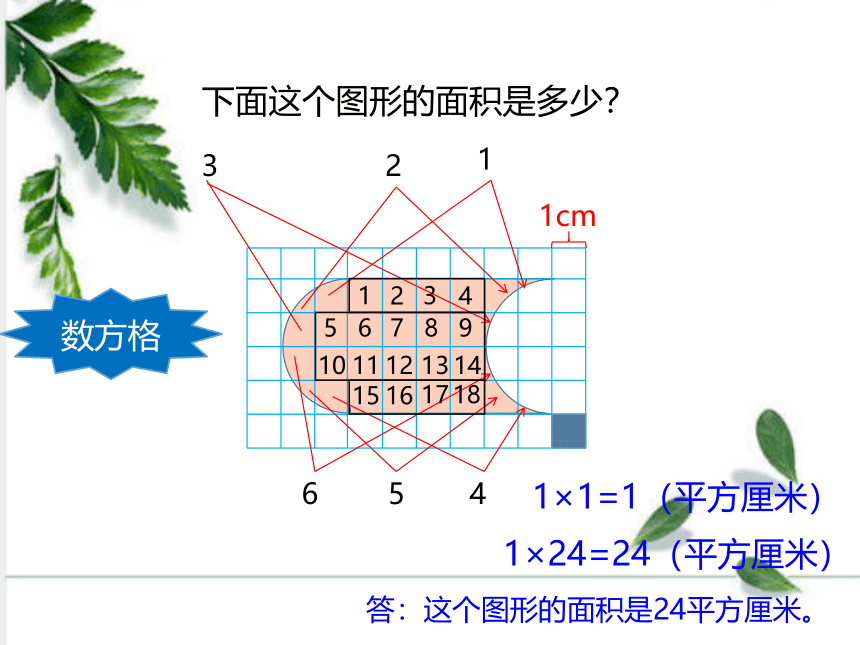
下面这个图形的面积是多少?
数方格
1cm
1
2
3
4
5
6
1×24=24(平方厘米)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
1×1=1(平方厘米)
答:这个图形的面积是24平方厘米。
1cm
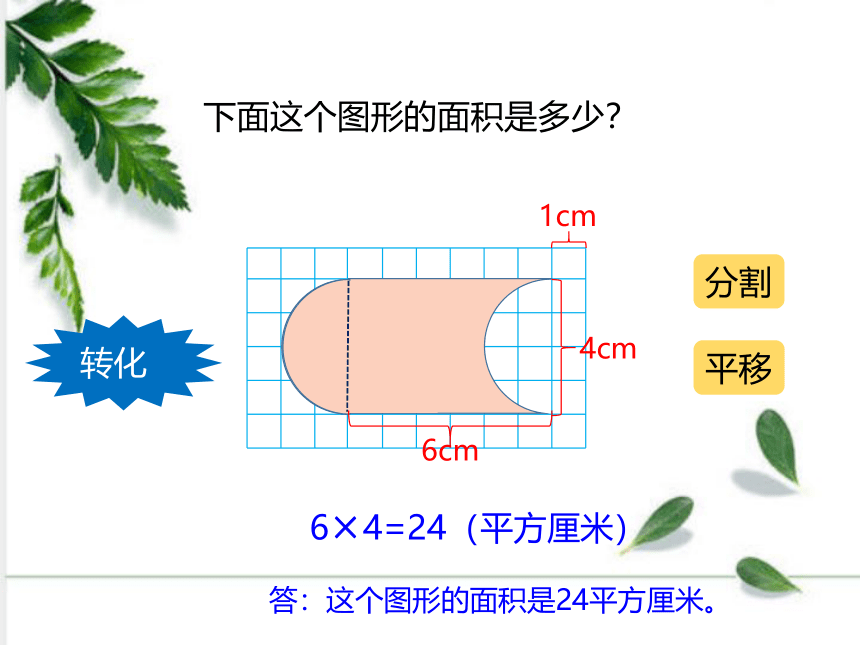
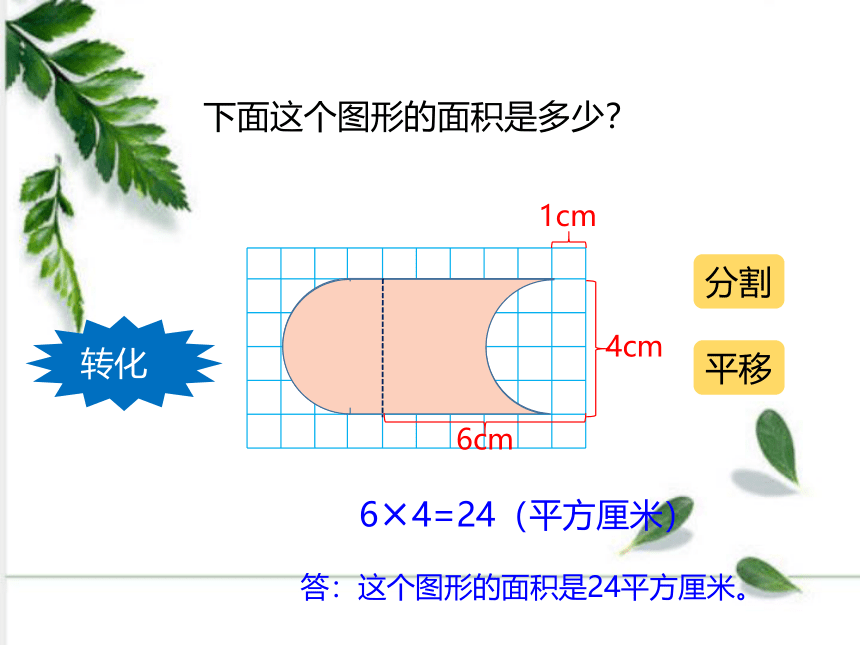
下面这个图形的面积是多少?
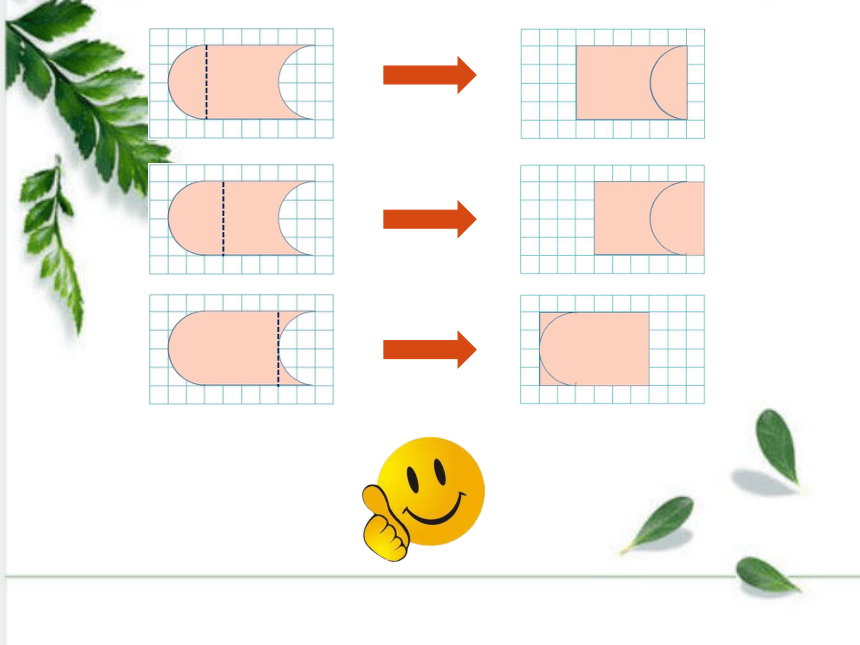
转化
分割
平移
6×4=24(平方厘米)
6cm
4cm
答:这个图形的面积是24平方厘米。
1cm
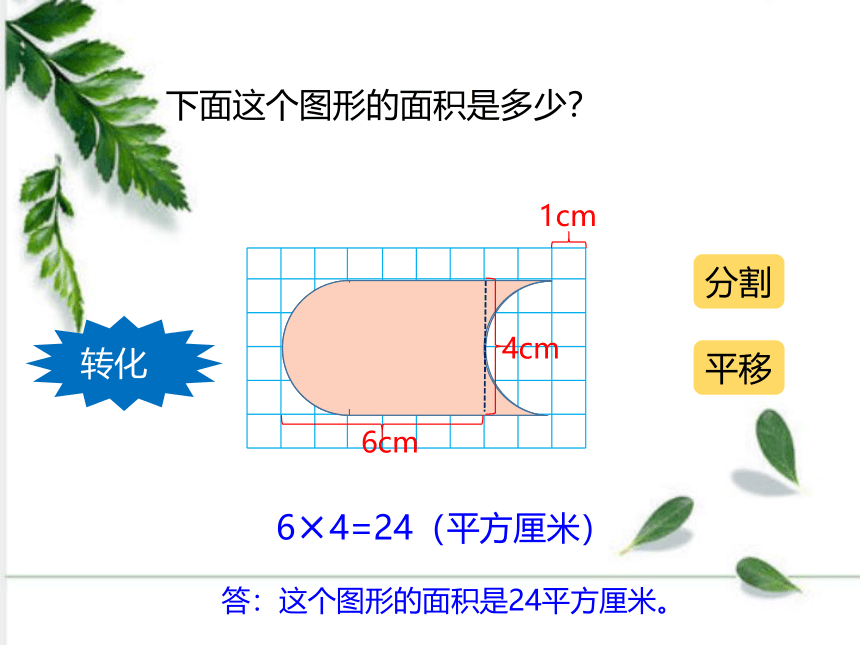
下面这个图形的面积是多少?
转化
分割
平移
6×4=24(平方厘米)
6cm
4cm
答:这个图形的面积是24平方厘米。
1cm
下面这个图形的面积是多少?
转化
分割
平移
6×4=24(平方厘米)
6cm
4cm
答:这个图形的面积是24平方厘米。
1cm
下面这个图形的面积是多少?
转化
分割
6×4=24(平方厘米)
平移
4cm
6cm
不规则图形
面积不变
平移
转化
规则图形
割补法
割 补 法
割补法是计算平面几何图形面积的推导方法,也是一种思考方法。在面积和体积学习中,都有着广泛的应用。
割补法是指:把一个图形的某一部分割下来,填补在图形的另一部分,在原来面积不变的情况下,使其转化为已经掌握的旧的图形,以利于计算公式的推导和运用。平行四边形通过割补可转化为长方形(或正方形),梯形通过割补可转化为平行四边形,圆通过割补可转化为近似长方形等等。
刘徽
出入相补原理指的是一个平面图形从一处移到他处,面积保持不变;又若把图形分割成若干部分,则各部分面积之间等于原图形的面积,因而图形移置前后诸面积间的和、差有简单的相等关系。
出入相补
1. 涂色部分占整个图形的几分之几?
(课本第88页第3题)
( )
( )
( )
( )
( )
( )
1
3
1
2
1
3
2. 画一画,量一量,算出下面这个火箭的面积。
(课本第87页做一做)
9厘米
3厘米
9×3=27(平方厘米)
答:这个火箭的面积是27平方厘米。
3. 计算这个风车的面积。
4×2=8(平方米)
答:这个风车的面积是8平方米。
1m
4m
2m
14m
4. 在一个长30m,宽14m的长方形草坪上有两条宽1m的小路
相交,那么草坪的面积是多少平方米?
30m
1m
1m
1m
1m
( )× ( )
答:草坪的面积是377平方米。
30 1
14 1
= 29× 13
= 377(平方米 )
算出下面图形的周长。
(10+7)×2
1cm
= 17×2
= 34(厘米)
10cm
7cm
答:这个图形的周长是34厘米。
求这个图形的周长和面积。
(5+4)×2
.
1cm
答:这个图形的周长是18cm。
5cm
4cm
=9×2
=18(cm)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
(5+2)×2
求这个图形的周长和面积。
1cm
答:这个图形的面积是14cm 。
7cm
2cm
=7×2
=14(cm )
1. 运用平移的方法将简单不规则图形转化成规则图形
并正确解决面积问题,加深对平移这种图形变换方式的理解。
2. 在解决简单不规则图形面积问题的过程中,渗透变换的数学思想,培养迁移、转化的能力,发展空间观念。
3. 在变与不变中体验化难为易的思想价值,体会数学
知识间的密切联系,感受数学美。
学 习 目 标
不规则图形
面积不变
周长不变
平移
转化
规则图形
平移不改变图形的形状和大小,只改变图形的位置。
祝同学们学习愉快
解决问题例4
人教版数学 四年级下册 第七单元
1. 运用平移的方法将简单不规则图形转化成规则图形
并正确解决面积问题,加深对平移这种图形变换方式的理解。
2. 在解决简单不规则图形面积问题的过程中,渗透变换的数学思想,培养迁移、转化的能力,发展空间观念。
3. 在变与不变中体验化难为易的思想价值,体会数学
知识间的密切联系,感受数学美。
学 习 目 标
1cm
长方形的面积=长×宽
正方形的面积=边长×边长
5×2=10(平方厘米)
3×3=9(平方厘米)
5cm
2cm
3cm
长方形
正方形
7格
平移不改变图形的形状和大小,只改变图形的位置。
向右
向左
6格
面积
下面这个图形的面积是多少?
数方格
1cm
1
2
3
4
5
6
1×24=24(平方厘米)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
1×1=1(平方厘米)
答:这个图形的面积是24平方厘米。
1cm
下面这个图形的面积是多少?
转化
分割
平移
6×4=24(平方厘米)
6cm
4cm
答:这个图形的面积是24平方厘米。
1cm
下面这个图形的面积是多少?
转化
分割
平移
6×4=24(平方厘米)
6cm
4cm
答:这个图形的面积是24平方厘米。
1cm
下面这个图形的面积是多少?
转化
分割
平移
6×4=24(平方厘米)
6cm
4cm
答:这个图形的面积是24平方厘米。
1cm
下面这个图形的面积是多少?
转化
分割
6×4=24(平方厘米)
平移
4cm
6cm
不规则图形
面积不变
平移
转化
规则图形
割补法
割 补 法
割补法是计算平面几何图形面积的推导方法,也是一种思考方法。在面积和体积学习中,都有着广泛的应用。
割补法是指:把一个图形的某一部分割下来,填补在图形的另一部分,在原来面积不变的情况下,使其转化为已经掌握的旧的图形,以利于计算公式的推导和运用。平行四边形通过割补可转化为长方形(或正方形),梯形通过割补可转化为平行四边形,圆通过割补可转化为近似长方形等等。
刘徽
出入相补原理指的是一个平面图形从一处移到他处,面积保持不变;又若把图形分割成若干部分,则各部分面积之间等于原图形的面积,因而图形移置前后诸面积间的和、差有简单的相等关系。
出入相补
1. 涂色部分占整个图形的几分之几?
(课本第88页第3题)
( )
( )
( )
( )
( )
( )
1
3
1
2
1
3
2. 画一画,量一量,算出下面这个火箭的面积。
(课本第87页做一做)
9厘米
3厘米
9×3=27(平方厘米)
答:这个火箭的面积是27平方厘米。
3. 计算这个风车的面积。
4×2=8(平方米)
答:这个风车的面积是8平方米。
1m
4m
2m
14m
4. 在一个长30m,宽14m的长方形草坪上有两条宽1m的小路
相交,那么草坪的面积是多少平方米?
30m
1m
1m
1m
1m
( )× ( )
答:草坪的面积是377平方米。
30 1
14 1
= 29× 13
= 377(平方米 )
算出下面图形的周长。
(10+7)×2
1cm
= 17×2
= 34(厘米)
10cm
7cm
答:这个图形的周长是34厘米。
求这个图形的周长和面积。
(5+4)×2
.
1cm
答:这个图形的周长是18cm。
5cm
4cm
=9×2
=18(cm)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
(5+2)×2
求这个图形的周长和面积。
1cm
答:这个图形的面积是14cm 。
7cm
2cm
=7×2
=14(cm )
1. 运用平移的方法将简单不规则图形转化成规则图形
并正确解决面积问题,加深对平移这种图形变换方式的理解。
2. 在解决简单不规则图形面积问题的过程中,渗透变换的数学思想,培养迁移、转化的能力,发展空间观念。
3. 在变与不变中体验化难为易的思想价值,体会数学
知识间的密切联系,感受数学美。
学 习 目 标
不规则图形
面积不变
周长不变
平移
转化
规则图形
平移不改变图形的形状和大小,只改变图形的位置。
祝同学们学习愉快
