1.3 二元一次方程组的应用(第1课时) 用二元一次方程组解决较为简单的实际问题 课件(共17张PPT)
文档属性
| 名称 | 1.3 二元一次方程组的应用(第1课时) 用二元一次方程组解决较为简单的实际问题 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 13:27:21 | ||
图片预览





文档简介
(共17张PPT)
用二元一次方程组解决较为简单的实际问题
湘教版·七年级数学下册
上课课件
第1章
二元一次方程组
学习目标
【知识与技能】
1.通过实际问题使学生感受二元一次方程组的广泛应用,体会列二元一次方程组是解决某些实际问题的一种有效的数学模型,增强应用意识;
2.能够由题意找出等量关系,列出二元一次方程组并检验所得结果是否符合实际意义.
【过程与方法】
教师引导学生的自主探索,体会把实际问题转化到数学方程问题的数学思想方法,加强知识的综合运用,培养学生分析问题和解决问题的能力.
【情感态度】
使学生体验数学活动充满探索与创造,体会到经济社会中数学的应用价值,提高学生探索的精神与能力.
【教学重点】
把应用问题转化为数学问题的过程,即对实际问题的数学模型的建立.
【教学难点】
在实践探索中寻找解题方案.
情境导入
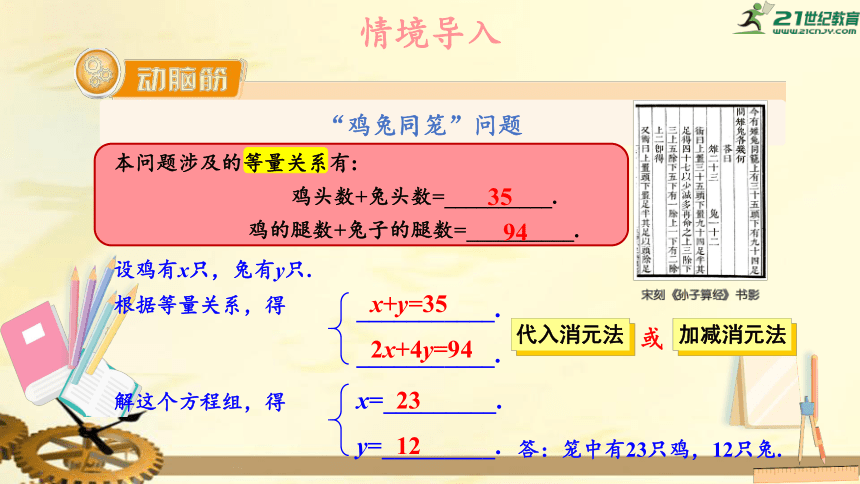
本问题涉及的等量关系有:
鸡头数+兔头数=__________.
鸡的腿数+兔子的腿数=__________.
35
94
本问题涉及的等量关系有:
鸡头数+兔头数=__________.
鸡的腿数+兔子的腿数=__________.
35
94
情境导入
“鸡兔同笼”问题
设鸡有x只,兔有y只.
根据等量关系,得
___________.
___________.
x+y=35
2x+4y=94
解这个方程组,得
x=_________.
y=_________.
23
12
答:笼中有23只鸡,12只兔.
代入消元法
加减消元法
或
设两个未知数
探究新知
例
1
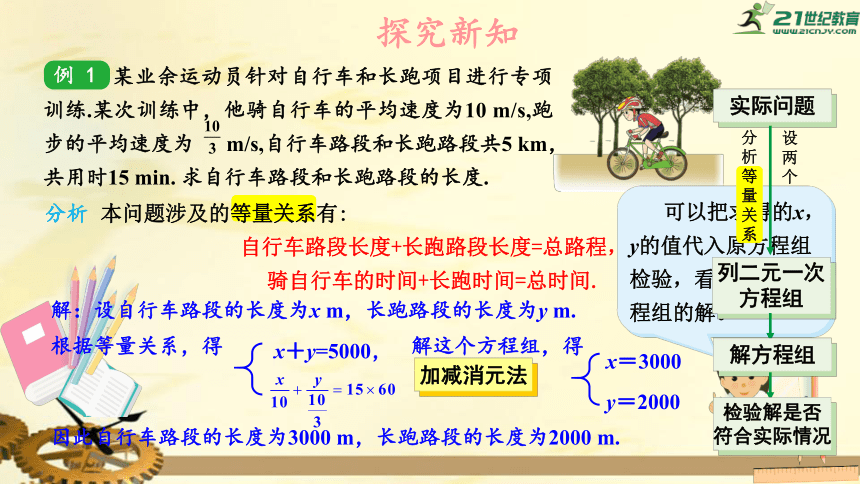
某业余运动员针对自行车和长跑项目进行专项训练.某次训练中,他骑自行车的平均速度为10
m/s,跑步的平均速度为
m/s,自行车路段和长跑路段共5
km,共用时15
min.
求自行车路段和长跑路段的长度.
本问题涉及的等量关系有:
自行车路段长度+长跑路段长度=总路程,
骑自行车的时间+长跑时间=总时间.
分析
解:设自行车路段的长度为x
m,长跑路段的长度为y
m.
根据等量关系,得
x+y=5000,
解这个方程组,得
x=3000
y=2000
因此自行车路段的长度为3000
m,长跑路段的长度为2000
m.
可以把求得的x,y的值代入原方程组检验,看是否为方程组的解。
加减消元法
实际问题
列二元一次
方程组
解方程组
检验解是否
符合实际情况
分析等量关系
探究新知
某食品厂要配制含蛋白质15%的食品100kg,现在有含蛋白质分别为20%,12%的甲乙两种配料.用这两种配料可以配制出所要求的食品吗?如果可以的话,它们各需多少千克?
本问题涉及的等量关系有:
甲配料质量+乙配料质量=总质量,
甲配料含蛋白质质量+乙配料含蛋白质质量=总蛋白质质量.
分析
解:设含蛋白质20%的配料需用x
kg,含蛋白质12%的配料需用y
kg..
根据等量关系,得
x+y=100,
x·20%+y·12%=100·15%,
解这个方程组,得
x=37.5
y=62.5
答:可以配制出所要求的食品,其中含蛋白质20%的配料需用37.5
kg,含蛋白质12%的配料需用62.5
kg.
代入消元法
设两个未知数
实际问题
列二元一次
方程组
解方程组
检验解是否
符合实际情况
分析等量关系
例
2
巩固练习
解:设合金中含金xg,含银y
g,则
x+y=250,
解得
x=190,
y=60.
答:合金中含金190g,含银60g.
本问题涉及的等量关系有:
金的重量+银的重量=总重量,
金在水中减去重量+银在水中减去重量=合金在水中减去的总重量.
分析
1.一块金与银的合金重250g,放在水中称,减轻了16g.已知金在水中称,金重减轻
;银在水中称,银重减轻
.求这块合金中含金、银各多少克.
巩固练习
解:设甲、乙两种商品原来的单价分别为x元,y元,则
x+y=100,
90%x+140%y=120%(x+y),
解得
x=40,
y=60.
答:甲、乙两种商品原来的单价分别为40元、60元.
本问题涉及的等量关系有:
甲的单价+乙的单价=100元,
(1-10%)甲的单价+(1+40%)乙的单价=(1+20%)×100元.
分析
2.甲、乙两种商品原来的单价和为100元,因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了。20%.
求甲、乙两
种商品原来的单价.
巩固练习
1.小红买了80分与60分的邮票共17枚,花去12.2元.试问:80分与60分邮票各买了多少枚?
解:设80分与60分的邮票分别买了x枚,y枚,则
x+y=17,
0.8x+0.6y=12.2,
解得
x=10,
y=7.
答:80分与60分的邮票各买了10枚、7枚.
本问题涉及的等量关系有:
80分邮票数量+60分邮票数量=17枚,
80分邮票总价钱+60分邮票总价钱=12.2元.
分析
巩固练习
2.小亮对小芬说:“我的生日的月和日相加是37,月的2倍和日相加是43.”
小芬说:“这不可能啊!”
你觉得小芬说得对吗?为什么?
答:对,因为小亮所说的是6月31日,这是不可能的.
本问题涉及的等量关系有:
月+日=37,
月×2+日=43.
分析
解:设月、日分别是x,y,则
x+y=37,
2x+y=43,
x=6,
y=31.
解得
3.小英家今年1月份用水20t,交水费43元;2月份用水18t,交水费38元.该城市实行阶梯水价,14
t以内按正常收费,超出部分则收较高水费.问:在限定量以内的水费每吨多少元?超出部分的水费每吨多少元?
巩固练习
解:设在限定量以内的水费每吨x元,超出部分的水费每吨y元,则
14x+6y=43,
14x+4y=38,
解得
x=2,
y=2.5.
答:在限定量以内的水费每吨2元,超出部分的水费每吨2.5元.
本问题涉及的等量关系有:
1月份14
t以内的水费+1月份超出水费=43元,
2月份14
t以内的水费+2月份超出水费=38元.
分析
4.某企业向商业银行申请了甲、乙两种贷款,共计35万元,每年需付出利息4.4万元.甲种贷款每年的利率是12%,乙种贷款的利率是13%.求这两种贷款的金额各是多少.
解:设在甲种贷款x万元,乙种贷款y万元,则
x+y=35,
12%x+13%y=4.4,
解得
x=15,
y=20.
答:甲种贷款15万元,乙种贷款20万元.
巩固练习
本问题涉及的等量关系有:
甲种贷款+乙种贷款=35万元,
甲种贷款年利率+乙种贷款年利率=4.4万元.
分析
5.某水果公司收购某种水果104
t,准备加工后上市销售.该公司加工该种水果的能力是:每天可以精加工4t或粗加工8t.现水果公司计划用16天完成这项加工任务,则应安排几天精加工,几天粗加工?
巩固练习
解:设应安排x天精加工,y天粗加工,则
x+y=16,
4x+8y=104,
解得
x=6,
y=10.
答:应安排6天精加工,10天粗加工.
本问题涉及的等量关系有:
精加工天数+粗加工天数=总天数,
精加工天数×4t+粗加工天数×8t=水果总量.
分析
课堂小结
建立二元一次方程组解决实际问题的步骤如下:
设两个未知数
实际问题
列二元一次
方程组
解方程组
检验解是否
符合实际情况
分析等量关系
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
用二元一次方程组解决较为简单的实际问题
湘教版·七年级数学下册
上课课件
第1章
二元一次方程组
学习目标
【知识与技能】
1.通过实际问题使学生感受二元一次方程组的广泛应用,体会列二元一次方程组是解决某些实际问题的一种有效的数学模型,增强应用意识;
2.能够由题意找出等量关系,列出二元一次方程组并检验所得结果是否符合实际意义.
【过程与方法】
教师引导学生的自主探索,体会把实际问题转化到数学方程问题的数学思想方法,加强知识的综合运用,培养学生分析问题和解决问题的能力.
【情感态度】
使学生体验数学活动充满探索与创造,体会到经济社会中数学的应用价值,提高学生探索的精神与能力.
【教学重点】
把应用问题转化为数学问题的过程,即对实际问题的数学模型的建立.
【教学难点】
在实践探索中寻找解题方案.
情境导入
本问题涉及的等量关系有:
鸡头数+兔头数=__________.
鸡的腿数+兔子的腿数=__________.
35
94
本问题涉及的等量关系有:
鸡头数+兔头数=__________.
鸡的腿数+兔子的腿数=__________.
35
94
情境导入
“鸡兔同笼”问题
设鸡有x只,兔有y只.
根据等量关系,得
___________.
___________.
x+y=35
2x+4y=94
解这个方程组,得
x=_________.
y=_________.
23
12
答:笼中有23只鸡,12只兔.
代入消元法
加减消元法
或
设两个未知数
探究新知
例
1
某业余运动员针对自行车和长跑项目进行专项训练.某次训练中,他骑自行车的平均速度为10
m/s,跑步的平均速度为
m/s,自行车路段和长跑路段共5
km,共用时15
min.
求自行车路段和长跑路段的长度.
本问题涉及的等量关系有:
自行车路段长度+长跑路段长度=总路程,
骑自行车的时间+长跑时间=总时间.
分析
解:设自行车路段的长度为x
m,长跑路段的长度为y
m.
根据等量关系,得
x+y=5000,
解这个方程组,得
x=3000
y=2000
因此自行车路段的长度为3000
m,长跑路段的长度为2000
m.
可以把求得的x,y的值代入原方程组检验,看是否为方程组的解。
加减消元法
实际问题
列二元一次
方程组
解方程组
检验解是否
符合实际情况
分析等量关系
探究新知
某食品厂要配制含蛋白质15%的食品100kg,现在有含蛋白质分别为20%,12%的甲乙两种配料.用这两种配料可以配制出所要求的食品吗?如果可以的话,它们各需多少千克?
本问题涉及的等量关系有:
甲配料质量+乙配料质量=总质量,
甲配料含蛋白质质量+乙配料含蛋白质质量=总蛋白质质量.
分析
解:设含蛋白质20%的配料需用x
kg,含蛋白质12%的配料需用y
kg..
根据等量关系,得
x+y=100,
x·20%+y·12%=100·15%,
解这个方程组,得
x=37.5
y=62.5
答:可以配制出所要求的食品,其中含蛋白质20%的配料需用37.5
kg,含蛋白质12%的配料需用62.5
kg.
代入消元法
设两个未知数
实际问题
列二元一次
方程组
解方程组
检验解是否
符合实际情况
分析等量关系
例
2
巩固练习
解:设合金中含金xg,含银y
g,则
x+y=250,
解得
x=190,
y=60.
答:合金中含金190g,含银60g.
本问题涉及的等量关系有:
金的重量+银的重量=总重量,
金在水中减去重量+银在水中减去重量=合金在水中减去的总重量.
分析
1.一块金与银的合金重250g,放在水中称,减轻了16g.已知金在水中称,金重减轻
;银在水中称,银重减轻
.求这块合金中含金、银各多少克.
巩固练习
解:设甲、乙两种商品原来的单价分别为x元,y元,则
x+y=100,
90%x+140%y=120%(x+y),
解得
x=40,
y=60.
答:甲、乙两种商品原来的单价分别为40元、60元.
本问题涉及的等量关系有:
甲的单价+乙的单价=100元,
(1-10%)甲的单价+(1+40%)乙的单价=(1+20%)×100元.
分析
2.甲、乙两种商品原来的单价和为100元,因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了。20%.
求甲、乙两
种商品原来的单价.
巩固练习
1.小红买了80分与60分的邮票共17枚,花去12.2元.试问:80分与60分邮票各买了多少枚?
解:设80分与60分的邮票分别买了x枚,y枚,则
x+y=17,
0.8x+0.6y=12.2,
解得
x=10,
y=7.
答:80分与60分的邮票各买了10枚、7枚.
本问题涉及的等量关系有:
80分邮票数量+60分邮票数量=17枚,
80分邮票总价钱+60分邮票总价钱=12.2元.
分析
巩固练习
2.小亮对小芬说:“我的生日的月和日相加是37,月的2倍和日相加是43.”
小芬说:“这不可能啊!”
你觉得小芬说得对吗?为什么?
答:对,因为小亮所说的是6月31日,这是不可能的.
本问题涉及的等量关系有:
月+日=37,
月×2+日=43.
分析
解:设月、日分别是x,y,则
x+y=37,
2x+y=43,
x=6,
y=31.
解得
3.小英家今年1月份用水20t,交水费43元;2月份用水18t,交水费38元.该城市实行阶梯水价,14
t以内按正常收费,超出部分则收较高水费.问:在限定量以内的水费每吨多少元?超出部分的水费每吨多少元?
巩固练习
解:设在限定量以内的水费每吨x元,超出部分的水费每吨y元,则
14x+6y=43,
14x+4y=38,
解得
x=2,
y=2.5.
答:在限定量以内的水费每吨2元,超出部分的水费每吨2.5元.
本问题涉及的等量关系有:
1月份14
t以内的水费+1月份超出水费=43元,
2月份14
t以内的水费+2月份超出水费=38元.
分析
4.某企业向商业银行申请了甲、乙两种贷款,共计35万元,每年需付出利息4.4万元.甲种贷款每年的利率是12%,乙种贷款的利率是13%.求这两种贷款的金额各是多少.
解:设在甲种贷款x万元,乙种贷款y万元,则
x+y=35,
12%x+13%y=4.4,
解得
x=15,
y=20.
答:甲种贷款15万元,乙种贷款20万元.
巩固练习
本问题涉及的等量关系有:
甲种贷款+乙种贷款=35万元,
甲种贷款年利率+乙种贷款年利率=4.4万元.
分析
5.某水果公司收购某种水果104
t,准备加工后上市销售.该公司加工该种水果的能力是:每天可以精加工4t或粗加工8t.现水果公司计划用16天完成这项加工任务,则应安排几天精加工,几天粗加工?
巩固练习
解:设应安排x天精加工,y天粗加工,则
x+y=16,
4x+8y=104,
解得
x=6,
y=10.
答:应安排6天精加工,10天粗加工.
本问题涉及的等量关系有:
精加工天数+粗加工天数=总天数,
精加工天数×4t+粗加工天数×8t=水果总量.
分析
课堂小结
建立二元一次方程组解决实际问题的步骤如下:
设两个未知数
实际问题
列二元一次
方程组
解方程组
检验解是否
符合实际情况
分析等量关系
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
