1.3 直角三角形全等的判定 练习课(习题1.3) 习题课件(共11张PPT)
文档属性
| 名称 | 1.3 直角三角形全等的判定 练习课(习题1.3) 习题课件(共11张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 00:00:00 | ||
图片预览


文档简介
(共11张PPT)
练习课
第1章
直角三角形
湘教版·八年级数学下册
上课课件
1.如图,AB=AD,CB⊥AB于点B,CD⊥AD于点D.求证:∠1=∠2.
证明:
在Rt△ABC和Rt△ADC中,
∵AB=AD,
AC=AC,
∴Rt△ABC≌Rt△ADC(HL)
∴∠1=∠2.
巩固练习
[选自教材P21
习题1.3
A组
第1题]
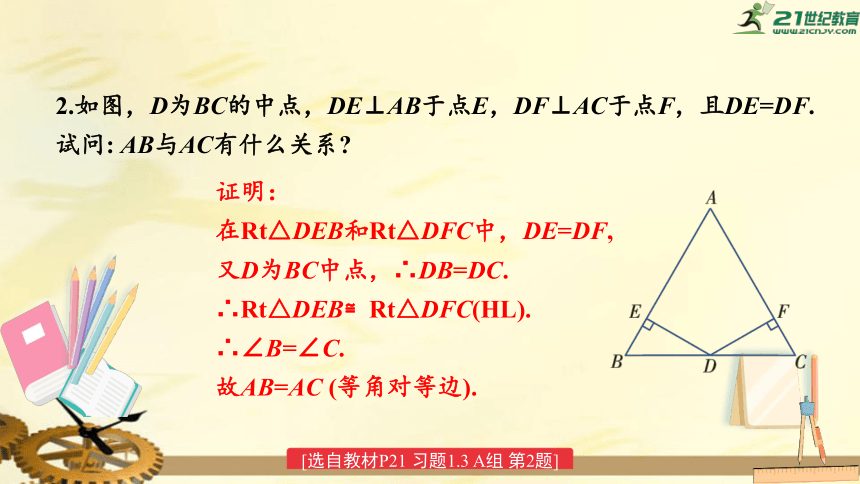
2.如图,D为BC的中点,DE⊥AB于点E,DF⊥AC于点F,且DE=DF.试问:
AB与AC有什么关系?
证明:
在Rt△DEB和Rt△DFC中,DE=DF,
又D为BC中点,∴DB=DC.
∴Rt△DEB≌Rt△DFC(HL).
∴∠B=∠C.
故AB=AC
(等角对等边).
[选自教材P21
习题1.3
A组
第2题]
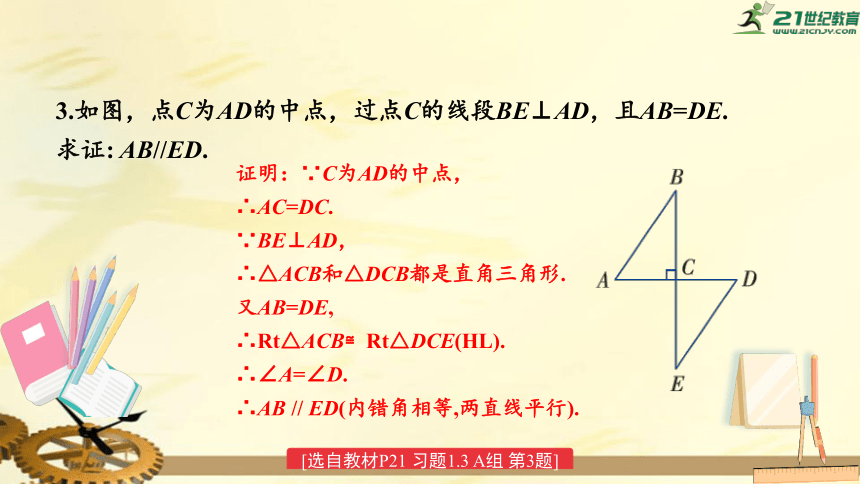
3.如图,点C为AD的中点,过点C的线段BE⊥AD,且AB=DE.
求证:
AB//ED.
证明:∵C为AD的中点,
∴AC=DC.
∵BE⊥AD,
∴△ACB和△DCB都是直角三角形.
又AB=DE,
∴Rt△ACB≌Rt△DCE(HL).
∴∠A=∠D.
∴AB
//
ED(内错角相等,两直线平行).
[选自教材P21
习题1.3
A组
第3题]
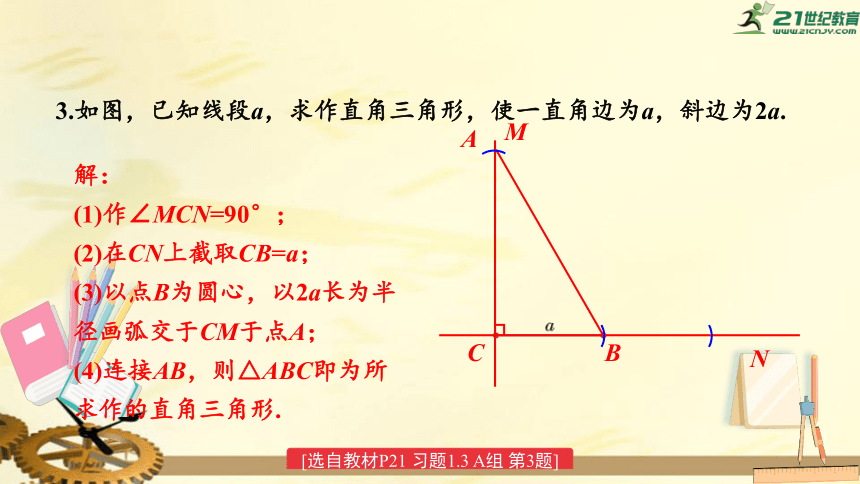
3.如图,已知线段a,求作直角三角形,使一直角边为a,斜边为2a.
解:
(1)作∠MCN=90°;
(2)在CN上截取CB=a;
(3)以点B为圆心,以2a长为半径画弧交于CM于点A;
(4)连接AB,则△ABC即为所求作的直角三角形.
[选自教材P21
习题1.3
A组
第3题]
A
B
C
N
M
5.求证:有两条高相等的三角形是等腰三角形.
已知:在△ABC中,BD⊥AC于D,CE⊥AB于E,且BD=CE.
求证:△ABC是等腰三角形.
证明:
∵BD⊥AC于D,CE⊥AB于E,
∴△CEB和△BDC都是直角三角形.
∵BD=CE,BC=CB
,
∴Rt△CEB≌Rt△BDC
(HL)
∴
∠EBC=∠DCB,
即∠ABC=∠ACB,
∴
AB=AC
(等角对等边).
∴△ABC是等腰三角形.
[选自教材P21
习题1.3
B组
第5题]
6.如图,BD⊥AD于点D,AC⊥BC于点C,且AC=BD.求证:
AD=
BC.
证明:连接AB.
∵BD⊥AD,AC⊥BC,∴∠D=∠C=90°.
又AC=BD,AB=BA,
∴Rt△ADB≌Rt△BCA(HL).
∴AD=BC.
[选自教材P21
习题1.3
B组
第6题]
说一说本节课的收获.
你还存在哪些疑惑?
1
2
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
练习课
第1章
直角三角形
湘教版·八年级数学下册
上课课件
1.如图,AB=AD,CB⊥AB于点B,CD⊥AD于点D.求证:∠1=∠2.
证明:
在Rt△ABC和Rt△ADC中,
∵AB=AD,
AC=AC,
∴Rt△ABC≌Rt△ADC(HL)
∴∠1=∠2.
巩固练习
[选自教材P21
习题1.3
A组
第1题]
2.如图,D为BC的中点,DE⊥AB于点E,DF⊥AC于点F,且DE=DF.试问:
AB与AC有什么关系?
证明:
在Rt△DEB和Rt△DFC中,DE=DF,
又D为BC中点,∴DB=DC.
∴Rt△DEB≌Rt△DFC(HL).
∴∠B=∠C.
故AB=AC
(等角对等边).
[选自教材P21
习题1.3
A组
第2题]
3.如图,点C为AD的中点,过点C的线段BE⊥AD,且AB=DE.
求证:
AB//ED.
证明:∵C为AD的中点,
∴AC=DC.
∵BE⊥AD,
∴△ACB和△DCB都是直角三角形.
又AB=DE,
∴Rt△ACB≌Rt△DCE(HL).
∴∠A=∠D.
∴AB
//
ED(内错角相等,两直线平行).
[选自教材P21
习题1.3
A组
第3题]
3.如图,已知线段a,求作直角三角形,使一直角边为a,斜边为2a.
解:
(1)作∠MCN=90°;
(2)在CN上截取CB=a;
(3)以点B为圆心,以2a长为半径画弧交于CM于点A;
(4)连接AB,则△ABC即为所求作的直角三角形.
[选自教材P21
习题1.3
A组
第3题]
A
B
C
N
M
5.求证:有两条高相等的三角形是等腰三角形.
已知:在△ABC中,BD⊥AC于D,CE⊥AB于E,且BD=CE.
求证:△ABC是等腰三角形.
证明:
∵BD⊥AC于D,CE⊥AB于E,
∴△CEB和△BDC都是直角三角形.
∵BD=CE,BC=CB
,
∴Rt△CEB≌Rt△BDC
(HL)
∴
∠EBC=∠DCB,
即∠ABC=∠ACB,
∴
AB=AC
(等角对等边).
∴△ABC是等腰三角形.
[选自教材P21
习题1.3
B组
第5题]
6.如图,BD⊥AD于点D,AC⊥BC于点C,且AC=BD.求证:
AD=
BC.
证明:连接AB.
∵BD⊥AD,AC⊥BC,∴∠D=∠C=90°.
又AC=BD,AB=BA,
∴Rt△ADB≌Rt△BCA(HL).
∴AD=BC.
[选自教材P21
习题1.3
B组
第6题]
说一说本节课的收获.
你还存在哪些疑惑?
1
2
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
