1.4 角平分线的性质(第1课时 ) 角平分线的性质定理及其逆定理 课件(共22张PPT)
文档属性
| 名称 | 1.4 角平分线的性质(第1课时 ) 角平分线的性质定理及其逆定理 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
角平分线的性质定理及其逆定理
第1章
直角三角形
湘教版·八年级数学下册
上课课件
学习目标
【知识与技能】
让学生通过作图直观地理解角平分线的两个互逆定理.
【过程与方法】
经历探究角的平分线的性质的过程,领会其应用方法.
【情感态度】
激发学生的几何思维,启迪他们的灵感,使学生体会到几何的真正魅力.
【教学重点】
领会角的平分线的两个互逆定理
【教学难点】
两个互逆定理的实际应用
复习导入
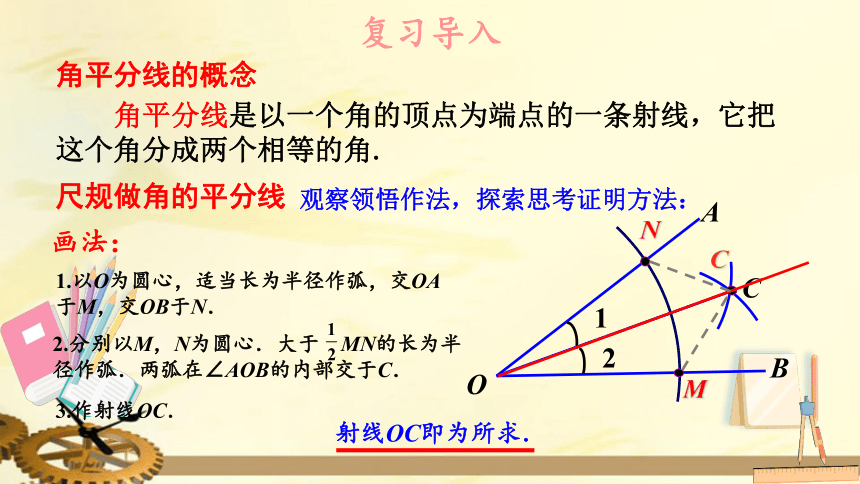
角平分线的概念
O
B
C
A
1
2
角平分线是以一个角的顶点为端点的一条射线,它把这个角分成两个相等的角.
尺规做角的平分线
N
M
C
观察领悟作法,探索思考证明方法:
画法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
2.分别以M,N为圆心.大于
MN的长为半径作弧.两弧在∠AOB的内部交于C.
3.作射线OC.
射线OC即为所求.
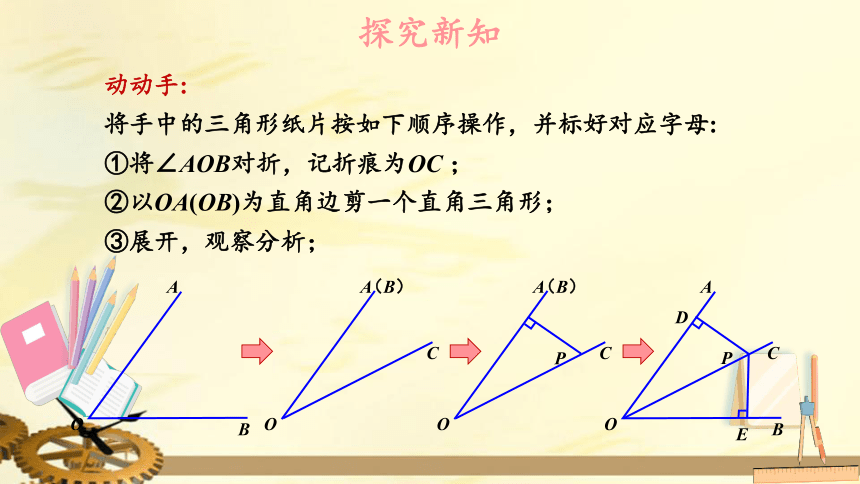
动动手:
将手中的三角形纸片按如下顺序操作,并标好对应字母:
①将∠AOB对折,记折痕为OC
;
②以OA(OB)为直角边剪一个直角三角形;
③展开,观察分析;
探究新知
A
O
B
A
O
C
(B)
A
D
O
P
C
E
B
A
O
C
(B)
P
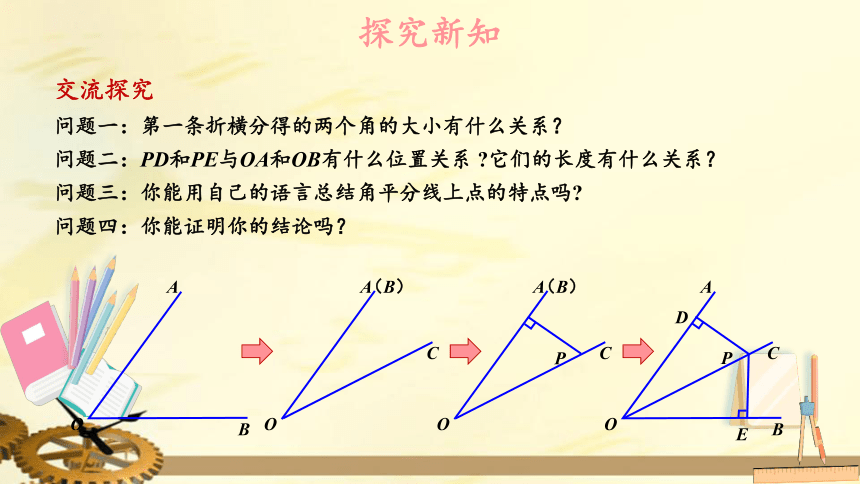
交流探究
问题一:第一条折横分得的两个角的大小有什么关系?
问题二:PD和PE与OA和OB有什么位置关系
?它们的长度有什么关系?
问题三:你能用自己的语言总结角平分线上点的特点吗?
问题四:你能证明你的结论吗?
探究新知
A
O
B
A
O
C
(B)
A
D
O
P
C
E
B
A
O
C
(B)
P
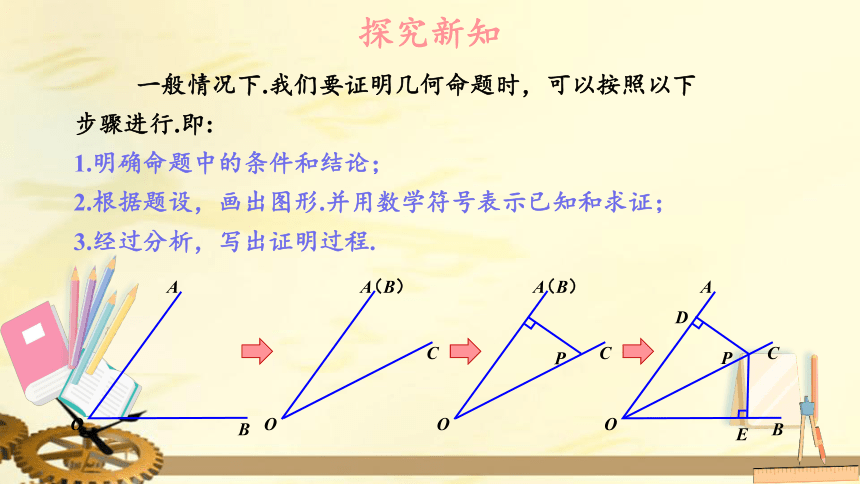
一般情况下.我们要证明几何命题时,可以按照以下步骤进行.即:
1.明确命题中的条件和结论;
2.根据题设,画出图形.并用数学符号表示已知和求证;
3.经过分析,写出证明过程.
探究新知
A
O
B
A
O
C
(B)
A
D
O
P
C
E
B
A
O
C
(B)
P
探究新知
将∠AOB沿OC对折,我发现PD与PE重合,即PD与PE相等.
你能证明吗?
如图1-26,在∠AOB的平分线OC.上任取一点P,作PD⊥OA,PE⊥OB,垂足分别为点D,E,试问PD与PE相等吗?
A
D
O
P
C
E
B
图1-26
由此得到角平分线性质定理:
角的平分线上的点到角的两边的距离相等.
探究新知
如图1-26,在∠AOB的平分线OC.上任取一点P,作PD⊥OA,PE⊥OB,垂足分别为点D,E,试问PD与PE相等吗?
证明:∵PD⊥OA,PE⊥OB.
∴∠PDO=∠PEO=
90°.
在△PDO和△PEO中,∵∠PDO=∠PEO,∠DOP=∠EOP,OP=OP,
∴△PDO≌△PEO.
∴PD=
PE.
A
D
O
P
C
E
B
图1-26
探究新知
如图1-26,在∠AOB的平分线OC.上任取一点P,作PD⊥OA,PE⊥OB,垂足分别为点D,E,试问PD与PE相等吗?
A
D
O
P
C
E
B
图1-26
由此得到角平分线性质定理:
角的平分线上的点到角的两边的距离相等.
符号语言:
∵
OC平分∠AOB,
且PD⊥OA,
PE⊥OB.
∴
PD=PE.
探究新知
角的内部到角的两边距离相等的点在这个角的平分线上吗?
如图1-27,
点P在∠AOB的内部,作PD⊥OA,PE⊥OB.垂足分别为点D,E.若PD=PE,那么点P在∠AOB的平分线上吗?
证明:如图1-27,过点O,
P作射线OC.
∵PD⊥OA,PE⊥OB,∴∠PDO=
∠PEO=
90°.
在Rt△PDO和Rt△PEO中,OP=
OP,PD=PE,
∴Rt△PDO≌Rt△PEO.∴∠AOC=∠BOC.
∴OC是∠AOB的平分线,即点P在∠AOB的平分线OC上.
A
D
O
P
C
E
B
由此得到角平分线性质定理的逆定理:
角的内部到角的两边距离相等的点在角的平分线上.
图1-27
探究新知
角的内部到角的两边距离相等的点在这个角的平分线上吗?
如图1-27,
点P在∠AOB的内部,作PD⊥OA,PE⊥OB.垂足分别为点D,E.若PD=PE,那么点P在∠AOB的平分线上吗?
A
D
O
P
C
E
B
图1-27
由此得到角平分线性质定理的逆定理:
角的内部到角的两边距离相等的点在角的平分线上.
符号语言:
∵
PD⊥OA,PE⊥OB,
PD=PE.
∴
OP平分∠AOB.
图形
名称
图形语言
文字语言
符号语言
关键词
角平分线
性质定理
逆定理
P
C
∵OP平分∠AOB
PD⊥OA于D
PE⊥OB于E
∴PD=PE
角的平分线上的点到角的两边的距离相等.
一平分,
两个垂直,
得一个相等.
P
C
∴OP平分∠AOB
∵PD=PE
PD⊥OA于D
PE⊥OB于E
角的内部到角的两边距离相等的点在角的平分线上.
两个垂直,
一个平分,
得一个相等.
归纳小结
例
1
如图1-28,
∠BAD=∠BCD=90°,∠1=∠2.
(1)求证:
点B在∠ADC的平分线上;
(2)求证:
BD平分∠ABC.
探究新知
证明:(1)在△ABC中,
∵∠l=∠2,∴BA
=
BC.
又BA⊥AD,
BC⊥CD,
∴点B在∠ADC的平分线上.
(2)在Rt△BAD和Rt△中,
∵BA=BC,BD=BD,
∴Rt△BAD≌Rt△BCD.
∴∠ABD=∠CBD.
∴BD平分∠ABC.
巩固练习
1.
如图,在直线MN上求作一点P,使点P到∠AOB两边的距离相等.
E
F
C
P
解:
巩固练习
2.如图,在△ABC中,AD平分∠BAC,
DE⊥AB于点E,DF⊥AC于点F,
BD=CD.
求证:
AB=AC.
证明:∵AD为∠BAC的平分线,
DE⊥AB于E,DF⊥AC于F,
∴DE=DF.
又BD=CD,
∴
Rt△BED≌Rt△CFD.
∴∠B=∠C.
∴AB=AC
(等角对等边).
巩固练习
1.
如图,一个工厂在A区,它到公路、铁路的距离相等,并且离公路和铁路的交叉处O点为500m,在图上标出它的位置(比例尺为1∶20000).
解:
500÷20000=0.025m,
0.025m=2.5cm
图上距离为2.5cm.
E
F
C
P
点P即为所求.
巩固练习
2.如图,在△ABC中,∠C=90°,AC=8
m,DC=
AD,BD平分∠ABC,求D到AB的距离.
解:
课堂小结
角平分线性质定理:
角的平分线上的点到角的两边的距离相等.
角平分线性质定理的逆定理:
角的内部到角的两边距离相等的点在角的平分线上.
课堂小结
角平分线
角平分线上的点到角的两边的距离相等.
角的内部到角的两边距离相等的点在角的平分线上.
定理
逆定理
直
角
三
角
形
性质
判定
直角三角形两个锐角互余.
有两个角互余的三角形是直角三角形.
直角三角形斜边上的中线等于斜边的一半.
三角形一边上的中线等于这条边的一半的三角形是直角三角形.
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.
勾股定理.
勾股定理逆定理.
定理
逆定理
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
角平分线的性质定理及其逆定理
第1章
直角三角形
湘教版·八年级数学下册
上课课件
学习目标
【知识与技能】
让学生通过作图直观地理解角平分线的两个互逆定理.
【过程与方法】
经历探究角的平分线的性质的过程,领会其应用方法.
【情感态度】
激发学生的几何思维,启迪他们的灵感,使学生体会到几何的真正魅力.
【教学重点】
领会角的平分线的两个互逆定理
【教学难点】
两个互逆定理的实际应用
复习导入
角平分线的概念
O
B
C
A
1
2
角平分线是以一个角的顶点为端点的一条射线,它把这个角分成两个相等的角.
尺规做角的平分线
N
M
C
观察领悟作法,探索思考证明方法:
画法:
1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
2.分别以M,N为圆心.大于
MN的长为半径作弧.两弧在∠AOB的内部交于C.
3.作射线OC.
射线OC即为所求.
动动手:
将手中的三角形纸片按如下顺序操作,并标好对应字母:
①将∠AOB对折,记折痕为OC
;
②以OA(OB)为直角边剪一个直角三角形;
③展开,观察分析;
探究新知
A
O
B
A
O
C
(B)
A
D
O
P
C
E
B
A
O
C
(B)
P
交流探究
问题一:第一条折横分得的两个角的大小有什么关系?
问题二:PD和PE与OA和OB有什么位置关系
?它们的长度有什么关系?
问题三:你能用自己的语言总结角平分线上点的特点吗?
问题四:你能证明你的结论吗?
探究新知
A
O
B
A
O
C
(B)
A
D
O
P
C
E
B
A
O
C
(B)
P
一般情况下.我们要证明几何命题时,可以按照以下步骤进行.即:
1.明确命题中的条件和结论;
2.根据题设,画出图形.并用数学符号表示已知和求证;
3.经过分析,写出证明过程.
探究新知
A
O
B
A
O
C
(B)
A
D
O
P
C
E
B
A
O
C
(B)
P
探究新知
将∠AOB沿OC对折,我发现PD与PE重合,即PD与PE相等.
你能证明吗?
如图1-26,在∠AOB的平分线OC.上任取一点P,作PD⊥OA,PE⊥OB,垂足分别为点D,E,试问PD与PE相等吗?
A
D
O
P
C
E
B
图1-26
由此得到角平分线性质定理:
角的平分线上的点到角的两边的距离相等.
探究新知
如图1-26,在∠AOB的平分线OC.上任取一点P,作PD⊥OA,PE⊥OB,垂足分别为点D,E,试问PD与PE相等吗?
证明:∵PD⊥OA,PE⊥OB.
∴∠PDO=∠PEO=
90°.
在△PDO和△PEO中,∵∠PDO=∠PEO,∠DOP=∠EOP,OP=OP,
∴△PDO≌△PEO.
∴PD=
PE.
A
D
O
P
C
E
B
图1-26
探究新知
如图1-26,在∠AOB的平分线OC.上任取一点P,作PD⊥OA,PE⊥OB,垂足分别为点D,E,试问PD与PE相等吗?
A
D
O
P
C
E
B
图1-26
由此得到角平分线性质定理:
角的平分线上的点到角的两边的距离相等.
符号语言:
∵
OC平分∠AOB,
且PD⊥OA,
PE⊥OB.
∴
PD=PE.
探究新知
角的内部到角的两边距离相等的点在这个角的平分线上吗?
如图1-27,
点P在∠AOB的内部,作PD⊥OA,PE⊥OB.垂足分别为点D,E.若PD=PE,那么点P在∠AOB的平分线上吗?
证明:如图1-27,过点O,
P作射线OC.
∵PD⊥OA,PE⊥OB,∴∠PDO=
∠PEO=
90°.
在Rt△PDO和Rt△PEO中,OP=
OP,PD=PE,
∴Rt△PDO≌Rt△PEO.∴∠AOC=∠BOC.
∴OC是∠AOB的平分线,即点P在∠AOB的平分线OC上.
A
D
O
P
C
E
B
由此得到角平分线性质定理的逆定理:
角的内部到角的两边距离相等的点在角的平分线上.
图1-27
探究新知
角的内部到角的两边距离相等的点在这个角的平分线上吗?
如图1-27,
点P在∠AOB的内部,作PD⊥OA,PE⊥OB.垂足分别为点D,E.若PD=PE,那么点P在∠AOB的平分线上吗?
A
D
O
P
C
E
B
图1-27
由此得到角平分线性质定理的逆定理:
角的内部到角的两边距离相等的点在角的平分线上.
符号语言:
∵
PD⊥OA,PE⊥OB,
PD=PE.
∴
OP平分∠AOB.
图形
名称
图形语言
文字语言
符号语言
关键词
角平分线
性质定理
逆定理
P
C
∵OP平分∠AOB
PD⊥OA于D
PE⊥OB于E
∴PD=PE
角的平分线上的点到角的两边的距离相等.
一平分,
两个垂直,
得一个相等.
P
C
∴OP平分∠AOB
∵PD=PE
PD⊥OA于D
PE⊥OB于E
角的内部到角的两边距离相等的点在角的平分线上.
两个垂直,
一个平分,
得一个相等.
归纳小结
例
1
如图1-28,
∠BAD=∠BCD=90°,∠1=∠2.
(1)求证:
点B在∠ADC的平分线上;
(2)求证:
BD平分∠ABC.
探究新知
证明:(1)在△ABC中,
∵∠l=∠2,∴BA
=
BC.
又BA⊥AD,
BC⊥CD,
∴点B在∠ADC的平分线上.
(2)在Rt△BAD和Rt△中,
∵BA=BC,BD=BD,
∴Rt△BAD≌Rt△BCD.
∴∠ABD=∠CBD.
∴BD平分∠ABC.
巩固练习
1.
如图,在直线MN上求作一点P,使点P到∠AOB两边的距离相等.
E
F
C
P
解:
巩固练习
2.如图,在△ABC中,AD平分∠BAC,
DE⊥AB于点E,DF⊥AC于点F,
BD=CD.
求证:
AB=AC.
证明:∵AD为∠BAC的平分线,
DE⊥AB于E,DF⊥AC于F,
∴DE=DF.
又BD=CD,
∴
Rt△BED≌Rt△CFD.
∴∠B=∠C.
∴AB=AC
(等角对等边).
巩固练习
1.
如图,一个工厂在A区,它到公路、铁路的距离相等,并且离公路和铁路的交叉处O点为500m,在图上标出它的位置(比例尺为1∶20000).
解:
500÷20000=0.025m,
0.025m=2.5cm
图上距离为2.5cm.
E
F
C
P
点P即为所求.
巩固练习
2.如图,在△ABC中,∠C=90°,AC=8
m,DC=
AD,BD平分∠ABC,求D到AB的距离.
解:
课堂小结
角平分线性质定理:
角的平分线上的点到角的两边的距离相等.
角平分线性质定理的逆定理:
角的内部到角的两边距离相等的点在角的平分线上.
课堂小结
角平分线
角平分线上的点到角的两边的距离相等.
角的内部到角的两边距离相等的点在角的平分线上.
定理
逆定理
直
角
三
角
形
性质
判定
直角三角形两个锐角互余.
有两个角互余的三角形是直角三角形.
直角三角形斜边上的中线等于斜边的一半.
三角形一边上的中线等于这条边的一半的三角形是直角三角形.
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.
勾股定理.
勾股定理逆定理.
定理
逆定理
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
