1.4 角平分线的性质(第2课时) 角平分线的性质定理及其逆定理的综合应用 课件(共10张PPT)
文档属性
| 名称 | 1.4 角平分线的性质(第2课时) 角平分线的性质定理及其逆定理的综合应用 课件(共10张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
角平分线性质定理及其逆定理的综合应用
第1章
直角三角形
湘教版·八年级数学下册
上课课件
学习目标
【知识与技能】
让学生在掌握角平分线的性质的基础上能应用角平分线的两个性质解决一些简单的实际问题.
【过程与方法】
通过让学生经历动手实践,合作交流,演绎推理的过程,使学生学会理性思维,从而提高解决简单问题的能力.
【情感态度】
经历对角的平分线的性质的探索与形成的过程,发展应用数学知识的意识与能力,培养学生的联想、探索、概括归纳的能力,激发学生学习数学的兴趣.
【教学重点】
角平分线的性质及其应用
【教学难点】
灵活应用两个性质解决问题
情境导入
P
S区
公路
铁路
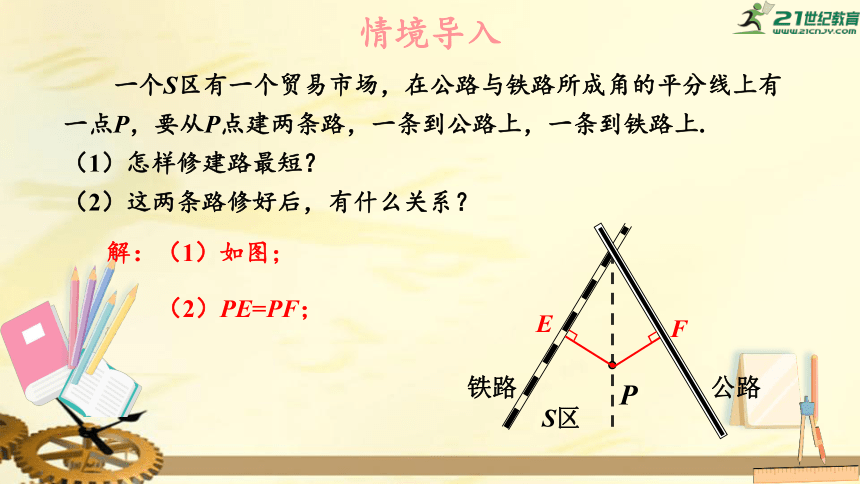
一个S区有一个贸易市场,在公路与铁路所成角的平分线上有一点P,要从P点建两条路,一条到公路上,一条到铁路上.
(1)怎样修建路最短?
(2)这两条路修好后,有什么关系?
E
F
解:(1)如图;
(2)PE=PF;
新课引入
如图1-29,已知EF⊥CD,EF⊥AB,MN⊥AC,M是EF的中点.需添加一个什么条件,就可使CM,AM分别为∠ACD和∠CAB的平分线呢?
解:可以添加条件MN=ME
(或MN=
MF).
∵ME⊥CD,MN⊥CA,
∴M在∠ACD的平分线上,即CM是∠ACD的平分线.
同理可得AM是∠CAB的平分线.
如图1-30,
在△ABC的外角∠DAC的平分线上任取一点P,作PE⊥DB,
PF⊥AC,垂足分别为点E,F.试探索BE+PF与PB的大小关系.
新课引入
例
2
解:∵AP是∠DAC的平分线,
又PE⊥DB,PF⊥AC,
∴PE=
PF.
在△EBP中,BE+
PE>
PB
∴BE+
PF>
PB.
【教材P25】
探究新知
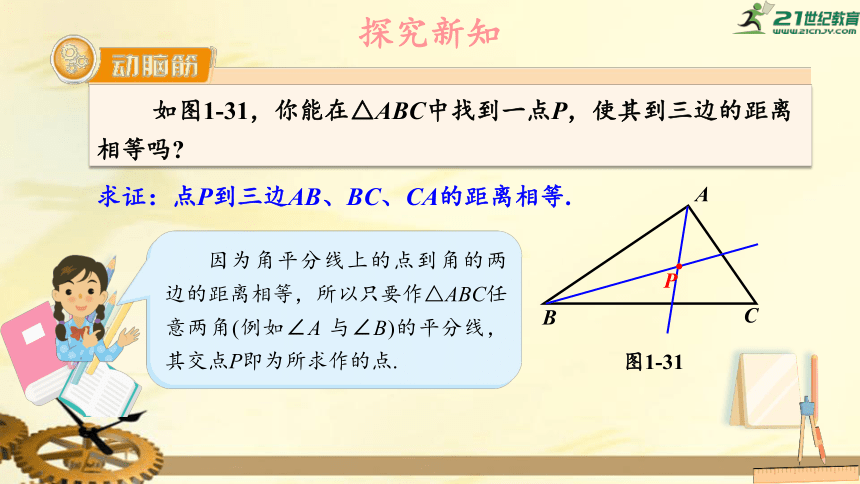
如图1-31,你能在△ABC中找到一点P,使其到三边的距离相等吗?
A
B
C
图1-31
P
因为角平分线上的点到角的两边的距离相等,所以只要作△ABC任意两角(例如∠A
与∠B)的平分线,其交点P即为所求作的点.
求证:点P到三边AB、BC、CA的距离相等.
探究新知
如图1-31,你能在△ABC中找到一点P,使其到三边的距离相等吗?
A
B
C
图1-31
M
P
D
F
E
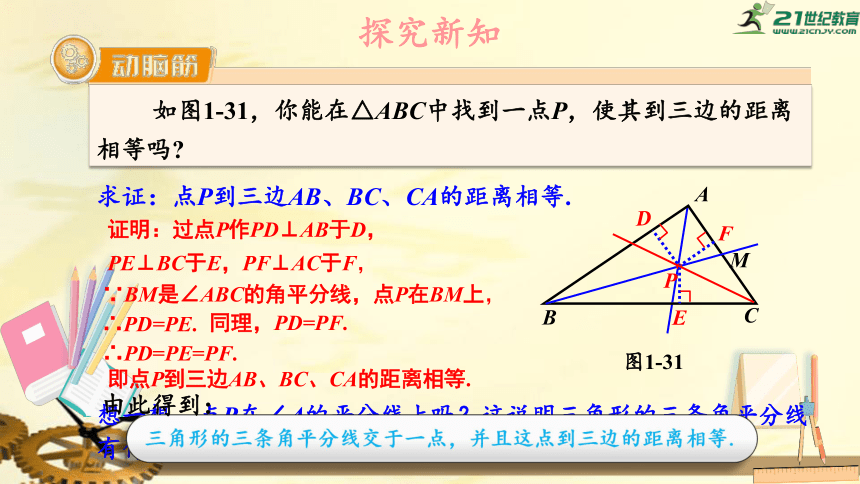
∵BM是∠ABC的角平分线,点P在BM上,
∴PD=PE.
同理,PD=PF.
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等.
证明:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F,
想一想,点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?
求证:点P到三边AB、BC、CA的距离相等.
三角形的三条角平分线交于一点,并且这点到三边的距离相等.
由此得到:
巩固练习
1.
如图,E是∠AOB的平分线上一点,EC⊥OA于点C,ED⊥OB于点D,求证:
(1)∠ECD=∠EDC;
(2)
OC=OD.
证明:(1)∵OE是∠AOB的平分线,
EC⊥OA,ED⊥OB,
∴EC=ED.
∴∠ECD=∠EDC.
(2)在Rt△ECO和Rt△EDO中,
∵EC=ED,OE为公共边,
∴Rt△ECO≌Rt△EDO
(HL).
∴OC=OD.
巩固练习
2.如图,在△ABC中,AD⊥DE,BE⊥DE,AC,BC分别平分∠BAD,∠ABE,点C在线段DE上.求证:
AB=AD+
BE.
证明:过点C作CF⊥AB于点F.
又AC是∠BAD的平分线,CD⊥AD,
∴CF=CD.
在Rt△CFA和Rt△CDA中,
∵CF=CD,
AC为公共边,∴Rt△CFA≌Rt△CDA
(HL).
∴AF=AD.
同理可得FB=BE.
AB=A
F+FB=AD+BE.
F
巩固练习
3.如图,已知BD平分∠ABC,BA=BC,点P在BD上,作PM⊥AD,PN⊥CD,垂足分别为点M,N.求证:
PM=PN.
证明:BD平分∠ABC,
∴∠ABD=∠CBD.
又BA=BC,BD为公共边,
∴△ABD≌△CBD(SAS).
∴∠ADB=∠CDB.
又PM⊥AD,
PN⊥CD,
∴
PM=PN.
巩固练习
4.如图,求作一点P,使PM=PN,并且使点P到∠AOB的两边OA,OB的距离相等.
P
解:作法如图.
巩固练习
5.如图,已知△ABC的外角∠CBD和∠BCE的平分线BF,CF相交于点F,试问点F在∠A
的平分线上吗?
(提示:过F点分别向BD,
BC,
CE作垂线)
解:过点F作FH⊥AD于H,FG⊥BC于G,FR⊥AE于R,则可得FH=FG=FR.
∴点F在∠A的平分线上.
说一说本节课的收获.
你还存在哪些疑惑?
课堂小结
1
2
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
角平分线性质定理及其逆定理的综合应用
第1章
直角三角形
湘教版·八年级数学下册
上课课件
学习目标
【知识与技能】
让学生在掌握角平分线的性质的基础上能应用角平分线的两个性质解决一些简单的实际问题.
【过程与方法】
通过让学生经历动手实践,合作交流,演绎推理的过程,使学生学会理性思维,从而提高解决简单问题的能力.
【情感态度】
经历对角的平分线的性质的探索与形成的过程,发展应用数学知识的意识与能力,培养学生的联想、探索、概括归纳的能力,激发学生学习数学的兴趣.
【教学重点】
角平分线的性质及其应用
【教学难点】
灵活应用两个性质解决问题
情境导入
P
S区
公路
铁路
一个S区有一个贸易市场,在公路与铁路所成角的平分线上有一点P,要从P点建两条路,一条到公路上,一条到铁路上.
(1)怎样修建路最短?
(2)这两条路修好后,有什么关系?
E
F
解:(1)如图;
(2)PE=PF;
新课引入
如图1-29,已知EF⊥CD,EF⊥AB,MN⊥AC,M是EF的中点.需添加一个什么条件,就可使CM,AM分别为∠ACD和∠CAB的平分线呢?
解:可以添加条件MN=ME
(或MN=
MF).
∵ME⊥CD,MN⊥CA,
∴M在∠ACD的平分线上,即CM是∠ACD的平分线.
同理可得AM是∠CAB的平分线.
如图1-30,
在△ABC的外角∠DAC的平分线上任取一点P,作PE⊥DB,
PF⊥AC,垂足分别为点E,F.试探索BE+PF与PB的大小关系.
新课引入
例
2
解:∵AP是∠DAC的平分线,
又PE⊥DB,PF⊥AC,
∴PE=
PF.
在△EBP中,BE+
PE>
PB
∴BE+
PF>
PB.
【教材P25】
探究新知
如图1-31,你能在△ABC中找到一点P,使其到三边的距离相等吗?
A
B
C
图1-31
P
因为角平分线上的点到角的两边的距离相等,所以只要作△ABC任意两角(例如∠A
与∠B)的平分线,其交点P即为所求作的点.
求证:点P到三边AB、BC、CA的距离相等.
探究新知
如图1-31,你能在△ABC中找到一点P,使其到三边的距离相等吗?
A
B
C
图1-31
M
P
D
F
E
∵BM是∠ABC的角平分线,点P在BM上,
∴PD=PE.
同理,PD=PF.
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等.
证明:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F,
想一想,点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?
求证:点P到三边AB、BC、CA的距离相等.
三角形的三条角平分线交于一点,并且这点到三边的距离相等.
由此得到:
巩固练习
1.
如图,E是∠AOB的平分线上一点,EC⊥OA于点C,ED⊥OB于点D,求证:
(1)∠ECD=∠EDC;
(2)
OC=OD.
证明:(1)∵OE是∠AOB的平分线,
EC⊥OA,ED⊥OB,
∴EC=ED.
∴∠ECD=∠EDC.
(2)在Rt△ECO和Rt△EDO中,
∵EC=ED,OE为公共边,
∴Rt△ECO≌Rt△EDO
(HL).
∴OC=OD.
巩固练习
2.如图,在△ABC中,AD⊥DE,BE⊥DE,AC,BC分别平分∠BAD,∠ABE,点C在线段DE上.求证:
AB=AD+
BE.
证明:过点C作CF⊥AB于点F.
又AC是∠BAD的平分线,CD⊥AD,
∴CF=CD.
在Rt△CFA和Rt△CDA中,
∵CF=CD,
AC为公共边,∴Rt△CFA≌Rt△CDA
(HL).
∴AF=AD.
同理可得FB=BE.
AB=A
F+FB=AD+BE.
F
巩固练习
3.如图,已知BD平分∠ABC,BA=BC,点P在BD上,作PM⊥AD,PN⊥CD,垂足分别为点M,N.求证:
PM=PN.
证明:BD平分∠ABC,
∴∠ABD=∠CBD.
又BA=BC,BD为公共边,
∴△ABD≌△CBD(SAS).
∴∠ADB=∠CDB.
又PM⊥AD,
PN⊥CD,
∴
PM=PN.
巩固练习
4.如图,求作一点P,使PM=PN,并且使点P到∠AOB的两边OA,OB的距离相等.
P
解:作法如图.
巩固练习
5.如图,已知△ABC的外角∠CBD和∠BCE的平分线BF,CF相交于点F,试问点F在∠A
的平分线上吗?
(提示:过F点分别向BD,
BC,
CE作垂线)
解:过点F作FH⊥AD于H,FG⊥BC于G,FR⊥AE于R,则可得FH=FG=FR.
∴点F在∠A的平分线上.
说一说本节课的收获.
你还存在哪些疑惑?
课堂小结
1
2
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
