第1章 直角三角形 小结与复习(复习题1) 课件(共20张PPT)
文档属性
| 名称 | 第1章 直角三角形 小结与复习(复习题1) 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 14:44:50 | ||
图片预览







文档简介
(共20张PPT)
小结与复习
第1章
直角三角形
湘教版·八年级数学下册
上课课件
学习目标
【知识与技能】
1.系统了解本章的知识体系及知识内容.
2.在熟练掌握直角三角形相关概念的基础上,进一步熟悉掌握直角三角形性质与判定的应用.
3.在掌握角平分线性质及其逆定理的基础上将知识融汇贯通,进行一些提高训练.
4.培养对知识综合掌握、综合运用的能力.
【过程与方法】
复习梳理本章的主要知识点,及应注意的问题.通过典型例题讲解和对应练习,使学生对本章知识达标.
【情感态度】
主动参与、积极探索、合作交流,发挥学习中主人翁意识,感受成功的乐趣,激发学生的学习兴趣,培养学生的动手操作能力和解决问题的能力.
【教学重点】
勾股定理及其逆定理,直角三角形的性质和判定,角平分线性质与判定在解决实际问题中的作用.
【教学难点】
综合运用直角三角形相关知识解决问题.
1.直角三角形的两个锐角有什么关系?
2.直角三角形斜边上的中线与斜边有什么关系?
3.请用自己的语言叙述勾股定理及其逆定理.
4.判断两个直角三角形全等的方法有哪些?
5.角平分线有哪些性质?
小结复习
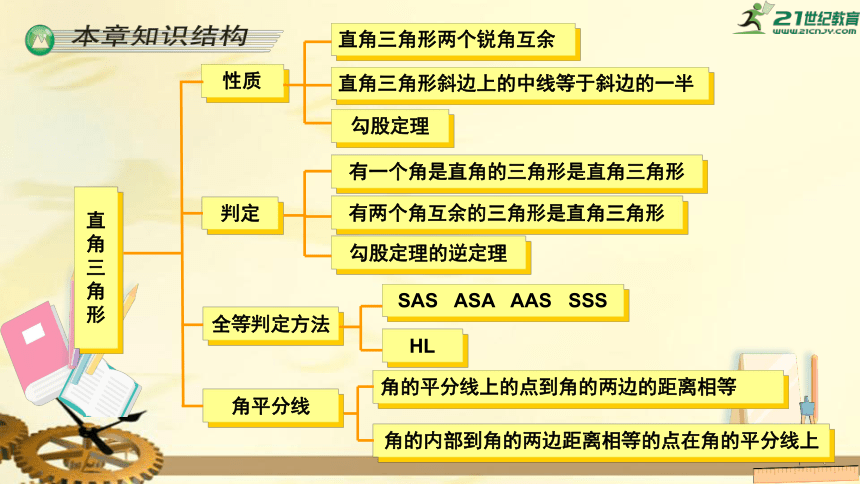
性质
直
角
三
角
形
直角三角形两个锐角互余
直角三角形斜边上的中线等于斜边的一半
勾股定理
SAS
ASA
AAS
SSS
HL
判定
全等判定方法
角的平分线上的点到角的两边的距离相等
角的内部到角的两边距离相等的点在角的平分线上
有一个角是直角的三角形是直角三角形
有两个角互余的三角形是直角三角形
勾股定理的逆定理
角平分线
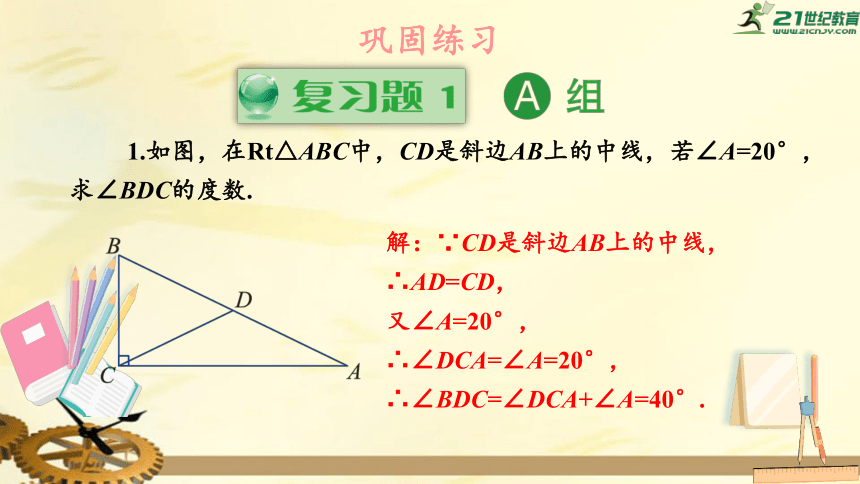
1.如图,在Rt△ABC中,CD是斜边AB上的中线,若∠A=20°,求∠BDC的度数.
解:∵CD是斜边AB上的中线,
∴AD=CD,
又∠A=20°,
∴∠DCA=∠A=20°,
∴∠BDC=∠DCA+∠A=40°.
巩固练习
2.如图,在Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AC于点E,∠A=30°,AB=8,求DE的长.
解:
∵D为AB的中点,
AB=8,
∴AD=BD=4,
又在Rt△ABC中,
∠A=30°,
∴DE=2.
3.用计算器求图中的x
(结果精确到0.1
m).
4.判断由a,b,
c组成的三角形是不是直角三角形.
(1)a=15,b=8,c=17;
(2)
a=
,b=1,c=
;
(3)a=1.5,b=2,c=2.5.
解:
5.已知A,B两艘船同时从港口O出发,船A以15
km/h的速度向东航行;船B以10km/h的速度向北航行.它们离开港口2h后,相距多远?
解:AO=15×2=30(km)
BO=10×2=20(km)
答:它们离开港口2h后,相距
km.
6.如图,点B,
E,
C,
F在同一直线上,∠A=∠D=90°,BE=FC,
AB=DF.求证:∠ACB=∠DEF.
证明:∵∠A=∠D=90°
∴△ABC和△DFE是直角三角形..
∵BE=FC,
∴BE+EC=FC+EC.
即BC=FE.
又AB=DF,
∴Rt△ABC≌Rt△DFE(HL).
∴∠ACB=∠DEF
(全等三角形对应角相等).
7.如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP//
OB,交OA于点C,PD⊥OB,垂足为点D,且PC=4,求PD的长.
解:过点P作PE⊥OA于点E,
∵CP//OB,
∠AOB=30°,
∴∠ACP=∠AOB=30°.
在Rt△PEC中,
∵∠ACP=30°,
∴PE=
PC=
×4=2:
∵点P在∠AOB的平分线上,又PD⊥OB于点D,
∴PD=PE=2.
8.如图,在一棵树的5m高处有两只猴子,其中一只猴子爬下来走向离树15m处的池塘,而另一只爬到树顶后直扑池塘(假设其下落的轨迹为直线).如果两只猴子经过的路程相等,那么这棵树有多高呢?
解:设另一只猴子在树上爬了xm,由题意,得
(5+x)2+152=
(15+5-x)2,
x=3
答:这棵树有8m高.
9.已知直角三角形两直角边的和为
,斜边长为2,求这个直角三角形的面积.
10.如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线且交BC于点D,DE⊥AB,垂足为点E,若AB=12
cm,求△DEB的周长.
解:AD是∠BAC的平分线,DE⊥AB于E,DC⊥AC于C,
∴DE=CD.
易证AE=AC=BC.
∴BD+DE+EB=BD+CD+EB=BC+EB
=AE+EB=AB=12
cm.
∴△DEB的周长为12
cm.
11.如图,小明和小强攀登一无名山峰,他俩在山脚A处测得主峰B的仰角为45°,然后从山脚沿一段倾角为30°的斜坡走了2km到达山腰C,此时测得主峰B的仰角为60°.于是小明对小强说:“我知道主峰多高了.”你能根据他们的数据算出主峰的高度吗?
解:∵∠ABC=∠BAC=15°,∴BC=AC=2
km,
在Rt△BCD中,CD=1
km
,BD=
km,
主峰高度为(1+
)
km.
12.图(a)
表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A,当钟面显示3点30分时,分针垂直于桌面,A点距桌面的高度为10cm.如图(b),若此钟面显示3点45分时,A点距桌面的高度为16cm.则当钟面显示3点50分时,A点距桌面的高度为多少?
解:如图,由已知条件可知
OA1=OA2=OA3=6cm
作A3H⊥OA2于H,
则∠A3OH=30°,OA3=6,
∴A3H=
OA3=
×6=3.
∴此时点A到桌面的距离为19cm.
说一说本节课的收获.
你还存在哪些疑惑?
1
2
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
小结与复习
第1章
直角三角形
湘教版·八年级数学下册
上课课件
学习目标
【知识与技能】
1.系统了解本章的知识体系及知识内容.
2.在熟练掌握直角三角形相关概念的基础上,进一步熟悉掌握直角三角形性质与判定的应用.
3.在掌握角平分线性质及其逆定理的基础上将知识融汇贯通,进行一些提高训练.
4.培养对知识综合掌握、综合运用的能力.
【过程与方法】
复习梳理本章的主要知识点,及应注意的问题.通过典型例题讲解和对应练习,使学生对本章知识达标.
【情感态度】
主动参与、积极探索、合作交流,发挥学习中主人翁意识,感受成功的乐趣,激发学生的学习兴趣,培养学生的动手操作能力和解决问题的能力.
【教学重点】
勾股定理及其逆定理,直角三角形的性质和判定,角平分线性质与判定在解决实际问题中的作用.
【教学难点】
综合运用直角三角形相关知识解决问题.
1.直角三角形的两个锐角有什么关系?
2.直角三角形斜边上的中线与斜边有什么关系?
3.请用自己的语言叙述勾股定理及其逆定理.
4.判断两个直角三角形全等的方法有哪些?
5.角平分线有哪些性质?
小结复习
性质
直
角
三
角
形
直角三角形两个锐角互余
直角三角形斜边上的中线等于斜边的一半
勾股定理
SAS
ASA
AAS
SSS
HL
判定
全等判定方法
角的平分线上的点到角的两边的距离相等
角的内部到角的两边距离相等的点在角的平分线上
有一个角是直角的三角形是直角三角形
有两个角互余的三角形是直角三角形
勾股定理的逆定理
角平分线
1.如图,在Rt△ABC中,CD是斜边AB上的中线,若∠A=20°,求∠BDC的度数.
解:∵CD是斜边AB上的中线,
∴AD=CD,
又∠A=20°,
∴∠DCA=∠A=20°,
∴∠BDC=∠DCA+∠A=40°.
巩固练习
2.如图,在Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AC于点E,∠A=30°,AB=8,求DE的长.
解:
∵D为AB的中点,
AB=8,
∴AD=BD=4,
又在Rt△ABC中,
∠A=30°,
∴DE=2.
3.用计算器求图中的x
(结果精确到0.1
m).
4.判断由a,b,
c组成的三角形是不是直角三角形.
(1)a=15,b=8,c=17;
(2)
a=
,b=1,c=
;
(3)a=1.5,b=2,c=2.5.
解:
5.已知A,B两艘船同时从港口O出发,船A以15
km/h的速度向东航行;船B以10km/h的速度向北航行.它们离开港口2h后,相距多远?
解:AO=15×2=30(km)
BO=10×2=20(km)
答:它们离开港口2h后,相距
km.
6.如图,点B,
E,
C,
F在同一直线上,∠A=∠D=90°,BE=FC,
AB=DF.求证:∠ACB=∠DEF.
证明:∵∠A=∠D=90°
∴△ABC和△DFE是直角三角形..
∵BE=FC,
∴BE+EC=FC+EC.
即BC=FE.
又AB=DF,
∴Rt△ABC≌Rt△DFE(HL).
∴∠ACB=∠DEF
(全等三角形对应角相等).
7.如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP//
OB,交OA于点C,PD⊥OB,垂足为点D,且PC=4,求PD的长.
解:过点P作PE⊥OA于点E,
∵CP//OB,
∠AOB=30°,
∴∠ACP=∠AOB=30°.
在Rt△PEC中,
∵∠ACP=30°,
∴PE=
PC=
×4=2:
∵点P在∠AOB的平分线上,又PD⊥OB于点D,
∴PD=PE=2.
8.如图,在一棵树的5m高处有两只猴子,其中一只猴子爬下来走向离树15m处的池塘,而另一只爬到树顶后直扑池塘(假设其下落的轨迹为直线).如果两只猴子经过的路程相等,那么这棵树有多高呢?
解:设另一只猴子在树上爬了xm,由题意,得
(5+x)2+152=
(15+5-x)2,
x=3
答:这棵树有8m高.
9.已知直角三角形两直角边的和为
,斜边长为2,求这个直角三角形的面积.
10.如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线且交BC于点D,DE⊥AB,垂足为点E,若AB=12
cm,求△DEB的周长.
解:AD是∠BAC的平分线,DE⊥AB于E,DC⊥AC于C,
∴DE=CD.
易证AE=AC=BC.
∴BD+DE+EB=BD+CD+EB=BC+EB
=AE+EB=AB=12
cm.
∴△DEB的周长为12
cm.
11.如图,小明和小强攀登一无名山峰,他俩在山脚A处测得主峰B的仰角为45°,然后从山脚沿一段倾角为30°的斜坡走了2km到达山腰C,此时测得主峰B的仰角为60°.于是小明对小强说:“我知道主峰多高了.”你能根据他们的数据算出主峰的高度吗?
解:∵∠ABC=∠BAC=15°,∴BC=AC=2
km,
在Rt△BCD中,CD=1
km
,BD=
km,
主峰高度为(1+
)
km.
12.图(a)
表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A,当钟面显示3点30分时,分针垂直于桌面,A点距桌面的高度为10cm.如图(b),若此钟面显示3点45分时,A点距桌面的高度为16cm.则当钟面显示3点50分时,A点距桌面的高度为多少?
解:如图,由已知条件可知
OA1=OA2=OA3=6cm
作A3H⊥OA2于H,
则∠A3OH=30°,OA3=6,
∴A3H=
OA3=
×6=3.
∴此时点A到桌面的距离为19cm.
说一说本节课的收获.
你还存在哪些疑惑?
1
2
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
