1.4 角平分线 课件(共17张PPT)
文档属性
| 名称 | 1.4 角平分线 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 14:46:06 | ||
图片预览






文档简介
(共17张PPT)
数学教学PPT
北师大版
八年级下
三
角
形
的
证
明
角平分线
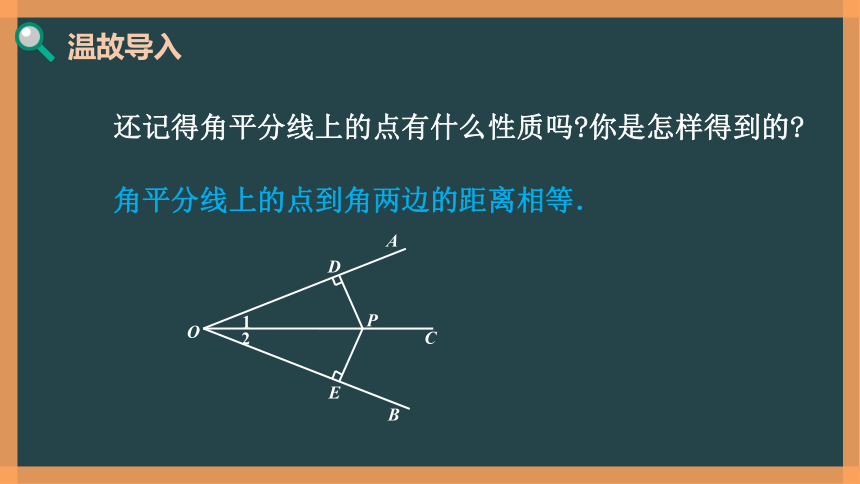
还记得角平分线上的点有什么性质吗?你是怎样得到的?
角平分线上的点到角两边的距离相等.
温故导入
2
1
E
D
C
P
O
B
A
已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D、E.
求证:PD=PE.
证明:∵∠1=∠2,OP=OP,∠PDO=∠PEO=90°,
∴△PDO≌△PEO(AAS).
∴PD=PE(全等三角形的对应边相等)
2
1
E
D
C
P
O
B
A
小试牛刀
如果有一个点到角两边的距离相等,那么这个点必在这个角的平分线上.
你能写出这个定理的逆命题吗?
这个命题是假命题.角平分线是角内部的一条射线,而角的外部也存在到角两边距离相等的点.
角平分线性质定理的逆命题:在一个角的内部且到角的两边距离相等的点,在这个角的角平分线上.
这是一个真命题吗?
小试牛刀
已知:在∠AOB内部有一点P,且PD⊥OA,PE⊥OB,D、E为垂足且PD=PE,求证:点P在∠AOB的角平分线上.
证明:∵PD⊥OA,PE⊥OB,
∴∠PDO=∠
PEO=90°;
在Rt△ODP和Rt△OEP中,OP=OP,PD=PE
∴Rt△ODP
≌
Rt△OEP(HL).
∴∠1=∠2(全等三角形对应角相等).
2
1
E
D
C
P
O
B
A
大放异彩
解:
∵DE
⊥
AB,DF
⊥
AC,垂足分别为E,
F,且DE=DF,
∴AD平分∠BAC(在一个角的内部,到角的
E
两边距
离相等的点在这个角的平分线上).
又∵
∠BAC=60°,
∴
∠BAD=30°.
在Rt
△
ADE中,
∠AED=90°,AD=10,
∴DE=
2
AD=
2
×10=5(在直角三角形中,
如果一个锐角等
于30°,那么它所对的直角
边等于斜边的一半).
大放异彩
例题:在
△ABC
中,∠
BAC
=
60°,点
D
在
BC
上,AD
=
10,DE⊥AB,DF⊥AC,垂足分别为
E,F,且
DE
=
DF,求
DE
的长.
三角形的三个内角的角平分线,你发现了什么?
发现:三角形的三个内角的角平分线交于一点.这一点到三角形三边的距离相等.
仔细思考
剪一个三角形纸片,通过折叠找出每个角的角平分线,观察这三条角平分线,你是否发现同样的结论?与同伴交流.
D
F
E
M
N
C
B
A
P
仔细思考
D
E
F
M
N
C
B
A
P
证明:三角形三条角平分线相交于一点.
已知:如图,设△ABC的角平分线.BM、CN相交于点P,求证:P点在∠BAC的角平分线上.
证明:过P点作PD⊥AB,PF⊥AC,PE⊥BC,
其中D、E、F是垂足
∵BM是△ABC的角平分线,点P在BM上∴PD=PE
同理:PE=PF.∴PD=PF.∴点P在∠BAC的平分线上
∴△ABC的三条角平分线相交于点P.
探索求证
如图:直线L1、L2、L3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可选择的地址有几处?
满足条件共4个
P
1
P
l
3
l
2
1
l
C
B
A
拓展创新
[例1]如图,在△ABC中.AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)已知CD=4
cm,求AC的长;(2)求证:AB=AC+CD.
D
A
B
E
C
(1)解:∵AD是△ABC的角平分线,∠C=90°,DE⊥AB
∴DE=CD=4cm;∵AC=BC
∴∠B=∠BAC(等边对等角)
∵∠C=90°,∴∠B=1/2×90°=45°.
∴∠BDE=90°—45°=45°.∴BE=DE(等角对等边).
在等腰直角三角形BDE中(勾股定理)∴AC=BC=CD+BD=(4+4)cm.
拓展练习
[例1]如图,在△ABC中.AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)已知CD=4
cm,求AC的长;(2)求证:AB=AC+CD.
D
A
B
E
C
(2)证明:由(1)的求解过程可知,
Rt△ACD≌Rt△AED(HL)
∴AC=AE.
∵BE=DE=CD,
∴AB=AE+BE=AC+CD.
拓展练习
比较三角形三边的垂直平分线和三条角平分线的性质定理
三边垂直平分线
三条角平分线
三角形
锐角三角形
交于三角形内一点
交于三角形内一点
钝角三角形
交于三角形外一点
直角三角形
交于斜边的中点
交点性质
到三角形三个顶点的距离相等
到三角形三边的距离相等
课堂小结
课堂小结
角平分线上的点到角两边的距离相等.
在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.
(一)角平分线的性质定理
(二)角平分线的判定定理
三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.
(三)三角形角平分线的性质定理
https://www.21cnjy.com/help/help_extract.php
数学教学PPT
北师大版
八年级下
三
角
形
的
证
明
角平分线
还记得角平分线上的点有什么性质吗?你是怎样得到的?
角平分线上的点到角两边的距离相等.
温故导入
2
1
E
D
C
P
O
B
A
已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D、E.
求证:PD=PE.
证明:∵∠1=∠2,OP=OP,∠PDO=∠PEO=90°,
∴△PDO≌△PEO(AAS).
∴PD=PE(全等三角形的对应边相等)
2
1
E
D
C
P
O
B
A
小试牛刀
如果有一个点到角两边的距离相等,那么这个点必在这个角的平分线上.
你能写出这个定理的逆命题吗?
这个命题是假命题.角平分线是角内部的一条射线,而角的外部也存在到角两边距离相等的点.
角平分线性质定理的逆命题:在一个角的内部且到角的两边距离相等的点,在这个角的角平分线上.
这是一个真命题吗?
小试牛刀
已知:在∠AOB内部有一点P,且PD⊥OA,PE⊥OB,D、E为垂足且PD=PE,求证:点P在∠AOB的角平分线上.
证明:∵PD⊥OA,PE⊥OB,
∴∠PDO=∠
PEO=90°;
在Rt△ODP和Rt△OEP中,OP=OP,PD=PE
∴Rt△ODP
≌
Rt△OEP(HL).
∴∠1=∠2(全等三角形对应角相等).
2
1
E
D
C
P
O
B
A
大放异彩
解:
∵DE
⊥
AB,DF
⊥
AC,垂足分别为E,
F,且DE=DF,
∴AD平分∠BAC(在一个角的内部,到角的
E
两边距
离相等的点在这个角的平分线上).
又∵
∠BAC=60°,
∴
∠BAD=30°.
在Rt
△
ADE中,
∠AED=90°,AD=10,
∴DE=
2
AD=
2
×10=5(在直角三角形中,
如果一个锐角等
于30°,那么它所对的直角
边等于斜边的一半).
大放异彩
例题:在
△ABC
中,∠
BAC
=
60°,点
D
在
BC
上,AD
=
10,DE⊥AB,DF⊥AC,垂足分别为
E,F,且
DE
=
DF,求
DE
的长.
三角形的三个内角的角平分线,你发现了什么?
发现:三角形的三个内角的角平分线交于一点.这一点到三角形三边的距离相等.
仔细思考
剪一个三角形纸片,通过折叠找出每个角的角平分线,观察这三条角平分线,你是否发现同样的结论?与同伴交流.
D
F
E
M
N
C
B
A
P
仔细思考
D
E
F
M
N
C
B
A
P
证明:三角形三条角平分线相交于一点.
已知:如图,设△ABC的角平分线.BM、CN相交于点P,求证:P点在∠BAC的角平分线上.
证明:过P点作PD⊥AB,PF⊥AC,PE⊥BC,
其中D、E、F是垂足
∵BM是△ABC的角平分线,点P在BM上∴PD=PE
同理:PE=PF.∴PD=PF.∴点P在∠BAC的平分线上
∴△ABC的三条角平分线相交于点P.
探索求证
如图:直线L1、L2、L3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可选择的地址有几处?
满足条件共4个
P
1
P
l
3
l
2
1
l
C
B
A
拓展创新
[例1]如图,在△ABC中.AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)已知CD=4
cm,求AC的长;(2)求证:AB=AC+CD.
D
A
B
E
C
(1)解:∵AD是△ABC的角平分线,∠C=90°,DE⊥AB
∴DE=CD=4cm;∵AC=BC
∴∠B=∠BAC(等边对等角)
∵∠C=90°,∴∠B=1/2×90°=45°.
∴∠BDE=90°—45°=45°.∴BE=DE(等角对等边).
在等腰直角三角形BDE中(勾股定理)∴AC=BC=CD+BD=(4+4)cm.
拓展练习
[例1]如图,在△ABC中.AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)已知CD=4
cm,求AC的长;(2)求证:AB=AC+CD.
D
A
B
E
C
(2)证明:由(1)的求解过程可知,
Rt△ACD≌Rt△AED(HL)
∴AC=AE.
∵BE=DE=CD,
∴AB=AE+BE=AC+CD.
拓展练习
比较三角形三边的垂直平分线和三条角平分线的性质定理
三边垂直平分线
三条角平分线
三角形
锐角三角形
交于三角形内一点
交于三角形内一点
钝角三角形
交于三角形外一点
直角三角形
交于斜边的中点
交点性质
到三角形三个顶点的距离相等
到三角形三边的距离相等
课堂小结
课堂小结
角平分线上的点到角两边的距离相等.
在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.
(一)角平分线的性质定理
(二)角平分线的判定定理
三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.
(三)三角形角平分线的性质定理
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
