2.1 多边形 第2课时 多边形的外角和 课件(共23张PPT)
文档属性
| 名称 | 2.1 多边形 第2课时 多边形的外角和 课件(共23张PPT) |

|
|
| 格式 | rar | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 15:49:06 | ||
图片预览







文档简介
(共23张PPT)
多边形的外角和
第2章
四边形
湘教版·八年级下册
上课课件
学习目标
【知识与技能】
1.了解多边形的外角定义,并能准确找出多边形的外角.
2.掌握多边形的外角和公式,利用内角和与外角和公式解决实际问题.
【过程与方法】
1.经历探索多边形的外角和公式的过程,进一步发展学生的合情推理意识,主动探究的习惯,进一步体会数学与现实生活的紧密联系.
2.探索并了解多边形的外角和公式,进一步发展学生的说理和简单推理的意识及能力.
【情感态度】
经历多边形外角和的探索过程,培养学生主动探索的习惯,通过对内角、外角之间的关系,体会知识之间的内在联系.
【教学重点】
多边形外角和公式及其应用
【教学难点】
多边形外角和公式的推导
内角
?
多边形的内角的一边与另一边的反向延长线所组成的角叫作这个多边形的一个_____.
外角
∠EDF是五边形
ABCDE
的一个外角.
在多边形的每个顶点处取一个外角,它们的和叫作这个多边形的_______.
外角和
探索新知
我们已经知道三角形的外角和为
360°,那么四边形的外角和为多少度呢?
如图,在四边形ABCD的每一个顶点处取一个外角,如∠1,∠2,∠3,∠4.
∴
∠1
+∠2
+∠3
+∠4
=
4
×
180°
-
360°
=
360°.
∵
∠1
+∠DAB
=
180°,∠2
+∠ABC
=
180°,
∠3
+∠BCD
=
180°,
∠4
+∠ADC
=
180°,
又
∠DAB
+∠ABC
+∠BCD
+∠ADC
=
360°,
∴
四边形的外角和为360°.
三角形的外角和是
360°,四边形的外角和是360°,n
边形(
n
为不小于
3
的任意整数)的外角和都是
360°吗?n
边形的外角和与边数有关系吗?
五边形
1
2
3
4
5
5
个外角与跟它相邻的内角之和加起来是__________.
5×180°
五边形的内角和是____________.
(5-2)×180°
五边形的外角和是
___________________________.
5×180°-(5-2)×180°=
360°
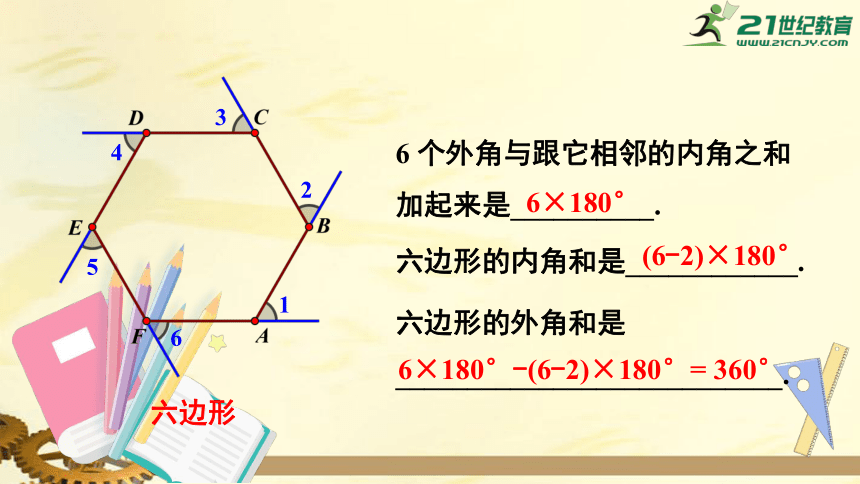
六边形
1
2
3
4
5
6
6
个外角与跟它相邻的内角之和加起来是__________.
6×180°
六边形的内角和是____________.
(6-2)×180°
六边形的外角和是
___________________________.
6×180°-(6-2)×180°=
360°
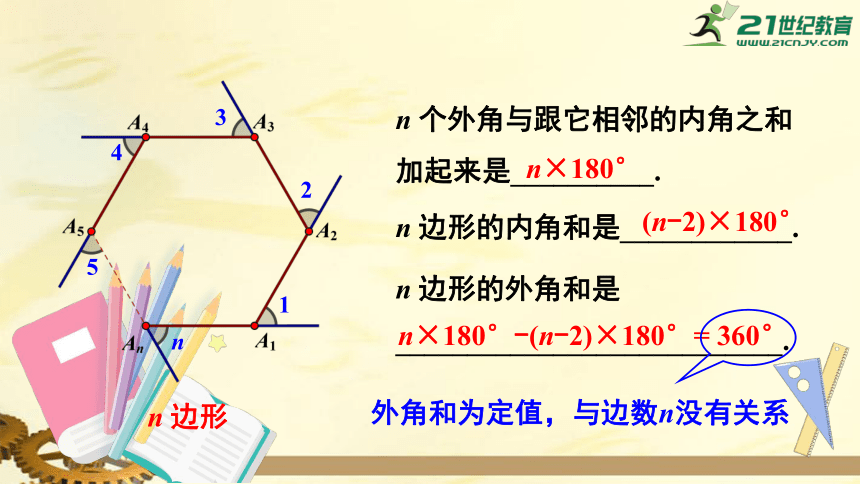
n
边形
1
2
3
4
5
n
n
个外角与跟它相邻的内角之和加起来是__________.
n×180°
n
边形的内角和是____________.
(n-2)×180°
n
边形的外角和是
___________________________.
n×180°-(n-2)×180°=
360°
外角和为定值,与边数n没有关系
图形
边数
多边形的外角和
三边形
3
四边形
4
五边形
5
六边形
6
…
…
n边形
n
3×180°-(3-2)×180°=
360°
4×180°-(4-2)×180°=
360°
5×180°-(5-2)×180°=
360°
6×180°-(6-2)×180°=
360°
n×180°-(n-2)×180°=
360°
一个多边形的内角和等于它外角和
的
5
倍,它是几边形?
解
设多边形的边数为
n,
则它的内角和等于
(n-2)·
180°.
由题意得
(n-2)·
180°=
5×360°,
解得
n
=
12.
因此这个多边形是十二边形.
【教材P37】
为什么自行车的三角架要做成三角形,做成四边形行吗?
三角形具有稳定性,
那么四边形呢?用
4
根木条钉成如图的木框,随意扭转四边形的边,它的形状会发生变化吗?
点击打开
我们发现,四边形的边长不变,但它的形状改变了,这说明四边形具有不稳定性.
在实际生活中,我们经常利用四边形的不稳定性.
有时又要克服四边形的不稳定性.
练习
【教材P38】
一个多边形的每一个外角都等于
45°,这个多边形
是几边形?它的每一个内角是多少度?
解
360°÷45°
=
8
内角和为
(8-2)×180°=
1080°
1080°÷8
=
135°
答:这个多边形是8边形,每一个内角是135°.
2.
如图,求图中
x
的值.
解
3x°+
90°+90°=
360°
x
=
60°
【教材P38】
3.
举出日常生活中利用四边形不稳定性的一些例子.
【教材P38】
伸缩晾衣杆
衣架
随堂练习
如图,在五边形
ABCDE
中,
AB
∥CD
,∠1,∠2,∠3
分别是与∠BAE,∠AED
,∠EDC
相邻的外角,
则
∠1+∠2+∠3等于(
)
A.
90°
B.
180°
C.
210°
D.
270°
B
2.
如图,工人师傅做了一个长方形窗框ABCD
,E,F,G,H
分别是四条边上的中点,为了使它稳固,需要在窗框上
钉一根木条,这根木条不应钉在(
)
A.
A,C两点之间
B.
E,G两点之间
C.
B,F两点之间
D.
G,H两点之间
B
3.
多边形的所有内角与某一外角的度数总和为
1350°,
那么这个多边形的边数是多少?
解:
设边数为
n,
外角为
x°,
则
x°+
(n-2)×180°=1350°,
∴
x°=1350°-180°(n-2).
∵
0°<
x°<180°,
∴
0<1350°-(n-2)×180°<180°
解得
.
∵
n
为整数
,
∴n
=
9.
∴
这个多边形的边数是
9.
课堂小结
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
多边形的外角和
第2章
四边形
湘教版·八年级下册
上课课件
学习目标
【知识与技能】
1.了解多边形的外角定义,并能准确找出多边形的外角.
2.掌握多边形的外角和公式,利用内角和与外角和公式解决实际问题.
【过程与方法】
1.经历探索多边形的外角和公式的过程,进一步发展学生的合情推理意识,主动探究的习惯,进一步体会数学与现实生活的紧密联系.
2.探索并了解多边形的外角和公式,进一步发展学生的说理和简单推理的意识及能力.
【情感态度】
经历多边形外角和的探索过程,培养学生主动探索的习惯,通过对内角、外角之间的关系,体会知识之间的内在联系.
【教学重点】
多边形外角和公式及其应用
【教学难点】
多边形外角和公式的推导
内角
?
多边形的内角的一边与另一边的反向延长线所组成的角叫作这个多边形的一个_____.
外角
∠EDF是五边形
ABCDE
的一个外角.
在多边形的每个顶点处取一个外角,它们的和叫作这个多边形的_______.
外角和
探索新知
我们已经知道三角形的外角和为
360°,那么四边形的外角和为多少度呢?
如图,在四边形ABCD的每一个顶点处取一个外角,如∠1,∠2,∠3,∠4.
∴
∠1
+∠2
+∠3
+∠4
=
4
×
180°
-
360°
=
360°.
∵
∠1
+∠DAB
=
180°,∠2
+∠ABC
=
180°,
∠3
+∠BCD
=
180°,
∠4
+∠ADC
=
180°,
又
∠DAB
+∠ABC
+∠BCD
+∠ADC
=
360°,
∴
四边形的外角和为360°.
三角形的外角和是
360°,四边形的外角和是360°,n
边形(
n
为不小于
3
的任意整数)的外角和都是
360°吗?n
边形的外角和与边数有关系吗?
五边形
1
2
3
4
5
5
个外角与跟它相邻的内角之和加起来是__________.
5×180°
五边形的内角和是____________.
(5-2)×180°
五边形的外角和是
___________________________.
5×180°-(5-2)×180°=
360°
六边形
1
2
3
4
5
6
6
个外角与跟它相邻的内角之和加起来是__________.
6×180°
六边形的内角和是____________.
(6-2)×180°
六边形的外角和是
___________________________.
6×180°-(6-2)×180°=
360°
n
边形
1
2
3
4
5
n
n
个外角与跟它相邻的内角之和加起来是__________.
n×180°
n
边形的内角和是____________.
(n-2)×180°
n
边形的外角和是
___________________________.
n×180°-(n-2)×180°=
360°
外角和为定值,与边数n没有关系
图形
边数
多边形的外角和
三边形
3
四边形
4
五边形
5
六边形
6
…
…
n边形
n
3×180°-(3-2)×180°=
360°
4×180°-(4-2)×180°=
360°
5×180°-(5-2)×180°=
360°
6×180°-(6-2)×180°=
360°
n×180°-(n-2)×180°=
360°
一个多边形的内角和等于它外角和
的
5
倍,它是几边形?
解
设多边形的边数为
n,
则它的内角和等于
(n-2)·
180°.
由题意得
(n-2)·
180°=
5×360°,
解得
n
=
12.
因此这个多边形是十二边形.
【教材P37】
为什么自行车的三角架要做成三角形,做成四边形行吗?
三角形具有稳定性,
那么四边形呢?用
4
根木条钉成如图的木框,随意扭转四边形的边,它的形状会发生变化吗?
点击打开
我们发现,四边形的边长不变,但它的形状改变了,这说明四边形具有不稳定性.
在实际生活中,我们经常利用四边形的不稳定性.
有时又要克服四边形的不稳定性.
练习
【教材P38】
一个多边形的每一个外角都等于
45°,这个多边形
是几边形?它的每一个内角是多少度?
解
360°÷45°
=
8
内角和为
(8-2)×180°=
1080°
1080°÷8
=
135°
答:这个多边形是8边形,每一个内角是135°.
2.
如图,求图中
x
的值.
解
3x°+
90°+90°=
360°
x
=
60°
【教材P38】
3.
举出日常生活中利用四边形不稳定性的一些例子.
【教材P38】
伸缩晾衣杆
衣架
随堂练习
如图,在五边形
ABCDE
中,
AB
∥CD
,∠1,∠2,∠3
分别是与∠BAE,∠AED
,∠EDC
相邻的外角,
则
∠1+∠2+∠3等于(
)
A.
90°
B.
180°
C.
210°
D.
270°
B
2.
如图,工人师傅做了一个长方形窗框ABCD
,E,F,G,H
分别是四条边上的中点,为了使它稳固,需要在窗框上
钉一根木条,这根木条不应钉在(
)
A.
A,C两点之间
B.
E,G两点之间
C.
B,F两点之间
D.
G,H两点之间
B
3.
多边形的所有内角与某一外角的度数总和为
1350°,
那么这个多边形的边数是多少?
解:
设边数为
n,
外角为
x°,
则
x°+
(n-2)×180°=1350°,
∴
x°=1350°-180°(n-2).
∵
0°<
x°<180°,
∴
0<1350°-(n-2)×180°<180°
解得
.
∵
n
为整数
,
∴n
=
9.
∴
这个多边形的边数是
9.
课堂小结
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
