2.2.2 平行四边形的判定(第1课时) 平行四边形的判定定理1,2 课件(共20张PPT)
文档属性
| 名称 | 2.2.2 平行四边形的判定(第1课时) 平行四边形的判定定理1,2 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 00:00:00 | ||
图片预览


文档简介
(共20张PPT)
平行四边形的判定定理1,2
第2章
四边形
湘教版·八年级下册
上课课件
学习目标
【知识与技能】
1.经历探究平行四边形判定方法的过程,掌握平行四边形的判定方法.
2.会判定一个四边形是不是平行四边形.
【过程与方法】
经历“观察——猜想——验证——说明——建模”探索过程和思维过程,丰富学生从事数学活动的经历,感受数学思考过程的条理性及解决问题策略的多样性.
【情感态度】
在观察分析探究问题过程中发现主动探索、独立思考的习惯.
【教学重点】
探索平行四边形的两种判别方法.
【教学难点】
平行四边形的判别方法的理解和应用.
新课导入
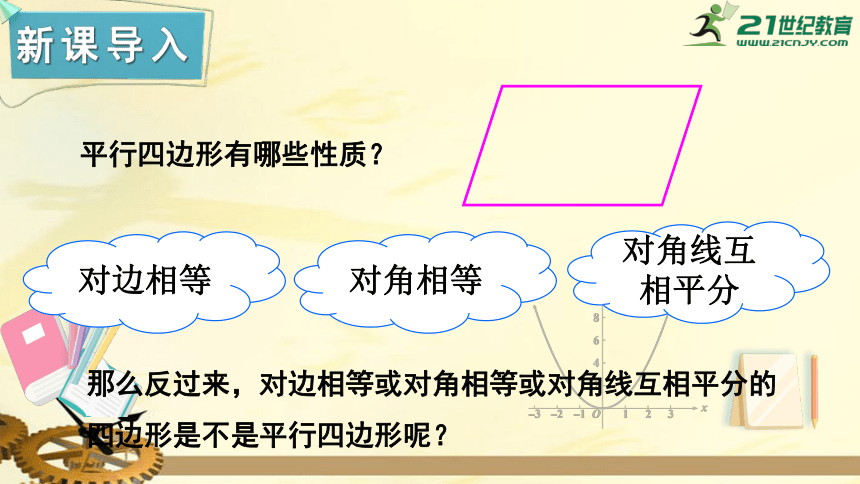
平行四边形有哪些性质?
对边相等
对角相等
对角线互相平分
那么反过来,对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢?
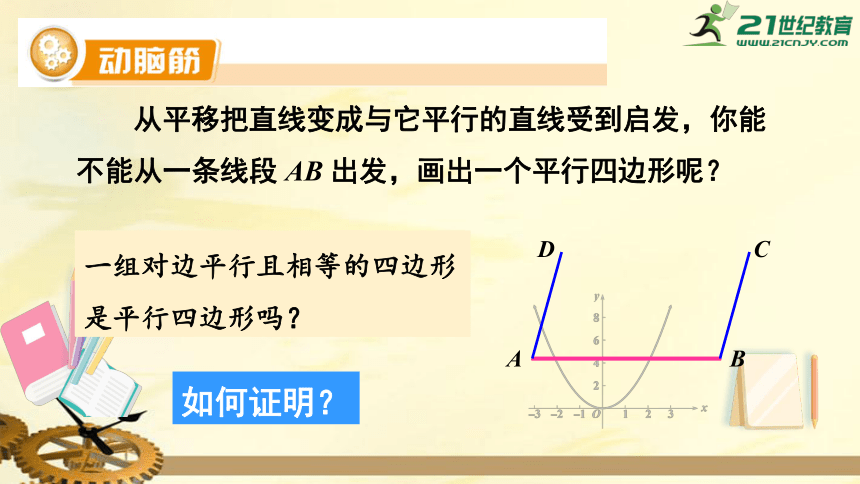
从平移把直线变成与它平行的直线受到启发,你能不能从一条线段
AB
出发,画出一个平行四边形呢?
A
B
D
C
一组对边平行且相等的四边形是平行四边形吗?
如何证明?
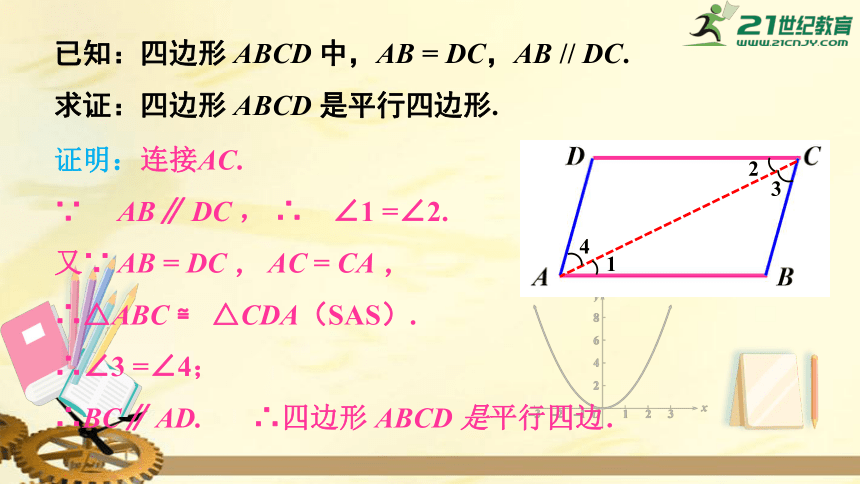
已知:四边形
ABCD
中,AB
=
DC,AB
//
DC.
求证:四边形
ABCD
是平行四边形.
证明:连接AC.
∵
AB∥
DC
,
∴ ∠1
=∠2.
又∵
AB
=
DC
,
AC
=
CA
,
∴△ABC
≌
△CDA(SAS).
∴∠3
=∠4;
∴BC∥
AD.
∴四边形
ABCD
是平行四边.
1
2
3
4
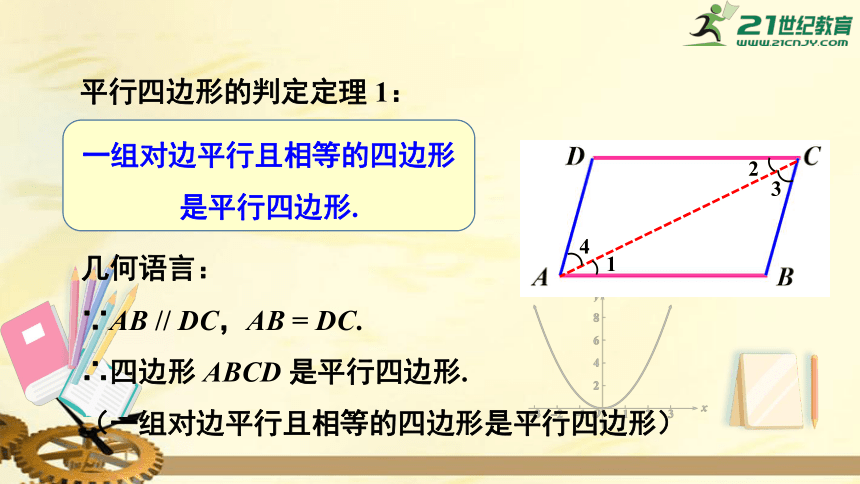
平行四边形的判定定理
1:
1
2
3
4
一组对边平行且相等的四边形是平行四边形.
几何语言:
∵AB
//
DC,AB
=
DC.
∴四边形
ABCD
是平行四边形.
(一组对边平行且相等的四边形是平行四边形)
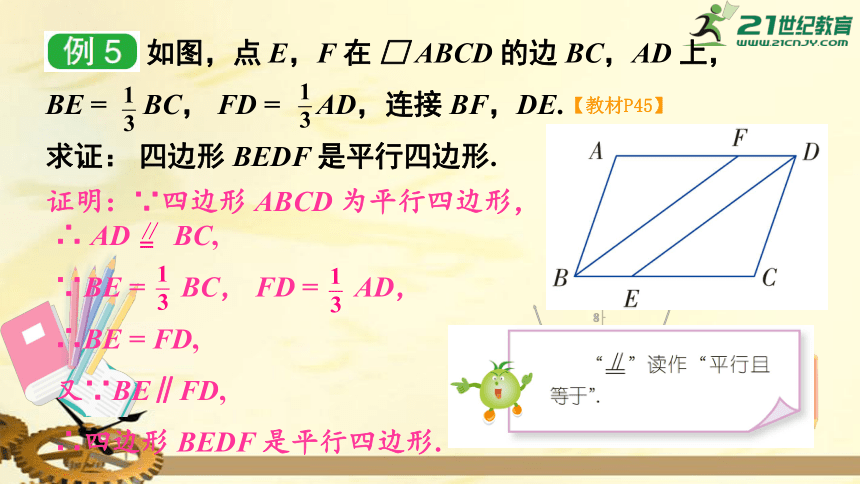
如图,点
E,F
在
□
ABCD
的边
BC,AD
上,
BE
=
BC,
FD
=
AD,连接
BF,DE.
求证:
四边形
BEDF
是平行四边形.
证明:∵四边形
ABCD
为平行四边形,
∴
AD
BC,
∵BE
=
BC,
FD
=
AD,
∴BE
=
FD,
又∵BE∥FD,
∴四边形
BEDF
是平行四边形.
【教材P45】
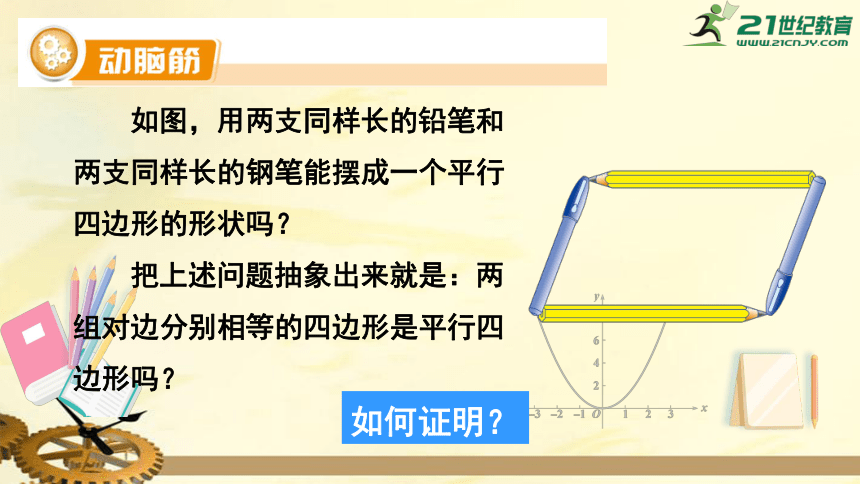
如图,用两支同样长的铅笔和两支同样长的钢笔能摆成一个平行四边形的形状吗?
把上述问题抽象出来就是:两组对边分别相等的四边形是平行四边形吗?
如何证明?
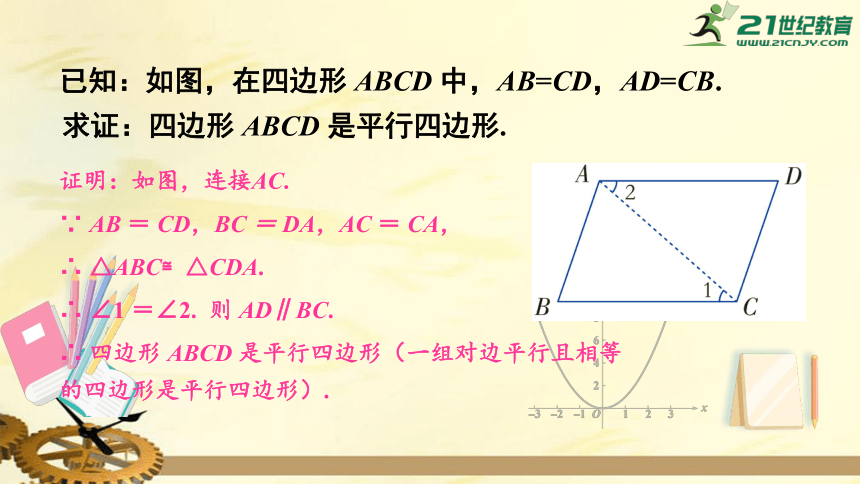
证明:如图,连接AC.
∵
AB
=
CD,BC
=
DA,AC
=
CA,
∴
△ABC≌△CDA.
∴
∠1
=∠2.
则
AD∥BC.
∴
四边形
ABCD
是平行四边形(一组对边平行且相等的四边形是平行四边形).
已知:如图,在四边形
ABCD
中,AB=CD,AD=CB.
求证:四边形
ABCD
是平行四边形.
平行四边形的判定定理
2:
两组对边分别相等的四边形是平行四边形.
几何语言
∵AB=CD,AD=BC.
∴四边形
ABCD
是平行四边形.
(两组对边分别相等的四边形是平行四边形)
如图,在四边形
ABCD
中,△ABC
≌△
CDA.
求证:四边形
ABCD
是平行四边形.
证明∵
△ABC
≌
△CDA,
∴
AB
=
CD,
BC
=
DA.
∴
四边形
ABCD
是平行四边形.
【教材P46】
练习
1.
如图,在
□
ABCD
中,AE=
CF
.
求证:
四边形
EBFD
是平行四边形.
【教材P46】
证明
∵四边形ABCD是平行四边形,
∴
AB
∥
CD
,
AB
=
CD.
又∵AE
=
CF.
∴BE
=
DF,
BE
∥
DF
∴四边形
EBFD
是平行四边形.
2.如图,在四边形
ABCD
中,AD
=
BC,AB
=DC,E,F
分别是边
BC,AD
上的中点.
找出图中所有的平行四边形,并说明理由.
【教材P46】
平行四边形有
ABCD
,
ABEF
,
CDFE.
理由
∵
AD
=
BC,AB
=DC.
∴四边形
ABCD
是平行四边形.
∵E,F是中点,∴AF
=
BE,
FD
=
CE.
∴四边形ABEF,
CDFE是平行四边形.
随堂练习
1.
如图,在四边形
ABCD
中,E
是
BC
边上的中点,连接
DE
并延长,交
AB
的延长线于点F,
AB
=BF.若要添加一个条件,使四边形
ABCD
是平行四边形,则下面四个条件中可选择的是(
)
A.AD
=
BC
B.CD
=
BF
C.∠A
=∠C
D.∠F=∠CDE
D
2.
(咸宁中考)如图,
点
B,
E,
C,
F
在一条直线上
,
AB=DF,
AC=DE,
BE=FC.
(1)求证:△ABC≌△DFE;
(2)连接
AF,
BD,
求证:四边形
ABDF
是平行四边形.
证明:(1)∵BE
=
FC,
∴BC=
FE.
在△ABC
和△DFE
中,
AB=DF,
AC=DE,
BC=
FE,
∴△ABC≌△DFE
(
SSS
).
2.
(咸宁中考)如图,
点
B,
E,
C,
F
在一条直线上
,
AB=DF,
AC=DE,
BE=FC.
(1)求证:△ABC≌△DFE;
(2)连接
AF,
BD,
求证:四边形
ABDF
是平行四边形.
证明:(2)由(1)知△ABC
≌
△DFE,
∴∠ABC=∠DFE.∴AB∥DF.
又∵AB=DF,∴四边形
ABDF
是平行四边形.
平行四边形的判定定理
1:
课堂小结
一组对边平行且相等的四边形是平行四边形.
平行四边形的判定定理
2:
两组对边分别相等的四边形是平行四边形.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
平行四边形的判定定理1,2
第2章
四边形
湘教版·八年级下册
上课课件
学习目标
【知识与技能】
1.经历探究平行四边形判定方法的过程,掌握平行四边形的判定方法.
2.会判定一个四边形是不是平行四边形.
【过程与方法】
经历“观察——猜想——验证——说明——建模”探索过程和思维过程,丰富学生从事数学活动的经历,感受数学思考过程的条理性及解决问题策略的多样性.
【情感态度】
在观察分析探究问题过程中发现主动探索、独立思考的习惯.
【教学重点】
探索平行四边形的两种判别方法.
【教学难点】
平行四边形的判别方法的理解和应用.
新课导入
平行四边形有哪些性质?
对边相等
对角相等
对角线互相平分
那么反过来,对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢?
从平移把直线变成与它平行的直线受到启发,你能不能从一条线段
AB
出发,画出一个平行四边形呢?
A
B
D
C
一组对边平行且相等的四边形是平行四边形吗?
如何证明?
已知:四边形
ABCD
中,AB
=
DC,AB
//
DC.
求证:四边形
ABCD
是平行四边形.
证明:连接AC.
∵
AB∥
DC
,
∴ ∠1
=∠2.
又∵
AB
=
DC
,
AC
=
CA
,
∴△ABC
≌
△CDA(SAS).
∴∠3
=∠4;
∴BC∥
AD.
∴四边形
ABCD
是平行四边.
1
2
3
4
平行四边形的判定定理
1:
1
2
3
4
一组对边平行且相等的四边形是平行四边形.
几何语言:
∵AB
//
DC,AB
=
DC.
∴四边形
ABCD
是平行四边形.
(一组对边平行且相等的四边形是平行四边形)
如图,点
E,F
在
□
ABCD
的边
BC,AD
上,
BE
=
BC,
FD
=
AD,连接
BF,DE.
求证:
四边形
BEDF
是平行四边形.
证明:∵四边形
ABCD
为平行四边形,
∴
AD
BC,
∵BE
=
BC,
FD
=
AD,
∴BE
=
FD,
又∵BE∥FD,
∴四边形
BEDF
是平行四边形.
【教材P45】
如图,用两支同样长的铅笔和两支同样长的钢笔能摆成一个平行四边形的形状吗?
把上述问题抽象出来就是:两组对边分别相等的四边形是平行四边形吗?
如何证明?
证明:如图,连接AC.
∵
AB
=
CD,BC
=
DA,AC
=
CA,
∴
△ABC≌△CDA.
∴
∠1
=∠2.
则
AD∥BC.
∴
四边形
ABCD
是平行四边形(一组对边平行且相等的四边形是平行四边形).
已知:如图,在四边形
ABCD
中,AB=CD,AD=CB.
求证:四边形
ABCD
是平行四边形.
平行四边形的判定定理
2:
两组对边分别相等的四边形是平行四边形.
几何语言
∵AB=CD,AD=BC.
∴四边形
ABCD
是平行四边形.
(两组对边分别相等的四边形是平行四边形)
如图,在四边形
ABCD
中,△ABC
≌△
CDA.
求证:四边形
ABCD
是平行四边形.
证明∵
△ABC
≌
△CDA,
∴
AB
=
CD,
BC
=
DA.
∴
四边形
ABCD
是平行四边形.
【教材P46】
练习
1.
如图,在
□
ABCD
中,AE=
CF
.
求证:
四边形
EBFD
是平行四边形.
【教材P46】
证明
∵四边形ABCD是平行四边形,
∴
AB
∥
CD
,
AB
=
CD.
又∵AE
=
CF.
∴BE
=
DF,
BE
∥
DF
∴四边形
EBFD
是平行四边形.
2.如图,在四边形
ABCD
中,AD
=
BC,AB
=DC,E,F
分别是边
BC,AD
上的中点.
找出图中所有的平行四边形,并说明理由.
【教材P46】
平行四边形有
ABCD
,
ABEF
,
CDFE.
理由
∵
AD
=
BC,AB
=DC.
∴四边形
ABCD
是平行四边形.
∵E,F是中点,∴AF
=
BE,
FD
=
CE.
∴四边形ABEF,
CDFE是平行四边形.
随堂练习
1.
如图,在四边形
ABCD
中,E
是
BC
边上的中点,连接
DE
并延长,交
AB
的延长线于点F,
AB
=BF.若要添加一个条件,使四边形
ABCD
是平行四边形,则下面四个条件中可选择的是(
)
A.AD
=
BC
B.CD
=
BF
C.∠A
=∠C
D.∠F=∠CDE
D
2.
(咸宁中考)如图,
点
B,
E,
C,
F
在一条直线上
,
AB=DF,
AC=DE,
BE=FC.
(1)求证:△ABC≌△DFE;
(2)连接
AF,
BD,
求证:四边形
ABDF
是平行四边形.
证明:(1)∵BE
=
FC,
∴BC=
FE.
在△ABC
和△DFE
中,
AB=DF,
AC=DE,
BC=
FE,
∴△ABC≌△DFE
(
SSS
).
2.
(咸宁中考)如图,
点
B,
E,
C,
F
在一条直线上
,
AB=DF,
AC=DE,
BE=FC.
(1)求证:△ABC≌△DFE;
(2)连接
AF,
BD,
求证:四边形
ABDF
是平行四边形.
证明:(2)由(1)知△ABC
≌
△DFE,
∴∠ABC=∠DFE.∴AB∥DF.
又∵AB=DF,∴四边形
ABDF
是平行四边形.
平行四边形的判定定理
1:
课堂小结
一组对边平行且相等的四边形是平行四边形.
平行四边形的判定定理
2:
两组对边分别相等的四边形是平行四边形.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
