2.2.2 平行四边形的判定(第2课时) 平行四边形的判定定理3 课件(共22张PPT)
文档属性
| 名称 | 2.2.2 平行四边形的判定(第2课时) 平行四边形的判定定理3 课件(共22张PPT) |

|
|
| 格式 | rar | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
平行四边形的判定定理
3
第2章
四边形
湘教版·八年级下册
上课课件
学习目标
【知识与技能】
使学生掌握用“对角线互相平分的四边形是平行四边形”这一判定定理,会用这些定理进行有关的论证和计算;理解“两组对角分别相等的四边形是平行四边形”这一判定定理,会用这些定理进行有关的论证和计算.
【过程与方法】
经历观察、归纳等教学活动过程,培养学生的合作精神和有条理的思考和探究的能力.
【情感态度】
通过生动有趣的数学活动,让学生主动探索、敢于表达、乐于合作交流,进一步体验数学在生活中的应用,体验因学习而带来的快乐.
【教学重点】
理解掌握“对角线互相平分的四边形是平行四边形,两组对角分别相等的四边形是平行四边形”这一判定定理.
【教学难点】
判定定理的证明方法及运用.
新课导入
要判定一个四边形是平行四边形,我们已经从边的角度进行了研究,说一说有哪几种方法?
一组对边平行且相等的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
新课导入
要判定一个四边形是平行四边形,我们已经从边的角度进行了研究,说一说有哪几种方法?
除了这些方法外,还有其他方法吗?
观察图,从“平行四边形对角线互相平分”这一性质受到启发,你能画出一个平行四边形吗?
已知:四边形
ABCD
中,OA
=
OC,OB
=
OD.
求证:四边形
ABCD
是平行四边形.
证明:在四边形ABCD
中,OA
=
OC,OB
=
OD,
又∠AOB
=∠COD,
∴
△AOB≌△COD.
∴
AB
=
CD,
∠ABO
=∠CDO.
从而
AB∥CD
.
∴
四边形
ABCD
是平行四边形.
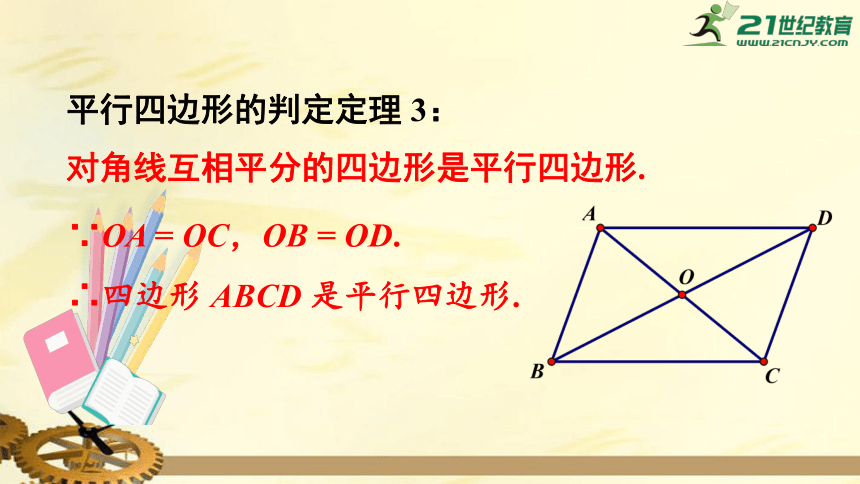
平行四边形的判定定理
3:
对角线互相平分的四边形是平行四边形.
∵OA
=
OC,OB
=
OD.
∴四边形
ABCD
是平行四边形.
已知:如图,□
ABCD
的对角线
AC,BD
相交于点
O,点
E、F
在
BD
上,且
OE
=
OF.
求证:四边形
AECF
也是平行四边形.
【教材P47】
证明
∵
四边形
ABCD
为平行四边形,
∴
OA
=
OC.
又∵
OE
=
OF,
∴
四边形
AECF
是平行四边形.
已知:如图,在四边形
ABCD
中,
∠A
=
∠C,
∠B
=
∠D.
求证:四边形
ABCD
是平行四边形.
【教材P47】
证明∵
∠A
=∠C,
∠B
=∠D,
∠A
+∠B
+∠C
+∠D
=
360°,
∴
∠A
+∠B
=
=
180°.
∴
AD∥BC,同理,AB∥DC.
∴
四边形
ABCD
是平行四边形.
两组对角分别相等的四边形是平行四边形.
两组邻边分别相等的四边形一定是平行四边形吗?
如果是,请说明理由;如果不是,请举出反例.
不一定是平行四边形.
2.
一组对边相等,另一组对边平行的四边形一定是平行四
边形吗?如果是,请说明理由;如果不是,请举出反例.
不一定是平行四边形.
说一说,平行四边形的判定方法.
已知条件
选择判定方法
两组对边分别平行
两组对边分别平行的四边形是平行四边形;
一组对边平行且相等
一组对边平行且相等的四边形是平行四边形;
两组对边分别相等
两组对边分别相等的四边形是平行四边形;
对角线互相平分
对角线互相平分的四边形是平行四边形;
两组对角分别相等
两组对角分别相等的四边形是平行四边形.
练习
1.如图,把△
ABC
的中线延长至
E,使得
DE
=
AD,连接
EB
,
EC.
求证:四边形
ABEC
是平行四边形.
【教材P48】
证明:∵CD
=
DB,
AD
=
DE,
而对角线互相平分的四边形是平行四边形
∴四边形
ABEC
是平行四边形.
2.
如图,□
ABCD
的对角线相交于点
O,直线
MN
经过点
O,
分别与
AB,CD
交于点
M,N,连接
AN,CM.
求证:四边形
AMCN
是平行四边形.
【教材P48】
证明:
在△AMO和△CNO,
∵AO
=
CO,
∠AOM
=
∠CON(对顶角),
∠MAO
=
∠NCO,
∴△AMO≌△CNO(ASA).
∴MO
=
NO.
即AC
与
MN
互相平分,且是四边形
AMCN
的对角线,
∴四边形
AMCN
是平行四边形.
随堂练习
1.
下面给出了四边形
ABCD
中∠A
,∠B,∠C,∠D
的度数之比,
其中能判定四边形
ABCD
是平行四边形的是(
)
A.3∶4∶4∶3
B.2∶2∶3∶3
C.4∶3∶2∶1
D.4∶3∶4∶3
D
2.
如图,在
□
ABCD
中,E、F
分别是对角线
BD
上两点,且
BE
=
DF,要证明四边形
AECF
是平行四边形,最简捷的方法是根据_________________________________来证明.
对角线互相平分的四边形是平行四边形
3.
如图,△ABC
中,点
O
是
AC
边上的一个动点,过点
O
作直线
MN∥BC
交∠ACB
的平分线于点
E,交∠ACB
的外角平分线于点
F.
(1)
请说明
EO
=
FO.
(2)
当点
O
在
AC
上运动到何处时,四边形
AECF
是平行四边形?
并说明理由.
点击打开
4.如图,在
□
ABCD
中,AE⊥BD,CF⊥
BD,
垂足分别为点
E,F.
求证:
四边形
AECF
是平行四边形.
证明:
∵AE
⊥
BD
于点
E,CF⊥
BD
于点
F,
∴AE∥FC.
在
Rt△AEB
和
Rt△CFD
中,
∵AB
=
CD,∠ABE
=
∠CDF,
∠AEB
=
∠CFD,
∴
Rt
△AEB
≌
Rt
△CFD(AAS).
∴AE
=
CF.
∵AE∥FC,AE
=
CF,
∴四边形
AECF
是平行四边形.
课堂小结
平行四边形的判定方法.
已知条件
选择判定方法
两组对边分别平行
两组对边分别平行的四边形是平行四边形;
一组对边平行且相等
一组对边平行且相等的四边形是平行四边形;
两组对边分别相等
两组对边分别相等的四边形是平行四边形;
对角线互相平分
对角线互相平分的四边形是平行四边形;
两组对角分别相等
两组对角分别相等的四边形是平行四边形.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
平行四边形的判定定理
3
第2章
四边形
湘教版·八年级下册
上课课件
学习目标
【知识与技能】
使学生掌握用“对角线互相平分的四边形是平行四边形”这一判定定理,会用这些定理进行有关的论证和计算;理解“两组对角分别相等的四边形是平行四边形”这一判定定理,会用这些定理进行有关的论证和计算.
【过程与方法】
经历观察、归纳等教学活动过程,培养学生的合作精神和有条理的思考和探究的能力.
【情感态度】
通过生动有趣的数学活动,让学生主动探索、敢于表达、乐于合作交流,进一步体验数学在生活中的应用,体验因学习而带来的快乐.
【教学重点】
理解掌握“对角线互相平分的四边形是平行四边形,两组对角分别相等的四边形是平行四边形”这一判定定理.
【教学难点】
判定定理的证明方法及运用.
新课导入
要判定一个四边形是平行四边形,我们已经从边的角度进行了研究,说一说有哪几种方法?
一组对边平行且相等的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
新课导入
要判定一个四边形是平行四边形,我们已经从边的角度进行了研究,说一说有哪几种方法?
除了这些方法外,还有其他方法吗?
观察图,从“平行四边形对角线互相平分”这一性质受到启发,你能画出一个平行四边形吗?
已知:四边形
ABCD
中,OA
=
OC,OB
=
OD.
求证:四边形
ABCD
是平行四边形.
证明:在四边形ABCD
中,OA
=
OC,OB
=
OD,
又∠AOB
=∠COD,
∴
△AOB≌△COD.
∴
AB
=
CD,
∠ABO
=∠CDO.
从而
AB∥CD
.
∴
四边形
ABCD
是平行四边形.
平行四边形的判定定理
3:
对角线互相平分的四边形是平行四边形.
∵OA
=
OC,OB
=
OD.
∴四边形
ABCD
是平行四边形.
已知:如图,□
ABCD
的对角线
AC,BD
相交于点
O,点
E、F
在
BD
上,且
OE
=
OF.
求证:四边形
AECF
也是平行四边形.
【教材P47】
证明
∵
四边形
ABCD
为平行四边形,
∴
OA
=
OC.
又∵
OE
=
OF,
∴
四边形
AECF
是平行四边形.
已知:如图,在四边形
ABCD
中,
∠A
=
∠C,
∠B
=
∠D.
求证:四边形
ABCD
是平行四边形.
【教材P47】
证明∵
∠A
=∠C,
∠B
=∠D,
∠A
+∠B
+∠C
+∠D
=
360°,
∴
∠A
+∠B
=
=
180°.
∴
AD∥BC,同理,AB∥DC.
∴
四边形
ABCD
是平行四边形.
两组对角分别相等的四边形是平行四边形.
两组邻边分别相等的四边形一定是平行四边形吗?
如果是,请说明理由;如果不是,请举出反例.
不一定是平行四边形.
2.
一组对边相等,另一组对边平行的四边形一定是平行四
边形吗?如果是,请说明理由;如果不是,请举出反例.
不一定是平行四边形.
说一说,平行四边形的判定方法.
已知条件
选择判定方法
两组对边分别平行
两组对边分别平行的四边形是平行四边形;
一组对边平行且相等
一组对边平行且相等的四边形是平行四边形;
两组对边分别相等
两组对边分别相等的四边形是平行四边形;
对角线互相平分
对角线互相平分的四边形是平行四边形;
两组对角分别相等
两组对角分别相等的四边形是平行四边形.
练习
1.如图,把△
ABC
的中线延长至
E,使得
DE
=
AD,连接
EB
,
EC.
求证:四边形
ABEC
是平行四边形.
【教材P48】
证明:∵CD
=
DB,
AD
=
DE,
而对角线互相平分的四边形是平行四边形
∴四边形
ABEC
是平行四边形.
2.
如图,□
ABCD
的对角线相交于点
O,直线
MN
经过点
O,
分别与
AB,CD
交于点
M,N,连接
AN,CM.
求证:四边形
AMCN
是平行四边形.
【教材P48】
证明:
在△AMO和△CNO,
∵AO
=
CO,
∠AOM
=
∠CON(对顶角),
∠MAO
=
∠NCO,
∴△AMO≌△CNO(ASA).
∴MO
=
NO.
即AC
与
MN
互相平分,且是四边形
AMCN
的对角线,
∴四边形
AMCN
是平行四边形.
随堂练习
1.
下面给出了四边形
ABCD
中∠A
,∠B,∠C,∠D
的度数之比,
其中能判定四边形
ABCD
是平行四边形的是(
)
A.3∶4∶4∶3
B.2∶2∶3∶3
C.4∶3∶2∶1
D.4∶3∶4∶3
D
2.
如图,在
□
ABCD
中,E、F
分别是对角线
BD
上两点,且
BE
=
DF,要证明四边形
AECF
是平行四边形,最简捷的方法是根据_________________________________来证明.
对角线互相平分的四边形是平行四边形
3.
如图,△ABC
中,点
O
是
AC
边上的一个动点,过点
O
作直线
MN∥BC
交∠ACB
的平分线于点
E,交∠ACB
的外角平分线于点
F.
(1)
请说明
EO
=
FO.
(2)
当点
O
在
AC
上运动到何处时,四边形
AECF
是平行四边形?
并说明理由.
点击打开
4.如图,在
□
ABCD
中,AE⊥BD,CF⊥
BD,
垂足分别为点
E,F.
求证:
四边形
AECF
是平行四边形.
证明:
∵AE
⊥
BD
于点
E,CF⊥
BD
于点
F,
∴AE∥FC.
在
Rt△AEB
和
Rt△CFD
中,
∵AB
=
CD,∠ABE
=
∠CDF,
∠AEB
=
∠CFD,
∴
Rt
△AEB
≌
Rt
△CFD(AAS).
∴AE
=
CF.
∵AE∥FC,AE
=
CF,
∴四边形
AECF
是平行四边形.
课堂小结
平行四边形的判定方法.
已知条件
选择判定方法
两组对边分别平行
两组对边分别平行的四边形是平行四边形;
一组对边平行且相等
一组对边平行且相等的四边形是平行四边形;
两组对边分别相等
两组对边分别相等的四边形是平行四边形;
对角线互相平分
对角线互相平分的四边形是平行四边形;
两组对角分别相等
两组对角分别相等的四边形是平行四边形.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
