2.3 中心对称和中心对称图形( 第1课时) 中心对称概念及性质 课件(共18张PPT)
文档属性
| 名称 | 2.3 中心对称和中心对称图形( 第1课时) 中心对称概念及性质 课件(共18张PPT) |

|
|
| 格式 | rar | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
中心对称概念及性质
第2章
四边形
湘教版·八年级下册
上课课件
学习目标
【知识与技能】
1.了解中心对称、对称中心和对称点的概念.
2.理解中心对称的性质.
3.掌握运用中心对称的性质作图的方法.
【过程与方法】
通过对中心对称的性质的探究及运用,初步学会从正反两方面去思考问题的数学思考方法,以及类比思想的应用.
【情感态度】
通过一系列探索活动,培养学生严谨的科学态度和探索的精神;经历数学知识融于生活实际的实习过程,体验数学学习的快乐.
【教学重点】
中心对称的概念;中心对称的性质;利用中心对称的性质进行作图.
【教学难点】
中心对称与轴对称的区别与联系,利用中心对称的性质准确作图.
新课导入
(1)把一个图案绕点
O
旋转
180°,你有什么发现?
点击打开
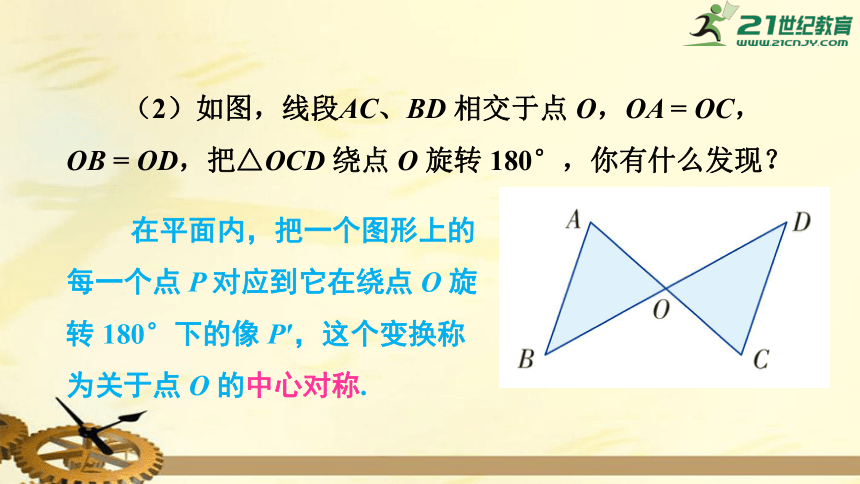
(2)如图,线段AC、BD
相交于点
O,OA
=
OC,OB
=
OD,把△OCD
绕点
O
旋转
180°,你有什么发现?
点击打开
在平面内,把一个图形上的每一个点
P
对应到它在绕点
O
旋转
180°下的像
P′,这个变换称为关于点
O
的中心对称.
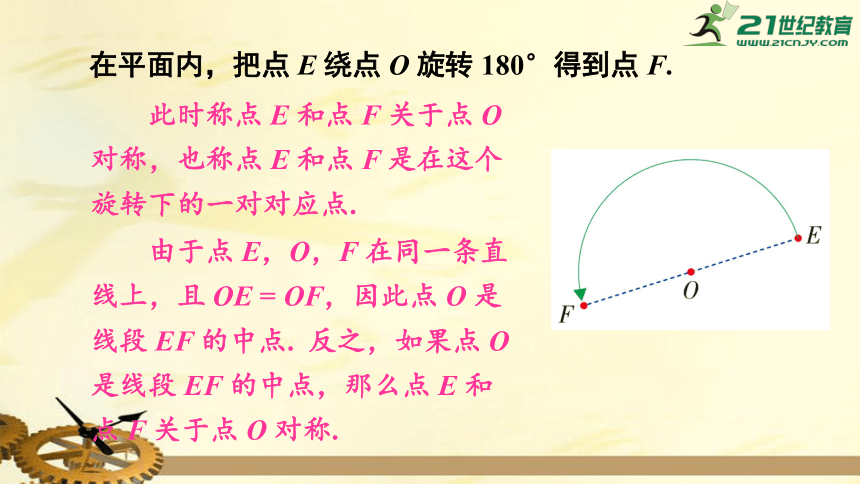
在平面内,把点
E
绕点
O
旋转
180°得到点
F.
点击打开
此时称点
E
和点
F
关于点
O
对称,也称点
E
和点
F
是在这个旋转下的一对对应点.
由于点
E,O,F
在同一条直线上,且
OE
=
OF,因此点
O
是线段
EF
的中点.
反之,如果点
O
是线段
EF
的中点,那么点
E
和点
F
关于点
O
对称.
点击打开
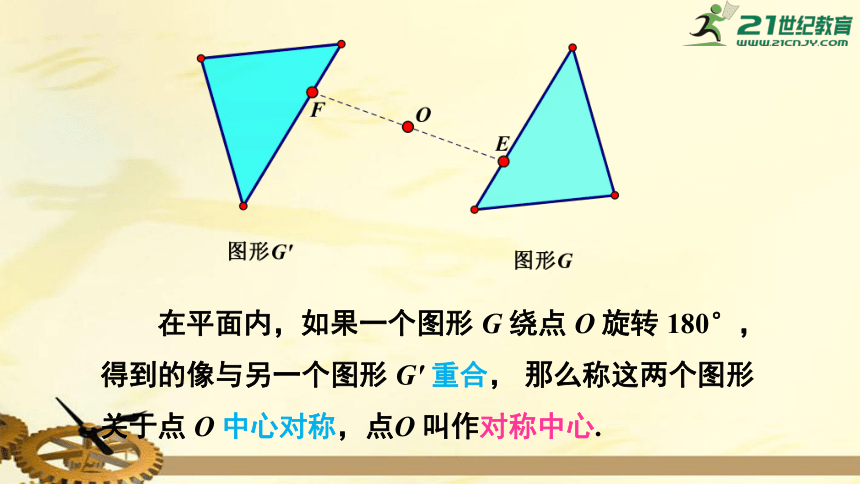
在平面内,如果一个图形
G
绕点
O
旋转
180°,得到的像与另一个图形
G′
重合,
那么称这两个图形关于点
O
中心对称,点O
叫作对称中心.
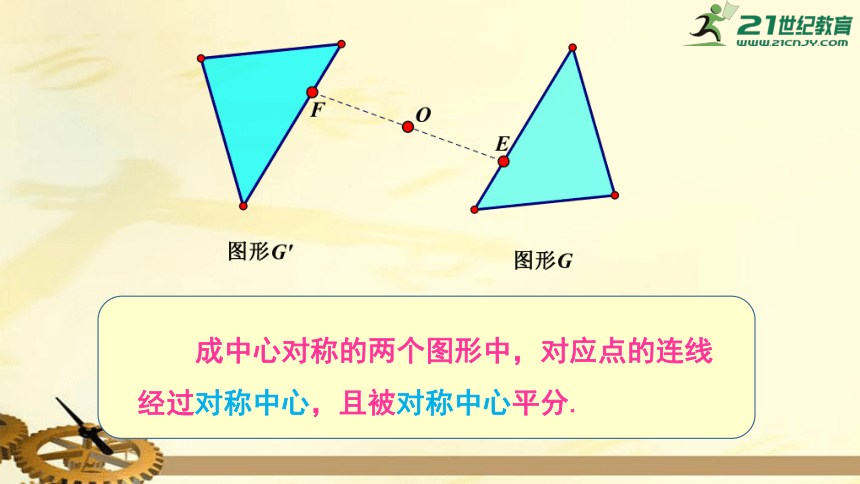
成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.
如图,已知△ABC
和点
O,
求作一个
△A′
B′
C′
,使它与
△ABC
关于点
O
成中心对称.
作法(1)
连接
AO
并延长
AO
到
A′,使
OA′
=
OA,于是得到点
A
关于点
O
的对应点A′.
(2)
用同样的方法作出点
B
和
C
关于点
O
的对应点
B′
和
C′.
(3)
连接
A′B′,
B′C′,
C′A′.
则△A′B′C′
即为所求作的三角形.
点击打开
【教材P51】
练习
【教材P52】
1.
判断(对的画“√”,
错的画“×”):
(1)线段
AB
的中点
O
是点
A
与点
B
的对称中心.
(
)
(2)等边三角形
ABC
的三条中线的交点是点
A
与
点
B
的对称中心.
(
)
√
×
2.画出
△ABC
关于点
A
成中心对称的图形.
【教材P52】
点击打开
作法(1)
延长
BA
到
B′,使
AB′
=
BA,于是得到点
B
关于点
A
的对应点
B′.
(2)
用同样的方法作出点
C
关于点
A
的对应点
C′.
(3)
连接
C′B′
则△AB′C′
即为所求作的三角形.
3.
如图,四边形
ABCD
与四边形
A′B′C′D′
关于某点
中心对称,找出它们的对称中心.
【教材P52】
随堂练习
1.
如图,
△ABC
和△DEF
关于点
O
成中心对称,要得到
△DEF,需要将△ABC
绕点
O
旋转(
)
A.30°
B.90°
C.180°
D.360
°
C
2.
如图,△ABC
与△DEF
关于点
O
成中心对称,
则线段
BC
与
EF
的关系是______________.
平行且相等
3.
如图,作出与△ABC
关于点
E
成中心对称的图形.
解:
依次寻找点
A
,
B
,
C
关于点
E
的对称点,
顺次连接,
所求作图形如图所示:
课堂小结
说一说什么是中心对称、对称中心和成中心对称?
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
中心对称概念及性质
第2章
四边形
湘教版·八年级下册
上课课件
学习目标
【知识与技能】
1.了解中心对称、对称中心和对称点的概念.
2.理解中心对称的性质.
3.掌握运用中心对称的性质作图的方法.
【过程与方法】
通过对中心对称的性质的探究及运用,初步学会从正反两方面去思考问题的数学思考方法,以及类比思想的应用.
【情感态度】
通过一系列探索活动,培养学生严谨的科学态度和探索的精神;经历数学知识融于生活实际的实习过程,体验数学学习的快乐.
【教学重点】
中心对称的概念;中心对称的性质;利用中心对称的性质进行作图.
【教学难点】
中心对称与轴对称的区别与联系,利用中心对称的性质准确作图.
新课导入
(1)把一个图案绕点
O
旋转
180°,你有什么发现?
点击打开
(2)如图,线段AC、BD
相交于点
O,OA
=
OC,OB
=
OD,把△OCD
绕点
O
旋转
180°,你有什么发现?
点击打开
在平面内,把一个图形上的每一个点
P
对应到它在绕点
O
旋转
180°下的像
P′,这个变换称为关于点
O
的中心对称.
在平面内,把点
E
绕点
O
旋转
180°得到点
F.
点击打开
此时称点
E
和点
F
关于点
O
对称,也称点
E
和点
F
是在这个旋转下的一对对应点.
由于点
E,O,F
在同一条直线上,且
OE
=
OF,因此点
O
是线段
EF
的中点.
反之,如果点
O
是线段
EF
的中点,那么点
E
和点
F
关于点
O
对称.
点击打开
在平面内,如果一个图形
G
绕点
O
旋转
180°,得到的像与另一个图形
G′
重合,
那么称这两个图形关于点
O
中心对称,点O
叫作对称中心.
成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.
如图,已知△ABC
和点
O,
求作一个
△A′
B′
C′
,使它与
△ABC
关于点
O
成中心对称.
作法(1)
连接
AO
并延长
AO
到
A′,使
OA′
=
OA,于是得到点
A
关于点
O
的对应点A′.
(2)
用同样的方法作出点
B
和
C
关于点
O
的对应点
B′
和
C′.
(3)
连接
A′B′,
B′C′,
C′A′.
则△A′B′C′
即为所求作的三角形.
点击打开
【教材P51】
练习
【教材P52】
1.
判断(对的画“√”,
错的画“×”):
(1)线段
AB
的中点
O
是点
A
与点
B
的对称中心.
(
)
(2)等边三角形
ABC
的三条中线的交点是点
A
与
点
B
的对称中心.
(
)
√
×
2.画出
△ABC
关于点
A
成中心对称的图形.
【教材P52】
点击打开
作法(1)
延长
BA
到
B′,使
AB′
=
BA,于是得到点
B
关于点
A
的对应点
B′.
(2)
用同样的方法作出点
C
关于点
A
的对应点
C′.
(3)
连接
C′B′
则△AB′C′
即为所求作的三角形.
3.
如图,四边形
ABCD
与四边形
A′B′C′D′
关于某点
中心对称,找出它们的对称中心.
【教材P52】
随堂练习
1.
如图,
△ABC
和△DEF
关于点
O
成中心对称,要得到
△DEF,需要将△ABC
绕点
O
旋转(
)
A.30°
B.90°
C.180°
D.360
°
C
2.
如图,△ABC
与△DEF
关于点
O
成中心对称,
则线段
BC
与
EF
的关系是______________.
平行且相等
3.
如图,作出与△ABC
关于点
E
成中心对称的图形.
解:
依次寻找点
A
,
B
,
C
关于点
E
的对称点,
顺次连接,
所求作图形如图所示:
课堂小结
说一说什么是中心对称、对称中心和成中心对称?
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
