2.3 中心对称和中心对称图形(第2课时) 中心对称图形 课件(共19张PPT)
文档属性
| 名称 | 2.3 中心对称和中心对称图形(第2课时) 中心对称图形 课件(共19张PPT) |  | |
| 格式 | rar | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 16:05:21 | ||
图片预览





文档简介
(共19张PPT)
中心对称图形
第2章
四边形
湘教版·八年级下册
上课课件
学习目标
【知识与技能】
使学生了解中心对称图形及其基本性质;掌握平行四边形是中心对称图形.
【过程与方法】
1.经历观察、发展、探索中心对称图形的有关概念和基本性质的过程,积累一定的审美体验.
2.了解中心对称图形及其基本性质,掌握平行四边形是中心对称图形.
【情感态度】
通过观察发现、动手操作、大胆猜想、自主探索、合作交流体验到成功的喜悦,学习的乐趣并积累一定的审美体验.
【教学重点】
中心对称图形的定义及其性质.
【教学难点】
中心对称图形与轴对称图形的区别;利用中心对称图形的有关概念和基本性质解决问题.
新课导入
1.
什么是轴对称?轴对称有哪些性质?
2.
对于轴对称图形,沿着某条对称轴对折能重合,那么有没有什么图形绕着某点旋转也能重合呢?
如图,将线段
AB
绕它的中点
O
旋转180°,
你有什么发现?
点击打开
像这样,如果一个图形绕一个点
O
旋转
180°,
所得到的像与原来的图形互相重合,那么这个图形叫作
中心对称图形,这个点
O
叫作它的对称中心.
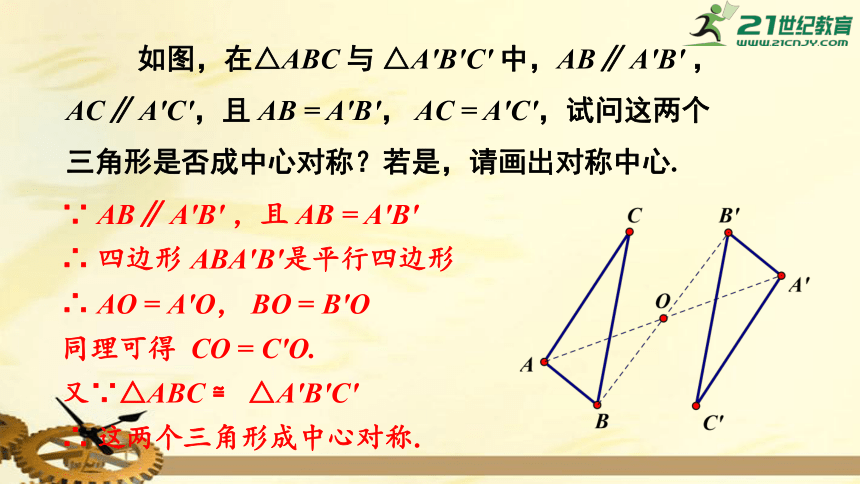
如图,在△ABC
与
△A′B′C′
中,AB∥
A′B′
,
AC∥
A′C′,且
AB
=
A′B′,
AC
=
A′C′,试问这两个三角形是否成中心对称?若是,请画出对称中心.
∵
AB∥
A′B′
,且
AB
=
A′B′
∴
四边形
ABA′B′是平行四边形
∴
AO
=
A′O,
BO
=
B′O
同理可得
CO
=
C′O.
又∵△ABC
≌
△A′B′C′
∴
这两个三角形成中心对称.
如图,□ABCD
的两条对角线相交于点
O,则
OA
=
OC,
OB
=
OD.
把
□ABCD
绕点
O
旋转180°,则:
(1)点
A
的像是
;
(2)点
B
的像是
;
(3)边
AB
的像是
;
(4)点
C
的像是
;
(5)边
BC
的像是
;
(6)点
D
的像
;
(7)边
CD
的像是
;
(8)边
DA
的像是
.
点击打开
点
C
点
D
边
CD
点
A
边
DA
点
B
边
AB
边
BC
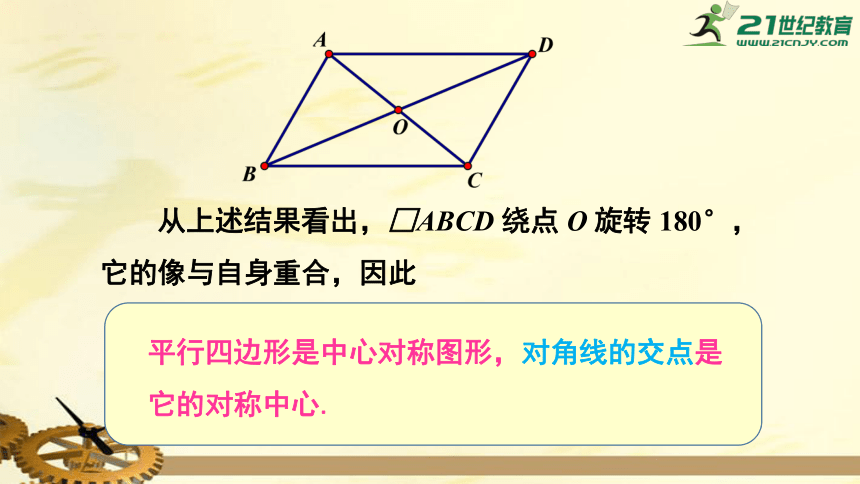
从上述结果看出,□ABCD
绕点
O
旋转
180°,它的像与自身重合,因此
平行四边形是中心对称图形,对角线的交点是它的对称中心.
你能利用平行四边形是中心对称图形,将其绕对称中心旋转
180°,来理解平行四边形的性质吗?
对边相等
对角相等
对角线互相平分
√
√
√
如图,O1、O2
分别是两个半圆的圆心,这个图形是中心对称图形吗?如果不是,请说明理由;如果是,请指出对称中心.
点击打开
练习
【教材P54】
1.
试举出生活中一些中心对称图形的例子.
2.
下列图形中,哪些是中心对称图形?如果是,找出它们的对称中心.
【教材P54】
答:图形(1)是中心对称图形,中心点
O
为其对称中心;
图形(2)是中心对称图形,圆心为其对称中心;
图形(3)不是中心对称图形.
随堂练习
1.
如图是正三角形、正六边形、正八边形,它们是中心
对称图形吗?
如果是,找出它们的对称中心.
【教材P54】
不是
是
是
2.
下列图形中,既是中心对称图形,又是轴对称
图形的有(
)
【教材P54】
A
3.如图,□
ABCD
的对角线
BD
=
4
cm,将
□ABCD
绕其对称中心旋转
180°,求点
D
所转过的路径长.
点击打开
点
D
所转过的路径是以
O
为圆心,BD
为直径的半圆.
l
=
πr
≈3.14×2
=
6.28
(cm)
什么是中心对称图形?
课堂小结
如果一个图形绕一个点
O
旋转
180°,
所得到的像与原来的图形互相重合,那么这个图形叫作中心对称图形,这个点
O
叫作它的对称中心.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
中心对称图形
第2章
四边形
湘教版·八年级下册
上课课件
学习目标
【知识与技能】
使学生了解中心对称图形及其基本性质;掌握平行四边形是中心对称图形.
【过程与方法】
1.经历观察、发展、探索中心对称图形的有关概念和基本性质的过程,积累一定的审美体验.
2.了解中心对称图形及其基本性质,掌握平行四边形是中心对称图形.
【情感态度】
通过观察发现、动手操作、大胆猜想、自主探索、合作交流体验到成功的喜悦,学习的乐趣并积累一定的审美体验.
【教学重点】
中心对称图形的定义及其性质.
【教学难点】
中心对称图形与轴对称图形的区别;利用中心对称图形的有关概念和基本性质解决问题.
新课导入
1.
什么是轴对称?轴对称有哪些性质?
2.
对于轴对称图形,沿着某条对称轴对折能重合,那么有没有什么图形绕着某点旋转也能重合呢?
如图,将线段
AB
绕它的中点
O
旋转180°,
你有什么发现?
点击打开
像这样,如果一个图形绕一个点
O
旋转
180°,
所得到的像与原来的图形互相重合,那么这个图形叫作
中心对称图形,这个点
O
叫作它的对称中心.
如图,在△ABC
与
△A′B′C′
中,AB∥
A′B′
,
AC∥
A′C′,且
AB
=
A′B′,
AC
=
A′C′,试问这两个三角形是否成中心对称?若是,请画出对称中心.
∵
AB∥
A′B′
,且
AB
=
A′B′
∴
四边形
ABA′B′是平行四边形
∴
AO
=
A′O,
BO
=
B′O
同理可得
CO
=
C′O.
又∵△ABC
≌
△A′B′C′
∴
这两个三角形成中心对称.
如图,□ABCD
的两条对角线相交于点
O,则
OA
=
OC,
OB
=
OD.
把
□ABCD
绕点
O
旋转180°,则:
(1)点
A
的像是
;
(2)点
B
的像是
;
(3)边
AB
的像是
;
(4)点
C
的像是
;
(5)边
BC
的像是
;
(6)点
D
的像
;
(7)边
CD
的像是
;
(8)边
DA
的像是
.
点击打开
点
C
点
D
边
CD
点
A
边
DA
点
B
边
AB
边
BC
从上述结果看出,□ABCD
绕点
O
旋转
180°,它的像与自身重合,因此
平行四边形是中心对称图形,对角线的交点是它的对称中心.
你能利用平行四边形是中心对称图形,将其绕对称中心旋转
180°,来理解平行四边形的性质吗?
对边相等
对角相等
对角线互相平分
√
√
√
如图,O1、O2
分别是两个半圆的圆心,这个图形是中心对称图形吗?如果不是,请说明理由;如果是,请指出对称中心.
点击打开
练习
【教材P54】
1.
试举出生活中一些中心对称图形的例子.
2.
下列图形中,哪些是中心对称图形?如果是,找出它们的对称中心.
【教材P54】
答:图形(1)是中心对称图形,中心点
O
为其对称中心;
图形(2)是中心对称图形,圆心为其对称中心;
图形(3)不是中心对称图形.
随堂练习
1.
如图是正三角形、正六边形、正八边形,它们是中心
对称图形吗?
如果是,找出它们的对称中心.
【教材P54】
不是
是
是
2.
下列图形中,既是中心对称图形,又是轴对称
图形的有(
)
【教材P54】
A
3.如图,□
ABCD
的对角线
BD
=
4
cm,将
□ABCD
绕其对称中心旋转
180°,求点
D
所转过的路径长.
点击打开
点
D
所转过的路径是以
O
为圆心,BD
为直径的半圆.
l
=
πr
≈3.14×2
=
6.28
(cm)
什么是中心对称图形?
课堂小结
如果一个图形绕一个点
O
旋转
180°,
所得到的像与原来的图形互相重合,那么这个图形叫作中心对称图形,这个点
O
叫作它的对称中心.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
