2.4 三角形的中位线 课件(共17张PPT)
文档属性
| 名称 | 2.4 三角形的中位线 课件(共17张PPT) |

|
|
| 格式 | rar | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
三角形的中位线
第2章
四边形
湘教版·八年级下册
上课课件
学习目标
【知识与技能】
1.进一步使学生掌握三角形相似的有关知识.
2.能够利用三角形的中位线的知识解决三角形相似的问题.
3.掌握三角形的中位线的性质和应用.
【过程与方法】
进一步使学生掌握三角形相似的有关知识;训练学生利用三角形的中位线的知识解决三角形相似的问题;把“三角形的中位线”这一知识提升为解决图形比例关系的一个“基本相似形”,形成三角形的中位线是相似问题的一种快速算法.
【情感态度】
经历从认识发现三角形的中位线到推理三角形的中位线的性质的过程,体会探索发现的乐趣,增强学习数学的自信心,使学生掌握三角形相似的有关知识.通过观察、讨论、比较,研究三角形的中位线的图象和性质,培养学生收集提取信息的意识和推理能力,使学生会将复杂问题转化为简单问题.培养学生的数形结合的思想.
【教学重点】
三角形中位线的性质和应用.
【教学难点】
正确的理解题意,发现“中点+中点是中位线”的条件,把复杂的图形转化为基本图形,培养学生数形结合的思想.
新课导入
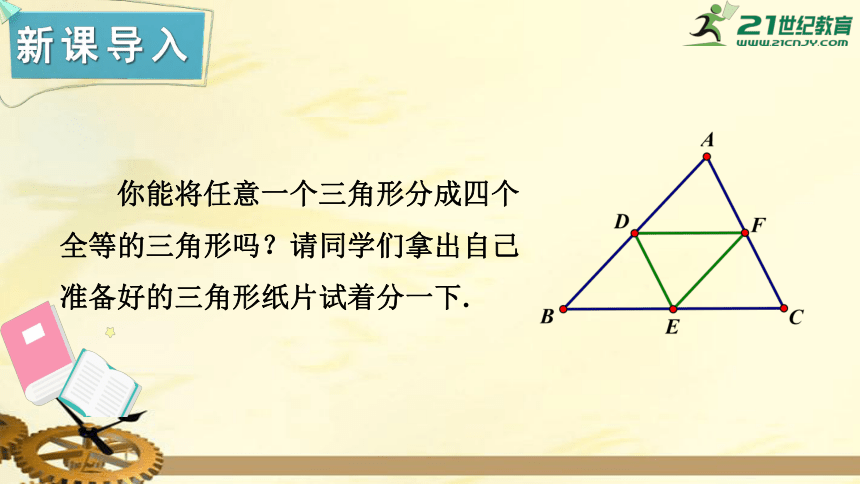
你能将任意一个三角形分成四个全等的三角形吗?请同学们拿出自己准备好的三角形纸片试着分一下.
连接三角形两边中点的线段叫做三角形的中位线.
如图,D,E,F
分别为△ABC
三边中点,所以,DF,DE,EF
分别是三角形的三条中位线.
注意区分中线和中位线.
如图,EF
是
△ABC
的一条中位线.
EF∥BC
吗?量一量
EF
与
BC
的长各是多少?
你能猜测出
EF
和
BC
具有怎样的位置关系和数量关
系吗?为什么?
猜测
如何证明?
点击打开
三角形的中位线定理:
三角形的中位线平行于第三边,并且等于第三边的一半.
EF∥BC,且
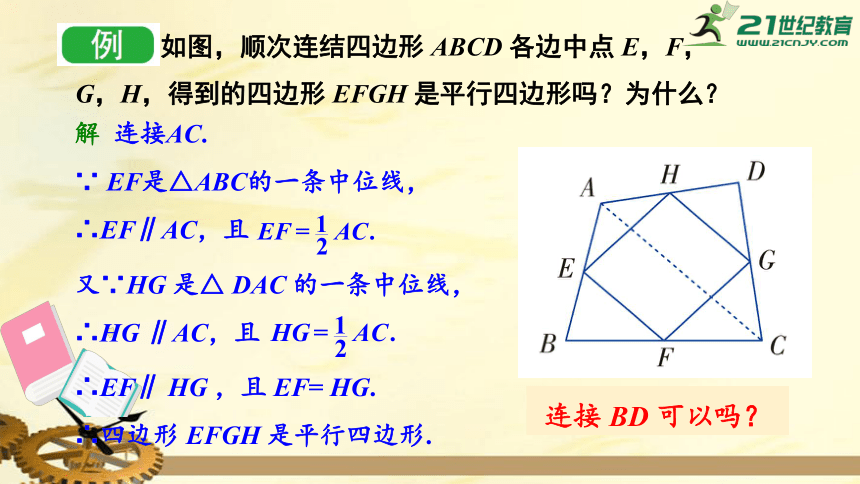
如图,顺次连结四边形
ABCD
各边中点
E,F,G,H,得到的四边形
EFGH
是平行四边形吗?为什么?
解
连接AC.
∵
EF是△ABC的一条中位线,
又∵HG
是△
DAC
的一条中位线,
∴EF∥
HG
,且
EF=
HG.
∴四边形
EFGH
是平行四边形.
∴EF∥AC,且
∴HG
∥AC,且
连接
BD
可以吗?
练习
【教材P56】
已知△ABC
的各边长度分别为
3
cm,
3.4
cm,
4
cm,求连接各边中点所构成的△DEF
的周长.
答:△DEF
的周长为
5.2
cm.
(1)四边形
ADEF
是平行四边形吗?为什么?
2.
如图,△ABC
的边
AB
,BC,CA
的中点分别是
D,E,F.
(2)四边形
ADEF
的周长等于
AB+AC
吗?为什么?
(1)四边形
ADEF
是平行四边形.
∵
∴四边形
ADEF
是平行四边形.
(1)四边形
ADEF
是平行四边形吗?为什么?
2.
如图,△ABC
的边
AB
,BC,CA
的中点分别是
D,E,F.
(2)四边形
ADEF
的周长等于
AB+AC
吗?为什么?
(2)是.
随堂练习
1.
如图,
在
Rt△ABC
中,∠A
=30°,
BC
=1,
点
D
,
E
分别是直角边
BC,
AC
的中点,
则
DE
的长为(
)
A.
1
B.
2
C.
D.
A
2.
(易错题)如图,在四边形
ABCD
中,
R
,
P
分别是
BC,
CD
上的点,
E
,
F
分别是
AP
,
RP
的中点,当点
P
在
CD
上从点
C
向点
D
移动而点
R
不动时,下列结论成立的是(
)
A.线段
EF
的长逐渐增大
B.线段
EF
的长逐渐减小
C.线段
EF
的长不变
D.线段
EF
的长与点
P
的位置有关
C
3.
如图,已知
D
,
E
,
F
分别是△ABC
各边的中点,
求证:
AE
与
DF
互相平分.
证明:∵
D,
E,
F
分别是△ABC
各边
的中点,根据中位线定理,可得
DE∥AC
,
EF∥AB,
∴四边形
ADEF
为平行四边形.
∴AE
与
DF
互相平分.
课堂小结
三角形的中位线定理:
三角形的中位线平行于第三边,并且等于第三边的一半.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
三角形的中位线
第2章
四边形
湘教版·八年级下册
上课课件
学习目标
【知识与技能】
1.进一步使学生掌握三角形相似的有关知识.
2.能够利用三角形的中位线的知识解决三角形相似的问题.
3.掌握三角形的中位线的性质和应用.
【过程与方法】
进一步使学生掌握三角形相似的有关知识;训练学生利用三角形的中位线的知识解决三角形相似的问题;把“三角形的中位线”这一知识提升为解决图形比例关系的一个“基本相似形”,形成三角形的中位线是相似问题的一种快速算法.
【情感态度】
经历从认识发现三角形的中位线到推理三角形的中位线的性质的过程,体会探索发现的乐趣,增强学习数学的自信心,使学生掌握三角形相似的有关知识.通过观察、讨论、比较,研究三角形的中位线的图象和性质,培养学生收集提取信息的意识和推理能力,使学生会将复杂问题转化为简单问题.培养学生的数形结合的思想.
【教学重点】
三角形中位线的性质和应用.
【教学难点】
正确的理解题意,发现“中点+中点是中位线”的条件,把复杂的图形转化为基本图形,培养学生数形结合的思想.
新课导入
你能将任意一个三角形分成四个全等的三角形吗?请同学们拿出自己准备好的三角形纸片试着分一下.
连接三角形两边中点的线段叫做三角形的中位线.
如图,D,E,F
分别为△ABC
三边中点,所以,DF,DE,EF
分别是三角形的三条中位线.
注意区分中线和中位线.
如图,EF
是
△ABC
的一条中位线.
EF∥BC
吗?量一量
EF
与
BC
的长各是多少?
你能猜测出
EF
和
BC
具有怎样的位置关系和数量关
系吗?为什么?
猜测
如何证明?
点击打开
三角形的中位线定理:
三角形的中位线平行于第三边,并且等于第三边的一半.
EF∥BC,且
如图,顺次连结四边形
ABCD
各边中点
E,F,G,H,得到的四边形
EFGH
是平行四边形吗?为什么?
解
连接AC.
∵
EF是△ABC的一条中位线,
又∵HG
是△
DAC
的一条中位线,
∴EF∥
HG
,且
EF=
HG.
∴四边形
EFGH
是平行四边形.
∴EF∥AC,且
∴HG
∥AC,且
连接
BD
可以吗?
练习
【教材P56】
已知△ABC
的各边长度分别为
3
cm,
3.4
cm,
4
cm,求连接各边中点所构成的△DEF
的周长.
答:△DEF
的周长为
5.2
cm.
(1)四边形
ADEF
是平行四边形吗?为什么?
2.
如图,△ABC
的边
AB
,BC,CA
的中点分别是
D,E,F.
(2)四边形
ADEF
的周长等于
AB+AC
吗?为什么?
(1)四边形
ADEF
是平行四边形.
∵
∴四边形
ADEF
是平行四边形.
(1)四边形
ADEF
是平行四边形吗?为什么?
2.
如图,△ABC
的边
AB
,BC,CA
的中点分别是
D,E,F.
(2)四边形
ADEF
的周长等于
AB+AC
吗?为什么?
(2)是.
随堂练习
1.
如图,
在
Rt△ABC
中,∠A
=30°,
BC
=1,
点
D
,
E
分别是直角边
BC,
AC
的中点,
则
DE
的长为(
)
A.
1
B.
2
C.
D.
A
2.
(易错题)如图,在四边形
ABCD
中,
R
,
P
分别是
BC,
CD
上的点,
E
,
F
分别是
AP
,
RP
的中点,当点
P
在
CD
上从点
C
向点
D
移动而点
R
不动时,下列结论成立的是(
)
A.线段
EF
的长逐渐增大
B.线段
EF
的长逐渐减小
C.线段
EF
的长不变
D.线段
EF
的长与点
P
的位置有关
C
3.
如图,已知
D
,
E
,
F
分别是△ABC
各边的中点,
求证:
AE
与
DF
互相平分.
证明:∵
D,
E,
F
分别是△ABC
各边
的中点,根据中位线定理,可得
DE∥AC
,
EF∥AB,
∴四边形
ADEF
为平行四边形.
∴AE
与
DF
互相平分.
课堂小结
三角形的中位线定理:
三角形的中位线平行于第三边,并且等于第三边的一半.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
