2.1.4 多项式的乘法(第2课时) 多项式与多项式相乘 课件(共22张PPT)
文档属性
| 名称 | 2.1.4 多项式的乘法(第2课时) 多项式与多项式相乘 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 17:12:20 | ||
图片预览




文档简介
(共22张PPT)
多项式与多项式相乘
第2章
整式的乘法
湘教版·七年级数学下册
上课课件
学习目标
【知识与技能】
在具体情境中了解多项式乘法的意义,会利用法则进行简单的多项式乘法运算.
【过程与方法】
经历探索多项式与多项式乘法法则的过程,理解多项式与多项式相乘的运算算理,体会乘法分配律的作用及转化思想在解决问题过程中的应用,发展学生有条理的思考和语言表达能力.
【情感态度】
在解决问题的过程中了解数学的价值,发展“用数学”的信心.
【教学重点】
熟悉多项式与多项式乘法法则.
【教学难点】
理解多项式与多项式相乘的算理.
复习导入
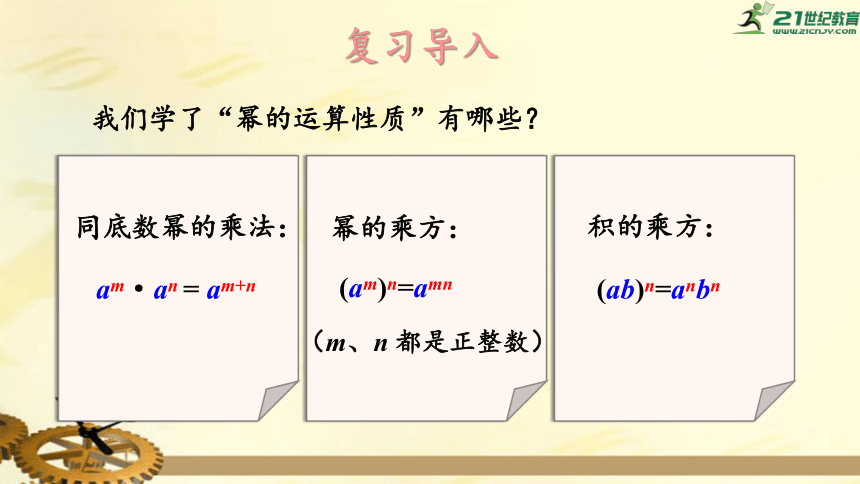
我们学了“幂的运算性质”有哪些?
同底数幂的乘法:
am·an
=
am+n
幂的乘方:
(am)n=amn
(m、n
都是正整数)
积的乘方:
(ab)n=anbn
单项式乘以多项式的法则是什么?
m
(a
+
b
+
c)
=
ma
+
mb
+
mc
复习导入
一般地,单项式与多项式相乘,先用单项式乘多项式中的每一项,再把所得的积相加.
探究新知
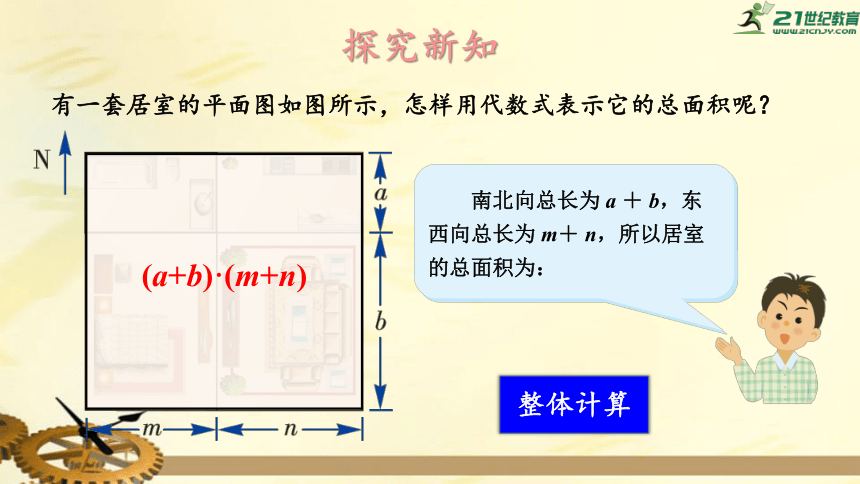
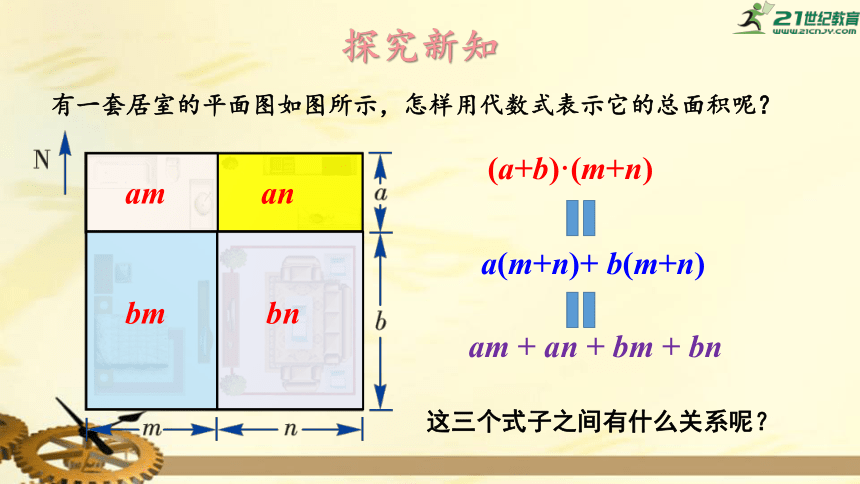
有一套居室的平面图如图所示,怎样用代数式表示它的总面积呢?
南北向总长为
a
+
b,东西向总长为
m+
n,所以居室的总面积为:
(a+b)·(m+n)
整体计算
探究新知
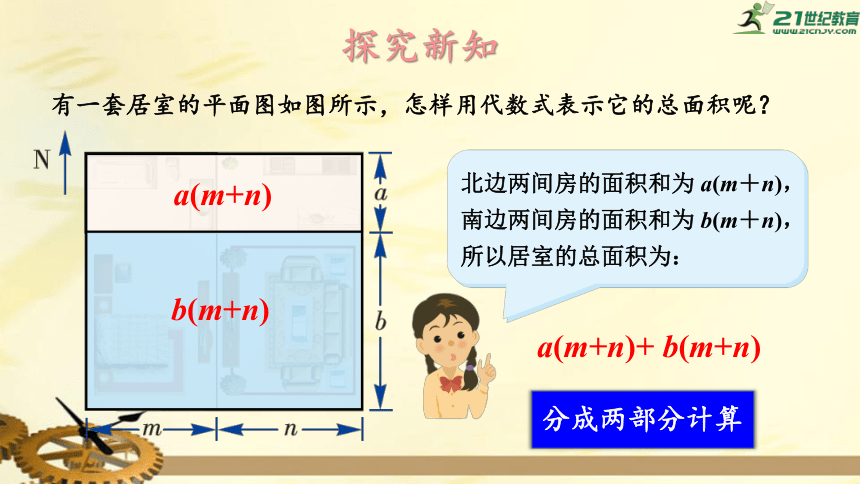
有一套居室的平面图如图所示,怎样用代数式表示它的总面积呢?
a(m+n)
a(m+n)+
b(m+n)
北边两间房的面积和为
a(m+n),南边两间房的面积和为
b(m+n),
所以居室的总面积为:
b(m+n)
分成两部分计算
探究新知
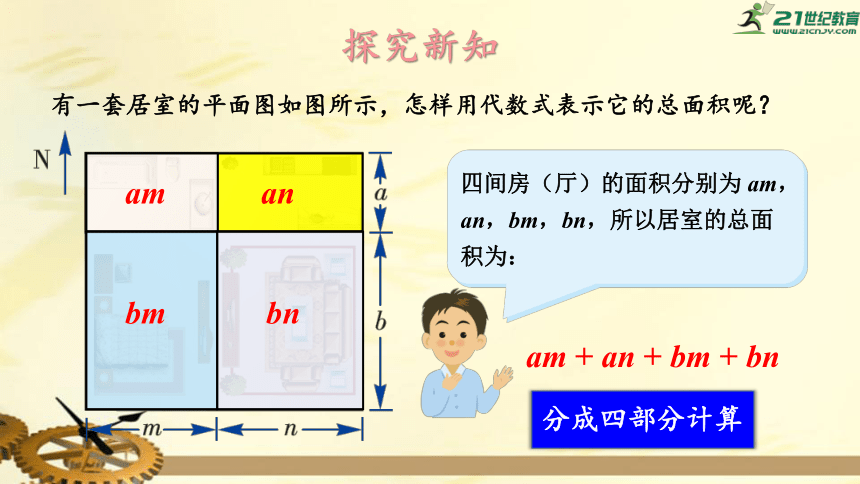
有一套居室的平面图如图所示,怎样用代数式表示它的总面积呢?
四间房(厅)的面积分别为
am,
an,bm,bn,所以居室的总面积为:
am
am
+
an
+
bm
+
bn
an
bm
bn
分成四部分计算
探究新知
有一套居室的平面图如图所示,怎样用代数式表示它的总面积呢?
am
am
+
an
+
bm
+
bn
an
bm
bn
(a+b)·(m+n)
a(m+n)+
b(m+n)
这三个式子之间有什么关系呢?
am
+
an
+
bm
+
bn
(a+b)·(m+n)
a(m+n)+
b(m+n)
=
=
你能说出这一步运算的道理吗?
(a+b)·(m+n)
a(m+n)+
b(m+n)
=
这一步是把
m
+
n
看成一个整体,利用乘法分配律得到
a
(
m
+
n
)
+
b
(
m
+
n
)
.
am
+
an
+
bm
+
bn
a(m+n)+
b(m+n)
(a+b)·(m+n)
=
=
(a+b)·(m+n)
=
am
+
an
+
bm
+
bn
你能说说如何进行多项式与多项式相乘的运算?
am
+
an
+
bm
+
bn
a(m+n)+
b(m+n)
(a+b)·(m+n)
=
=
(a+b)·(m+n)
=
am
+
an
+
bm
+
bn
Ⅰ
Ⅰ
Ⅱ
Ⅱ
Ⅲ
Ⅲ
Ⅳ
Ⅳ
一般地,多项式与多项式相乘,先用一个多项式的每一项分别乘另一个多项式的每一项,再把所得的积相加.
计算:(1)(
2x
+
y
)(
x
–
3y
);
(2)(
2x
+
1
)(
3x2
–
x
–
5
);
(3)(
x
+
a
)(
x
+
b
).
解
(1)(
2x
+
y
)(
x
-3y
)
=
2x
·
x
+
2x
·(-3y)+
y
·
x
+
y
·(-3y)
=
2x2-6xy
+
yx
-3y2
=
2x2-
5xy
-3y2
计算:(1)(
2x
+
y
)(
x
–
3y
);
(2)(
2x
+
1
)(
3x2
–
x
–
5
);
(3)(
x
+
a
)(
x
+
b
).
(2)(
2x
+
1
)(
3x2
-
x
–
5
)
=
6x3
-
2x2
–
10x
+
3x2
–
x
-
5
=
6x3
+
x2
-
11x
-
5.
计算:(1)(
2x
+
y
)(
x
–
3y
);
(2)(
2x
+
1
)(
3x2
–
x
–
5
);
(3)(
x
+
a
)(
x
+
b
).
(3)
(
x
+
a
)(
x
+
b
)
=
x2
+
bx
+
ax
+
ab
=
x2
+
(
a
+
b
)x
+
ab
第(3)小题的直观意义如图
解(1)(a+b)(a-b)
=
a2-ab+ba-b2
=
a2-b2
=
(a+b)(a+b)
=
a2+ab+ba+b2
(2)(a+b)2
=
a2+2ab+b2
(1)(a+b)(a-b);
(2)(a+b)2
;
(3)(a-b)2.
(3)(a-b)2
=
(a-b)(a-b)
=
a2-ab-ba+b2
=
a2-2ab+b2
巩固练习
1.
下列计算对不对?
如果不对,
应怎样改正?
(1)(
3a-b
)(
2a
+
b
)
=
3a·2a
+
(
-
b
)·b
=
6a2-
b2;
(2)
(
x
+
3
)
(
1
-
x
)
=
x·1
+
x·x
+
3
-
3·x
=
x2
-
2x
+
3
.
解:(1)不对,应为
(
3a-b
)(
2a
+
b
)
=
3a·2a
+
3a·b
-
b
·2a
-
b
·b
=
6a2
+
ab
-
b2
;
(2)不对,应为
(
x
+
3
)
(
1
-
x
)=
x·1-
x·x
+
3×1-3·x
=
x
-
x2
+
3-3x
=
-x2-2x
+
3
2.
计算:
(1)(
x-2
)(
x
+
3
)
;(2)
(
x
+
1
)
(
x
+
5
)
;
(3)(
x
+
4
)(
x
-
5
);(4)(
x
-
3
)2.
解:(1)(
x-2
)(
x
+
3
)
=
x2
+3x-2x-6
=
x2
+
x-6;
(2)
(
x
+
1
)
(
x
+
5
)
=
x2
+
6x
+
5;
(3)(
x
+
4
)(
x
-
5
)=
x2-5x
+
4x-20
=
x2-x-20
(4)(
x
-
3
)2
=
(
x
-
3
)
(
x
-
3
)
=
x2-3x+9
=
x2-6x+9
3.
计算:
(1)(
x
+
2y
)2
;
(2)
(
m
–
2n
)
(
2m
+
n
)
;
(3)(
3a
+
2b
)(
3a
–
2b
);
(4)(
3a
–
2b
)2.
解:(1)(x+2y)2=
(x+2y)
(x+2y)=x2+2xy+2xy+4y2=x2+4xy+4y2;
(2)
(m–2n)
(2m+n)=2m2+mn-4mn-2n2=2m2-3mn-2n2
(3)(
3a
+
2b
)(
3a
–
2b
)=9a2-4b2
(4)(
3a
–
2b
)2
=
(3a–2b)
(3a–2b
)
=
9a2-6ab-6ab+4b2
=
9a2-12ab+4b2
课堂小结
一般地,多项式与多项式相乘,先用一个多项式的每一项分别乘另一个多项式的每一项,再把所得的积相加.
(a+b)·(m+n)
=
am
+
an
+
bm
+
bn
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
多项式与多项式相乘
第2章
整式的乘法
湘教版·七年级数学下册
上课课件
学习目标
【知识与技能】
在具体情境中了解多项式乘法的意义,会利用法则进行简单的多项式乘法运算.
【过程与方法】
经历探索多项式与多项式乘法法则的过程,理解多项式与多项式相乘的运算算理,体会乘法分配律的作用及转化思想在解决问题过程中的应用,发展学生有条理的思考和语言表达能力.
【情感态度】
在解决问题的过程中了解数学的价值,发展“用数学”的信心.
【教学重点】
熟悉多项式与多项式乘法法则.
【教学难点】
理解多项式与多项式相乘的算理.
复习导入
我们学了“幂的运算性质”有哪些?
同底数幂的乘法:
am·an
=
am+n
幂的乘方:
(am)n=amn
(m、n
都是正整数)
积的乘方:
(ab)n=anbn
单项式乘以多项式的法则是什么?
m
(a
+
b
+
c)
=
ma
+
mb
+
mc
复习导入
一般地,单项式与多项式相乘,先用单项式乘多项式中的每一项,再把所得的积相加.
探究新知
有一套居室的平面图如图所示,怎样用代数式表示它的总面积呢?
南北向总长为
a
+
b,东西向总长为
m+
n,所以居室的总面积为:
(a+b)·(m+n)
整体计算
探究新知
有一套居室的平面图如图所示,怎样用代数式表示它的总面积呢?
a(m+n)
a(m+n)+
b(m+n)
北边两间房的面积和为
a(m+n),南边两间房的面积和为
b(m+n),
所以居室的总面积为:
b(m+n)
分成两部分计算
探究新知
有一套居室的平面图如图所示,怎样用代数式表示它的总面积呢?
四间房(厅)的面积分别为
am,
an,bm,bn,所以居室的总面积为:
am
am
+
an
+
bm
+
bn
an
bm
bn
分成四部分计算
探究新知
有一套居室的平面图如图所示,怎样用代数式表示它的总面积呢?
am
am
+
an
+
bm
+
bn
an
bm
bn
(a+b)·(m+n)
a(m+n)+
b(m+n)
这三个式子之间有什么关系呢?
am
+
an
+
bm
+
bn
(a+b)·(m+n)
a(m+n)+
b(m+n)
=
=
你能说出这一步运算的道理吗?
(a+b)·(m+n)
a(m+n)+
b(m+n)
=
这一步是把
m
+
n
看成一个整体,利用乘法分配律得到
a
(
m
+
n
)
+
b
(
m
+
n
)
.
am
+
an
+
bm
+
bn
a(m+n)+
b(m+n)
(a+b)·(m+n)
=
=
(a+b)·(m+n)
=
am
+
an
+
bm
+
bn
你能说说如何进行多项式与多项式相乘的运算?
am
+
an
+
bm
+
bn
a(m+n)+
b(m+n)
(a+b)·(m+n)
=
=
(a+b)·(m+n)
=
am
+
an
+
bm
+
bn
Ⅰ
Ⅰ
Ⅱ
Ⅱ
Ⅲ
Ⅲ
Ⅳ
Ⅳ
一般地,多项式与多项式相乘,先用一个多项式的每一项分别乘另一个多项式的每一项,再把所得的积相加.
计算:(1)(
2x
+
y
)(
x
–
3y
);
(2)(
2x
+
1
)(
3x2
–
x
–
5
);
(3)(
x
+
a
)(
x
+
b
).
解
(1)(
2x
+
y
)(
x
-3y
)
=
2x
·
x
+
2x
·(-3y)+
y
·
x
+
y
·(-3y)
=
2x2-6xy
+
yx
-3y2
=
2x2-
5xy
-3y2
计算:(1)(
2x
+
y
)(
x
–
3y
);
(2)(
2x
+
1
)(
3x2
–
x
–
5
);
(3)(
x
+
a
)(
x
+
b
).
(2)(
2x
+
1
)(
3x2
-
x
–
5
)
=
6x3
-
2x2
–
10x
+
3x2
–
x
-
5
=
6x3
+
x2
-
11x
-
5.
计算:(1)(
2x
+
y
)(
x
–
3y
);
(2)(
2x
+
1
)(
3x2
–
x
–
5
);
(3)(
x
+
a
)(
x
+
b
).
(3)
(
x
+
a
)(
x
+
b
)
=
x2
+
bx
+
ax
+
ab
=
x2
+
(
a
+
b
)x
+
ab
第(3)小题的直观意义如图
解(1)(a+b)(a-b)
=
a2-ab+ba-b2
=
a2-b2
=
(a+b)(a+b)
=
a2+ab+ba+b2
(2)(a+b)2
=
a2+2ab+b2
(1)(a+b)(a-b);
(2)(a+b)2
;
(3)(a-b)2.
(3)(a-b)2
=
(a-b)(a-b)
=
a2-ab-ba+b2
=
a2-2ab+b2
巩固练习
1.
下列计算对不对?
如果不对,
应怎样改正?
(1)(
3a-b
)(
2a
+
b
)
=
3a·2a
+
(
-
b
)·b
=
6a2-
b2;
(2)
(
x
+
3
)
(
1
-
x
)
=
x·1
+
x·x
+
3
-
3·x
=
x2
-
2x
+
3
.
解:(1)不对,应为
(
3a-b
)(
2a
+
b
)
=
3a·2a
+
3a·b
-
b
·2a
-
b
·b
=
6a2
+
ab
-
b2
;
(2)不对,应为
(
x
+
3
)
(
1
-
x
)=
x·1-
x·x
+
3×1-3·x
=
x
-
x2
+
3-3x
=
-x2-2x
+
3
2.
计算:
(1)(
x-2
)(
x
+
3
)
;(2)
(
x
+
1
)
(
x
+
5
)
;
(3)(
x
+
4
)(
x
-
5
);(4)(
x
-
3
)2.
解:(1)(
x-2
)(
x
+
3
)
=
x2
+3x-2x-6
=
x2
+
x-6;
(2)
(
x
+
1
)
(
x
+
5
)
=
x2
+
6x
+
5;
(3)(
x
+
4
)(
x
-
5
)=
x2-5x
+
4x-20
=
x2-x-20
(4)(
x
-
3
)2
=
(
x
-
3
)
(
x
-
3
)
=
x2-3x+9
=
x2-6x+9
3.
计算:
(1)(
x
+
2y
)2
;
(2)
(
m
–
2n
)
(
2m
+
n
)
;
(3)(
3a
+
2b
)(
3a
–
2b
);
(4)(
3a
–
2b
)2.
解:(1)(x+2y)2=
(x+2y)
(x+2y)=x2+2xy+2xy+4y2=x2+4xy+4y2;
(2)
(m–2n)
(2m+n)=2m2+mn-4mn-2n2=2m2-3mn-2n2
(3)(
3a
+
2b
)(
3a
–
2b
)=9a2-4b2
(4)(
3a
–
2b
)2
=
(3a–2b)
(3a–2b
)
=
9a2-6ab-6ab+4b2
=
9a2-12ab+4b2
课堂小结
一般地,多项式与多项式相乘,先用一个多项式的每一项分别乘另一个多项式的每一项,再把所得的积相加.
(a+b)·(m+n)
=
am
+
an
+
bm
+
bn
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
