2.2.1 平方差公式 课件(共21张PPT)
文档属性
| 名称 | 2.2.1 平方差公式 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
平方差公式
第2章
整式的乘法
湘教版·七年级数学下册
上课课件
学习目标
【知识与技能】
1.使学生理解和掌握平方差公式.
2.会利用公式进行计算,能够掌握平方差公式的一些应用.
【过程与方法】
经历探索平方差公式的过程,增强了数和符号的意识,培养学生发现问题、提出问题的能力.
【情感态度】
在探索和交流的过程中,培养学生与人协作的习惯,质疑的精神.
【教学重点】
弄清平方差公式的来源及其结构特点,能用自己的语言说明公式及其特点.
【教学难点】
准确理解和掌握公式的结构特征.
复习导入
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
符号表示:(m+b)(n+a)
=
mn
+
ma
+
bn
+
ba.
两项式乘以两项式,结果可能是两项吗?请你举例说明.
探究新知
计算下列各式,你能发现什么规律:
(a
+
2
)(
a
–
2)
=
a2
-
2a
+
2a
-
22=
,
(a
+
1
)(
a
-
1)
=
a2
-
a
+
a
-
12=
,
(a
+
3
)(
a
-
3)
=
a2
-
3a
+
3a
-32=
,
(a
+
4
)(
a
-
4
)
=
a2
-
4a
+
4a
-42=
.
a2-
12
a2-
22
a2-
32
a2-42
(a
+
b
)(
a
-
b
)
=
a2
-
ab
+
ab
-b2=
.
a2-b2
(a
+
b
)(
a
-
b
)
=
a2
-
ab
+
ab
-b2=
.
a2-b2
(a
+
b
)(
a
-
b
)
=
a2-b2
平方差公式
两个数的和与这两个数的差的积等于这两个数的平方差.
(a
+
b
)(
a
-
b
)
=
a2-b2
应用平方差公式时应注意些什么呢?
(1)注意平方差公式的适用范围;
(2)字母
a、b
可以是数,也可以是整式;
(3)注意计算过程中的符号和括号.
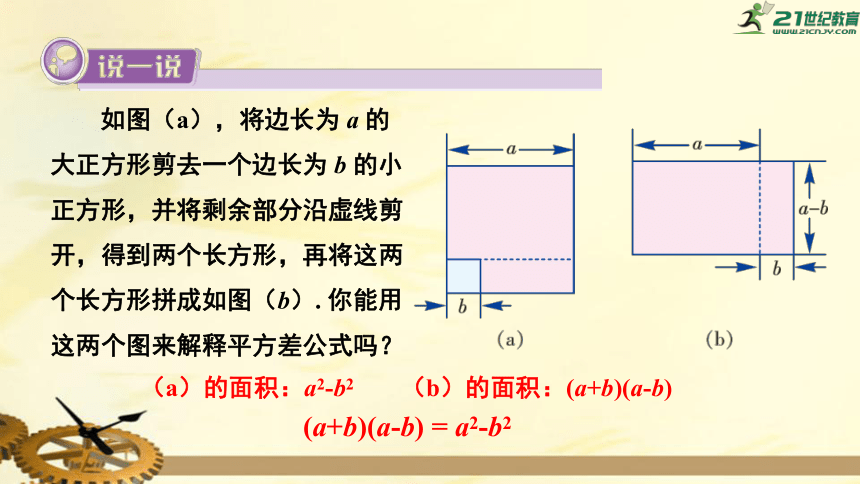
如图(a),将边长为
a
的大正方形剪去一个边长为
b
的小正方形,并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成如图(b).
你能用这两个图来解释平方差公式吗?
(a)的面积:a2-b2
(b)的面积:(a+b)(a-b)
(a+b)(a-b)
=
a2-b2
(1)(2x+1)(2x-1);
(2)(x+2y)(x-2y).
运用平方差公式计算:
分析
第(1)题,可以把“2x”看成平方差公式中的“a”,
“1”看成“b”;第(2)题,可以把“x”看成平方差公式中的“a”,“2y”看成“b”.
解(1)(2x+1)(2x-1)
=
(2x)2-12
=
4x2-1.
(2)
(x+2y)(x-2y)
=
x2
-(2y)2
=
x2
-4y2
(2)(4a+b)(-b+4a).
(4a+b)(-b+4a)
=
(4a)2
-b2
=
16a2
-b2
运用平方差公式计算:
计算:1
002×998
解:
1
002×998
=
(1
000+2)(1
000-2)
=
1
0002-22
=
1
000
000-4
=
999
996
巩固练习
1.
下面各式的计算对不对?
如果不对,
应怎样改正?
(1)
(
x-
2
)(
x
+
2
)
=
x2-
2
;
(2)
(-2x-
1)(2x
-
1)
=
4x2-
1
.
解:(1)
(
x-
2
)(
x
+
2
)
=
x2-
4
;
(2)
(-2x-
1)(2x
-
1)
=
(-1-2x)(-1+2x)=
1-4x2
.
2.
运用平方差公式计算:
(2)(3a+b)(3a-b);
(1)(m+2n)(m-2n);
(4)(-1+5a)(-1-5a).
(3)
=
9a2-b2
=
m2-4n2
=
1-25a2.
=
x2-y2
(1)202×198;
(2)49.8×50.2
.
3.
计算:
解:(1)202×198
=
(200+2)(200-2)
=
40
000
–
4
=
39
996
(2)49.8×50.2
=
(50-0.2)(50+0.5)
=
2
500-0.04
=
2
499.96
随堂练习
(x+6)(x-6)
=_________.
1.
填空题:
(-x+
)(-x-
)
=_________.
(-2a2
-
5b
)(
)
=
4a2-25b2.
x2
-36
-2a2
+
5b
2.
下列式中能用平方差公式计算的有(
)
①
②
(3a-bc)(-bc-3a)
③
(3-x+y)(3+x+y)
④
(100+1)(100-1)
A.
1个
B.
2个
C.
3个
D.
4个
(x-
y)(x+
y)
D
3.
计算:
(1)
(2a-3b)(2a+3b);
(2)
(-p2+q)(-p2-q);
解:原式
=
(2a)2-(3b)2
=
4a2-9b2
原式
=
(-p2)2-(q)2
=
p4-q2
4.
计算
(a+1)(a-1)(a2+1)(a4+1)(a8+1).
解:原式
=
(a2-1)(a2+1)(a4+1)(a8+1)
=
(a4-1)(a4+1)(a8+1)
=
(a8-1)(a8+1)
=
a16-1
课堂小结
(a
+
b
)(
a
-
b
)
=
a2-b2
平方差公式
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
平方差公式
第2章
整式的乘法
湘教版·七年级数学下册
上课课件
学习目标
【知识与技能】
1.使学生理解和掌握平方差公式.
2.会利用公式进行计算,能够掌握平方差公式的一些应用.
【过程与方法】
经历探索平方差公式的过程,增强了数和符号的意识,培养学生发现问题、提出问题的能力.
【情感态度】
在探索和交流的过程中,培养学生与人协作的习惯,质疑的精神.
【教学重点】
弄清平方差公式的来源及其结构特点,能用自己的语言说明公式及其特点.
【教学难点】
准确理解和掌握公式的结构特征.
复习导入
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
符号表示:(m+b)(n+a)
=
mn
+
ma
+
bn
+
ba.
两项式乘以两项式,结果可能是两项吗?请你举例说明.
探究新知
计算下列各式,你能发现什么规律:
(a
+
2
)(
a
–
2)
=
a2
-
2a
+
2a
-
22=
,
(a
+
1
)(
a
-
1)
=
a2
-
a
+
a
-
12=
,
(a
+
3
)(
a
-
3)
=
a2
-
3a
+
3a
-32=
,
(a
+
4
)(
a
-
4
)
=
a2
-
4a
+
4a
-42=
.
a2-
12
a2-
22
a2-
32
a2-42
(a
+
b
)(
a
-
b
)
=
a2
-
ab
+
ab
-b2=
.
a2-b2
(a
+
b
)(
a
-
b
)
=
a2
-
ab
+
ab
-b2=
.
a2-b2
(a
+
b
)(
a
-
b
)
=
a2-b2
平方差公式
两个数的和与这两个数的差的积等于这两个数的平方差.
(a
+
b
)(
a
-
b
)
=
a2-b2
应用平方差公式时应注意些什么呢?
(1)注意平方差公式的适用范围;
(2)字母
a、b
可以是数,也可以是整式;
(3)注意计算过程中的符号和括号.
如图(a),将边长为
a
的大正方形剪去一个边长为
b
的小正方形,并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成如图(b).
你能用这两个图来解释平方差公式吗?
(a)的面积:a2-b2
(b)的面积:(a+b)(a-b)
(a+b)(a-b)
=
a2-b2
(1)(2x+1)(2x-1);
(2)(x+2y)(x-2y).
运用平方差公式计算:
分析
第(1)题,可以把“2x”看成平方差公式中的“a”,
“1”看成“b”;第(2)题,可以把“x”看成平方差公式中的“a”,“2y”看成“b”.
解(1)(2x+1)(2x-1)
=
(2x)2-12
=
4x2-1.
(2)
(x+2y)(x-2y)
=
x2
-(2y)2
=
x2
-4y2
(2)(4a+b)(-b+4a).
(4a+b)(-b+4a)
=
(4a)2
-b2
=
16a2
-b2
运用平方差公式计算:
计算:1
002×998
解:
1
002×998
=
(1
000+2)(1
000-2)
=
1
0002-22
=
1
000
000-4
=
999
996
巩固练习
1.
下面各式的计算对不对?
如果不对,
应怎样改正?
(1)
(
x-
2
)(
x
+
2
)
=
x2-
2
;
(2)
(-2x-
1)(2x
-
1)
=
4x2-
1
.
解:(1)
(
x-
2
)(
x
+
2
)
=
x2-
4
;
(2)
(-2x-
1)(2x
-
1)
=
(-1-2x)(-1+2x)=
1-4x2
.
2.
运用平方差公式计算:
(2)(3a+b)(3a-b);
(1)(m+2n)(m-2n);
(4)(-1+5a)(-1-5a).
(3)
=
9a2-b2
=
m2-4n2
=
1-25a2.
=
x2-y2
(1)202×198;
(2)49.8×50.2
.
3.
计算:
解:(1)202×198
=
(200+2)(200-2)
=
40
000
–
4
=
39
996
(2)49.8×50.2
=
(50-0.2)(50+0.5)
=
2
500-0.04
=
2
499.96
随堂练习
(x+6)(x-6)
=_________.
1.
填空题:
(-x+
)(-x-
)
=_________.
(-2a2
-
5b
)(
)
=
4a2-25b2.
x2
-36
-2a2
+
5b
2.
下列式中能用平方差公式计算的有(
)
①
②
(3a-bc)(-bc-3a)
③
(3-x+y)(3+x+y)
④
(100+1)(100-1)
A.
1个
B.
2个
C.
3个
D.
4个
(x-
y)(x+
y)
D
3.
计算:
(1)
(2a-3b)(2a+3b);
(2)
(-p2+q)(-p2-q);
解:原式
=
(2a)2-(3b)2
=
4a2-9b2
原式
=
(-p2)2-(q)2
=
p4-q2
4.
计算
(a+1)(a-1)(a2+1)(a4+1)(a8+1).
解:原式
=
(a2-1)(a2+1)(a4+1)(a8+1)
=
(a4-1)(a4+1)(a8+1)
=
(a8-1)(a8+1)
=
a16-1
课堂小结
(a
+
b
)(
a
-
b
)
=
a2-b2
平方差公式
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
