2.2.2 完全平方公式(第1课时) 完全平方公式 课件(共19张PPT)
文档属性
| 名称 | 2.2.2 完全平方公式(第1课时) 完全平方公式 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
完全平方公式
第2章
整式的乘法
湘教版·七年级数学下册
上课课件
学习目标
【知识与技能】
理解公式的本质,从不同的层次上理解完全平方公式,并会运用公式进行简单的计算,了解完全平方公式的几何背景.
【过程与方法】
经历探索完全平方公式的过程,并从推导过程中,培养学生观察、发现、归纳、概括、猜想等探究创新能力,发展逻辑推理能力和有条理的表达能力,培养学生的数形结合意识.
【情感态度】
在学习中使学生体会学习数学的乐趣,培养学习数学的信心,感受数学的内在美.
【教学重点】
1.
弄清完全平方公式的来源及其结构特点,用自己的语言说明公式及其特点。
2.会用完全平方公式进行运算.
【教学难点】
会用完全平方公式进行运算.
复习导入
同学们,前面我们学习了多项式乘多项式法则和合并同类项法则,你会计算下列各题吗?
(x+3)2
=
______________________,
(x-3)2
=
_______________________,
(x+3)
(x+3)
=
x2+6x+9
(x-3)
(x-3)
=
x2-6x+9
这些式子的左边和右边有什么规律?
(2m+3n)2=________________________________,
(2m-3n)2=______________________________.
(2m+3n)
(2m+3n)=4m2+12mn+9n2
(2m-3n)
(2m-3n)=4m2-12mn+9n2
探究新知
计算下列各式,你能发现什么规律?
(a+1)2
=
(a+1)
(a+1)
=
a2+
a
+
a
+
12
=
a2+
2a
+
12,
(a+2)2
=
__________=
______________
=
__________,
(a+3)2
=
__________=
______________
=
__________,
(a+4)2
=
__________=
______________=
__________.
(a+2)
(a+2)
a2+
4a
+
22
a2+
2a
+
2a
+
22
a2+
6a
+
32
(a+3)
(a+3)
a2+
3a
+
3a
+
22
(a+4)
(a+4)
a2+
4a
+
4a
+
42
a2+
8a
+
42
(a+b)2
=
__________=
______________=
__________.
a2+
2ab
+
b2
(a+b)
(a+b)
a2+
ab
+
ab
+
b2
(a+b)2
=
__________=
______________=
__________.
a2+
2ab
+
b2
(a+b)
(a+b)
a2+
ab
+
ab
+
b2
(a+b)2
=
a2+
2ab
+
b2
(a-b)2
=?
将“b”换做“-b”,试试看
[a
+
(-b)]2
=
a2
+
2a(-b)
+
(-b)2
=
a2-2ab
+
b2
(a-b)2
=
a2-2ab
+
b2
完全平方公式
两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
(a+b)2
=
a2+
2ab
+
b2
(a-b)2
=
a2-2ab
+
b2
4.公式中的字母
a,b
可以表示数,单项式和多项式。
1.积为二次三项式;
2.首项、末项为两数的平方和;
3.另一项是两数积的
2
倍,且与乘式中间的符号相同。
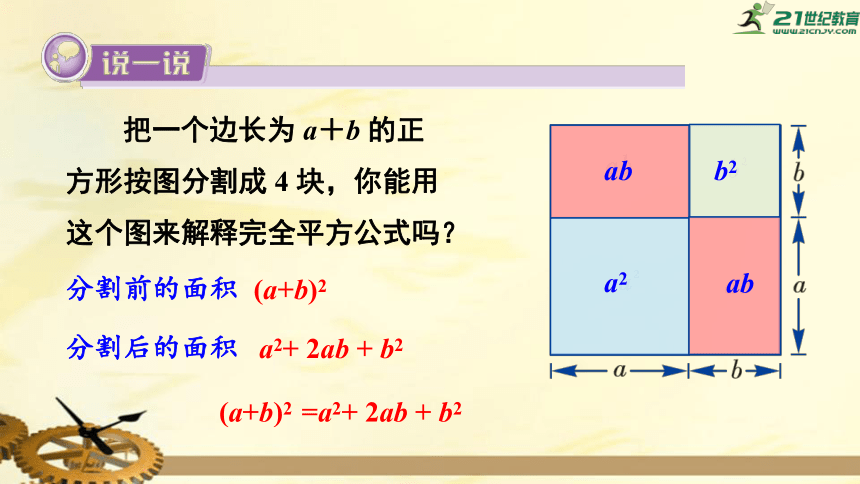
把一个边长为
a+b
的正方形按图分割成
4
块,你能用这个图来解释完全平方公式吗?
(a+b)2
a2+
2ab
+
b2
分割前的面积
分割后的面积
ab
b2
a2
ab
(a+b)2
=a2+
2ab
+
b2
运用完全平方公式计算:
(1)(3m+n)2
;
解:(1)(3m
+
n)2
=
(
3m
)2
+
2·3m·n
+
n2
=
9m2
+
6mn
+
n2
(2)
.
(2)
=
x2
-
2·x·
+
=
x2
-
x
+
随堂练习
1.下面各式的计算对不对?
如果不对,
应怎样改正?
(1)
(
x+2
)
2=
x2+4
;
(2)
(-a-b
)2=
a2-2ab
+b2
.
解:(1)不对,应为
(
x+2
)
2=
x2+4x+4
;
(2)
(-a-b
)2=
(a+b)2
=a2+2ab+b2
.
2.运用完全平方公式计算:
(1)
(x+4)2;
(2)
(2a-3)2;
(3)(5m
-
)2
解:(1)
(x+4)2
=
x2+8x+16
(2)
(2a-3)2
=
(2a)2-2·2a·3+32
=
4a2-12a+9
(3)(5m-
)2
=
(5m)2-2·5m·
+
(
)2
=
25m2-5m+
3.自编两个可以利用完全平方公式计算的题,
并与同学交流解题过程.
巩固练习
1.填空题:
(x+3y)2=_____________;
x2+6xy+9y2
________=
y2
–
y
+
;
(y
–
)2
(______)2
=
9a2-______+16b2;
3a-4b
24ab
x2+10x+____=(x+_____)2;
25
5
(-x-y)_______=x2+2xy+y2.
(-x-y)
2.
下列各式中哪些可以运用完全平方公式计算(
)
A.
(a+b)(a+c)
B.
(x+y)(-y+x)
C.
(ab-3x)(-3x+ab)
D.
(-m-n)(m-n)
C
3.计算:
(
x
–
2y)2
(2)(2xy
+
x)2
(1)
解:原式=
(
x)2
-
2(
x)(2y)
+
(2y)2
=
x2
-
2xy
+
4y2
解:原式=
(2xy)2
+2(2xy)(
x)
+
(
x)2
=
4x2y2
+
x2y
+
x2
4.利用完全平方公式计算:
(1)(-1-2x)2;
解:原式
=
(-1)2
–
2×(-1)×(2x)+(2x)2
=
1+4x+4x2
(2)(-2x+1)2.
解:原式
=
(-2x)2
+
2(-2x)×1+12
=
4x2-4x
+
1
课堂小结
完全平方公式
(a+b)2
=
a2+
2ab
+
b2
(a-b)2
=
a2-2ab
+
b2
两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
完全平方公式
第2章
整式的乘法
湘教版·七年级数学下册
上课课件
学习目标
【知识与技能】
理解公式的本质,从不同的层次上理解完全平方公式,并会运用公式进行简单的计算,了解完全平方公式的几何背景.
【过程与方法】
经历探索完全平方公式的过程,并从推导过程中,培养学生观察、发现、归纳、概括、猜想等探究创新能力,发展逻辑推理能力和有条理的表达能力,培养学生的数形结合意识.
【情感态度】
在学习中使学生体会学习数学的乐趣,培养学习数学的信心,感受数学的内在美.
【教学重点】
1.
弄清完全平方公式的来源及其结构特点,用自己的语言说明公式及其特点。
2.会用完全平方公式进行运算.
【教学难点】
会用完全平方公式进行运算.
复习导入
同学们,前面我们学习了多项式乘多项式法则和合并同类项法则,你会计算下列各题吗?
(x+3)2
=
______________________,
(x-3)2
=
_______________________,
(x+3)
(x+3)
=
x2+6x+9
(x-3)
(x-3)
=
x2-6x+9
这些式子的左边和右边有什么规律?
(2m+3n)2=________________________________,
(2m-3n)2=______________________________.
(2m+3n)
(2m+3n)=4m2+12mn+9n2
(2m-3n)
(2m-3n)=4m2-12mn+9n2
探究新知
计算下列各式,你能发现什么规律?
(a+1)2
=
(a+1)
(a+1)
=
a2+
a
+
a
+
12
=
a2+
2a
+
12,
(a+2)2
=
__________=
______________
=
__________,
(a+3)2
=
__________=
______________
=
__________,
(a+4)2
=
__________=
______________=
__________.
(a+2)
(a+2)
a2+
4a
+
22
a2+
2a
+
2a
+
22
a2+
6a
+
32
(a+3)
(a+3)
a2+
3a
+
3a
+
22
(a+4)
(a+4)
a2+
4a
+
4a
+
42
a2+
8a
+
42
(a+b)2
=
__________=
______________=
__________.
a2+
2ab
+
b2
(a+b)
(a+b)
a2+
ab
+
ab
+
b2
(a+b)2
=
__________=
______________=
__________.
a2+
2ab
+
b2
(a+b)
(a+b)
a2+
ab
+
ab
+
b2
(a+b)2
=
a2+
2ab
+
b2
(a-b)2
=?
将“b”换做“-b”,试试看
[a
+
(-b)]2
=
a2
+
2a(-b)
+
(-b)2
=
a2-2ab
+
b2
(a-b)2
=
a2-2ab
+
b2
完全平方公式
两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
(a+b)2
=
a2+
2ab
+
b2
(a-b)2
=
a2-2ab
+
b2
4.公式中的字母
a,b
可以表示数,单项式和多项式。
1.积为二次三项式;
2.首项、末项为两数的平方和;
3.另一项是两数积的
2
倍,且与乘式中间的符号相同。
把一个边长为
a+b
的正方形按图分割成
4
块,你能用这个图来解释完全平方公式吗?
(a+b)2
a2+
2ab
+
b2
分割前的面积
分割后的面积
ab
b2
a2
ab
(a+b)2
=a2+
2ab
+
b2
运用完全平方公式计算:
(1)(3m+n)2
;
解:(1)(3m
+
n)2
=
(
3m
)2
+
2·3m·n
+
n2
=
9m2
+
6mn
+
n2
(2)
.
(2)
=
x2
-
2·x·
+
=
x2
-
x
+
随堂练习
1.下面各式的计算对不对?
如果不对,
应怎样改正?
(1)
(
x+2
)
2=
x2+4
;
(2)
(-a-b
)2=
a2-2ab
+b2
.
解:(1)不对,应为
(
x+2
)
2=
x2+4x+4
;
(2)
(-a-b
)2=
(a+b)2
=a2+2ab+b2
.
2.运用完全平方公式计算:
(1)
(x+4)2;
(2)
(2a-3)2;
(3)(5m
-
)2
解:(1)
(x+4)2
=
x2+8x+16
(2)
(2a-3)2
=
(2a)2-2·2a·3+32
=
4a2-12a+9
(3)(5m-
)2
=
(5m)2-2·5m·
+
(
)2
=
25m2-5m+
3.自编两个可以利用完全平方公式计算的题,
并与同学交流解题过程.
巩固练习
1.填空题:
(x+3y)2=_____________;
x2+6xy+9y2
________=
y2
–
y
+
;
(y
–
)2
(______)2
=
9a2-______+16b2;
3a-4b
24ab
x2+10x+____=(x+_____)2;
25
5
(-x-y)_______=x2+2xy+y2.
(-x-y)
2.
下列各式中哪些可以运用完全平方公式计算(
)
A.
(a+b)(a+c)
B.
(x+y)(-y+x)
C.
(ab-3x)(-3x+ab)
D.
(-m-n)(m-n)
C
3.计算:
(
x
–
2y)2
(2)(2xy
+
x)2
(1)
解:原式=
(
x)2
-
2(
x)(2y)
+
(2y)2
=
x2
-
2xy
+
4y2
解:原式=
(2xy)2
+2(2xy)(
x)
+
(
x)2
=
4x2y2
+
x2y
+
x2
4.利用完全平方公式计算:
(1)(-1-2x)2;
解:原式
=
(-1)2
–
2×(-1)×(2x)+(2x)2
=
1+4x+4x2
(2)(-2x+1)2.
解:原式
=
(-2x)2
+
2(-2x)×1+12
=
4x2-4x
+
1
课堂小结
完全平方公式
(a+b)2
=
a2+
2ab
+
b2
(a-b)2
=
a2-2ab
+
b2
两数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
