第2章 整式的乘法 小结与复习 课件(共26张PPT)
文档属性
| 名称 | 第2章 整式的乘法 小结与复习 课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
小结与复习
第2章
整式的乘法
湘教版·七年级数学下册
上课课件
学习目标
【知识与技能】
梳理本章内容,构建知识网络;重点加强对整式的概念,整式的乘法运算,幂的运算性质的复习,并能灵活运用知识解决问题.
【过程与方法】
通过梳理本章内容,发展学生的符号感以及合情说理的能力,渗透转化、类比的思想.
【情感态度】
让学生在数学活动中通过相互间的合作与交流,进一步发展学生合作交流的能力和数学表达能力.感受数学与现实生活的密切联系,增强学生的数学应用意识.
【教学重点】
整式的乘法、幂的运算.
【教学难点】
整式的乘法、幂的运算.
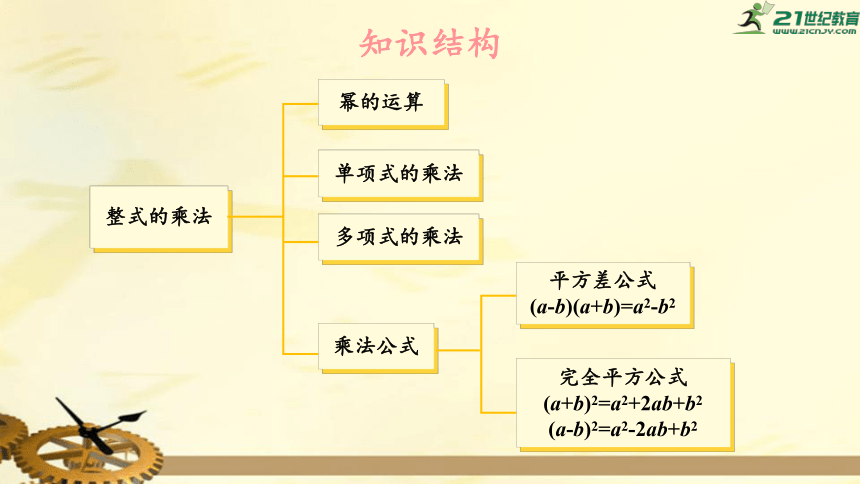
知识结构
整式的乘法
幂的运算
单项式的乘法
多项式的乘法
乘法公式
平方差公式
(a-b)(a+b)=a2-b2
完全平方公式
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
释疑解惑
1.
幂的运算性质
(1)同底数幂的乘法:
am·an
=
am+n
逆用:
am+n
=
am·an
(2)幂的乘方:
(am)n
=
amn
逆用:
amn
=
(am)n
(3)积的乘方:
(ab)n
=
anbn
逆用:
anbn
=
(ab)n
2.整式的乘除法:
(1)单项式乘单项式:
法则:单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余的字母连同它的指数不变,作为积的因式.
2.整式的乘除法:
(2)单项式乘多项式:
m(a
+
b
+
c)
=
ma
+
mb
+
mc
法则:单项式与多项式相乘,就是根据分配律用单项式去乘多项式的每一项,再把所得的积相加.
2.整式的乘除法:
(3)多项式乘多项式:
(a
+
b)(m
+
n)
=
am
+
an
+
bm
+
bn
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
3.整式乘法公式:
(1)
平方差公式:
(a+b)(a-b)
=
a?-b?
(a+b)2
=
(2)完全平方公式:
a?-2ab+b?
a?+2ab+b?
(a-b)?
=
逆用:
a?+2ab+b?
=(a+b)2
a?-2ab+b?
=(a-b)?
典例精析
1.下列运算正确的是
(
)
A.
x3+x3
=
x6
B.
2x·3x2
=
6x3
C.
(2x)3
=
6x3
D.
(2x2+x)÷x
=
2x
解析:A.应为
x3
+
x3
=
2x3,故本选项错误;B.
2x
·
3x2
=
6x3,
正确;C.应为(2x)3
=
23x3
=
8x3,故本选项错误;D.应为
(2x2
+
x)÷x
=
2x
+
1,故本选项错误.
B
2.已知
a=8131,b=2741,c=961,则
a,b,c
的大小关系是
(
)
A.
a>b>c
B.
a>c>b
C.
aD.
b>c>a
解析:因为a
=
813
=
(34)31
=
3124;
b
=
2741
=
(33)41
=
3123;
c
=
961
=
(32)61
=
3122.
则
a
>
b
>
c.
故选
A.
A
3.
一个长方体的长、宽、高分别
3a-4,
2a,
a,
它的体积等于(
)
A.
3a3-4a2
B.
a2
C.
6a3-8a2
D.
6a3-8a
解析:由题意知,V长方形
=
(3a-4)×2a×a=6a3-8a2.故选
C.
C
4.
已知:2x
=
4y+1,
27y
=
3x-1,
则
x-y
=______.
解析:因为
2x
=
4y+1,
所以
2x=2(2y+2),所以
x
=
2y+2
①
又因为
27x
=
3x-1,所以
33y
=
3x-1,所以
3y
=
x-1
②
解①②组成的方程组得
所以
x-y
=
3.
x
=
4
y
=
1
3
5.
计算:
(1)82×42010×(-0.25)2014;
解:82×42010×(-0.25)2014
=
43×42010×(-0.25)2014
=
42013×(-0.25)2013×(-0.25)
=
-0.25×
(-4×0.25)2013
=
5.
计算:
(2)20142
-
2013×2015;
解:20142
-
2013×2015
=
20142
-
(2014
-
1)(2014
+
1)
=
20142-(20142
-
12)
=
20142
-
20142
+
1
=
1
6.
先化简,再求值:(a2b-2ab2-b3)÷b-(a+b)(a-b),其中
a
=
,
b
=
-1.
解:
(a2b-2ab2-b3)÷b-(a+b)(a-b)
=
a2-2ab-b2-(a2-b2)
=
a2-2ab-b2-a2+b2
=
-2ab
当
a
=
,
b
=
-1
时,
原式
=
-2×
×(-1)
=
1.
7.
若
(x+y)2
=
36
,
(x-y)2
=
16
,求
xy、x2
+
y2
的值.
解:因为
(x+y)2
=
36
,
(x-y)2
=
16,
所以
x2
+
2xy
+
y2
=
36
①,
x2
-
2xy
+
y2
=
16
②,
①-②
得
4xy
=
20,
所以
xy
=
5,
①+②
得
2(x2+y2)
=
52,
所以
x2+y2
=
26.
巩固提高
1.已知:a+b=m,ab=-4,化简:(a-2)(b-2)
的结果是(
)
A.
6
B.
2m-8
C.
2m
D.
-2m
解析:因为a+b
=
m,ab
=
-4,
所以
(a-2)(b-2)
=
ab
+
4-2(a+b)
=
-4+4-2m
=
-2m.
故选D.
D
2.
某商场四月份售出某品牌衬衣
b
件,每件
c
元,营业额a
元.
五月份采取促销活动,售出该品牌衬衣
3b
件,每件打八折,则五月份该品牌衬衣的营业额比四月份增加(
)
A.
1.4a
元
B.
2.4a
元
C.
3.4a
元
D.
4.4a
元
解析:5月份营业额为
4月份营业额为
bc
=
a,
所以
a-a
=
1.4a.
A
3.
已知
(x+a)(x+b)
=
x2-13x
+
36,则
a
+
b
的值是
(
)
A.
13
B.
-13
C.
36
D.
-36
解:(x
+
a)(x
+
b)
=
x2
+
(a+b)x
+
ab,
又因为(x
+
a)(x
+
b)
=
x2-13x
+
36,所以
a+b
=
-13.
故选B.
B
4.
若
(a+2)2
+
|
b+1|
=
0,则
5ab2
–{2a2b-[3ab2-(4ab2-2a2b)]}
=
______.
解析:由
(a+2)2
+
|
b+1
|
=
0
得
a
=
-2,
b
=
-1,
当
a
=
-2,
b
=
-1
时,
5ab2
–
{2a2b
-
[3ab2
-
(4ab2
-
2a2b)]}
=
4ab2
=
-8.
-8
5.
计算:
解:根据幂的乘方与积的乘方法则可知,
原式
=
6.
已知
,求
的值.
解:因为
=
4,
所以
+
2
=
16,
所以
=
14.
7.
先化简:(2x-1)2
-
(3x+1)(3x-1)
+
5x(x-1),
再选取一个你喜欢的数代替
x
求值.
解:(2x
-
1)2
-
(3x
+
1)(3x
-
1)
+
5x(x
-
1)
=
4x2
-
4x
+
1
-
(9x2
-
1)
+
5x2
-
5x
=
4x2
-
4x
+
1
-
9x2
+
1
+
5x2
-
5x
=
-9x
+
2
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
小结与复习
第2章
整式的乘法
湘教版·七年级数学下册
上课课件
学习目标
【知识与技能】
梳理本章内容,构建知识网络;重点加强对整式的概念,整式的乘法运算,幂的运算性质的复习,并能灵活运用知识解决问题.
【过程与方法】
通过梳理本章内容,发展学生的符号感以及合情说理的能力,渗透转化、类比的思想.
【情感态度】
让学生在数学活动中通过相互间的合作与交流,进一步发展学生合作交流的能力和数学表达能力.感受数学与现实生活的密切联系,增强学生的数学应用意识.
【教学重点】
整式的乘法、幂的运算.
【教学难点】
整式的乘法、幂的运算.
知识结构
整式的乘法
幂的运算
单项式的乘法
多项式的乘法
乘法公式
平方差公式
(a-b)(a+b)=a2-b2
完全平方公式
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
释疑解惑
1.
幂的运算性质
(1)同底数幂的乘法:
am·an
=
am+n
逆用:
am+n
=
am·an
(2)幂的乘方:
(am)n
=
amn
逆用:
amn
=
(am)n
(3)积的乘方:
(ab)n
=
anbn
逆用:
anbn
=
(ab)n
2.整式的乘除法:
(1)单项式乘单项式:
法则:单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余的字母连同它的指数不变,作为积的因式.
2.整式的乘除法:
(2)单项式乘多项式:
m(a
+
b
+
c)
=
ma
+
mb
+
mc
法则:单项式与多项式相乘,就是根据分配律用单项式去乘多项式的每一项,再把所得的积相加.
2.整式的乘除法:
(3)多项式乘多项式:
(a
+
b)(m
+
n)
=
am
+
an
+
bm
+
bn
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
3.整式乘法公式:
(1)
平方差公式:
(a+b)(a-b)
=
a?-b?
(a+b)2
=
(2)完全平方公式:
a?-2ab+b?
a?+2ab+b?
(a-b)?
=
逆用:
a?+2ab+b?
=(a+b)2
a?-2ab+b?
=(a-b)?
典例精析
1.下列运算正确的是
(
)
A.
x3+x3
=
x6
B.
2x·3x2
=
6x3
C.
(2x)3
=
6x3
D.
(2x2+x)÷x
=
2x
解析:A.应为
x3
+
x3
=
2x3,故本选项错误;B.
2x
·
3x2
=
6x3,
正确;C.应为(2x)3
=
23x3
=
8x3,故本选项错误;D.应为
(2x2
+
x)÷x
=
2x
+
1,故本选项错误.
B
2.已知
a=8131,b=2741,c=961,则
a,b,c
的大小关系是
(
)
A.
a>b>c
B.
a>c>b
C.
a
b>c>a
解析:因为a
=
813
=
(34)31
=
3124;
b
=
2741
=
(33)41
=
3123;
c
=
961
=
(32)61
=
3122.
则
a
>
b
>
c.
故选
A.
A
3.
一个长方体的长、宽、高分别
3a-4,
2a,
a,
它的体积等于(
)
A.
3a3-4a2
B.
a2
C.
6a3-8a2
D.
6a3-8a
解析:由题意知,V长方形
=
(3a-4)×2a×a=6a3-8a2.故选
C.
C
4.
已知:2x
=
4y+1,
27y
=
3x-1,
则
x-y
=______.
解析:因为
2x
=
4y+1,
所以
2x=2(2y+2),所以
x
=
2y+2
①
又因为
27x
=
3x-1,所以
33y
=
3x-1,所以
3y
=
x-1
②
解①②组成的方程组得
所以
x-y
=
3.
x
=
4
y
=
1
3
5.
计算:
(1)82×42010×(-0.25)2014;
解:82×42010×(-0.25)2014
=
43×42010×(-0.25)2014
=
42013×(-0.25)2013×(-0.25)
=
-0.25×
(-4×0.25)2013
=
5.
计算:
(2)20142
-
2013×2015;
解:20142
-
2013×2015
=
20142
-
(2014
-
1)(2014
+
1)
=
20142-(20142
-
12)
=
20142
-
20142
+
1
=
1
6.
先化简,再求值:(a2b-2ab2-b3)÷b-(a+b)(a-b),其中
a
=
,
b
=
-1.
解:
(a2b-2ab2-b3)÷b-(a+b)(a-b)
=
a2-2ab-b2-(a2-b2)
=
a2-2ab-b2-a2+b2
=
-2ab
当
a
=
,
b
=
-1
时,
原式
=
-2×
×(-1)
=
1.
7.
若
(x+y)2
=
36
,
(x-y)2
=
16
,求
xy、x2
+
y2
的值.
解:因为
(x+y)2
=
36
,
(x-y)2
=
16,
所以
x2
+
2xy
+
y2
=
36
①,
x2
-
2xy
+
y2
=
16
②,
①-②
得
4xy
=
20,
所以
xy
=
5,
①+②
得
2(x2+y2)
=
52,
所以
x2+y2
=
26.
巩固提高
1.已知:a+b=m,ab=-4,化简:(a-2)(b-2)
的结果是(
)
A.
6
B.
2m-8
C.
2m
D.
-2m
解析:因为a+b
=
m,ab
=
-4,
所以
(a-2)(b-2)
=
ab
+
4-2(a+b)
=
-4+4-2m
=
-2m.
故选D.
D
2.
某商场四月份售出某品牌衬衣
b
件,每件
c
元,营业额a
元.
五月份采取促销活动,售出该品牌衬衣
3b
件,每件打八折,则五月份该品牌衬衣的营业额比四月份增加(
)
A.
1.4a
元
B.
2.4a
元
C.
3.4a
元
D.
4.4a
元
解析:5月份营业额为
4月份营业额为
bc
=
a,
所以
a-a
=
1.4a.
A
3.
已知
(x+a)(x+b)
=
x2-13x
+
36,则
a
+
b
的值是
(
)
A.
13
B.
-13
C.
36
D.
-36
解:(x
+
a)(x
+
b)
=
x2
+
(a+b)x
+
ab,
又因为(x
+
a)(x
+
b)
=
x2-13x
+
36,所以
a+b
=
-13.
故选B.
B
4.
若
(a+2)2
+
|
b+1|
=
0,则
5ab2
–{2a2b-[3ab2-(4ab2-2a2b)]}
=
______.
解析:由
(a+2)2
+
|
b+1
|
=
0
得
a
=
-2,
b
=
-1,
当
a
=
-2,
b
=
-1
时,
5ab2
–
{2a2b
-
[3ab2
-
(4ab2
-
2a2b)]}
=
4ab2
=
-8.
-8
5.
计算:
解:根据幂的乘方与积的乘方法则可知,
原式
=
6.
已知
,求
的值.
解:因为
=
4,
所以
+
2
=
16,
所以
=
14.
7.
先化简:(2x-1)2
-
(3x+1)(3x-1)
+
5x(x-1),
再选取一个你喜欢的数代替
x
求值.
解:(2x
-
1)2
-
(3x
+
1)(3x
-
1)
+
5x(x
-
1)
=
4x2
-
4x
+
1
-
(9x2
-
1)
+
5x2
-
5x
=
4x2
-
4x
+
1
-
9x2
+
1
+
5x2
-
5x
=
-9x
+
2
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
