2.2.2 探索直线平行的条件—内错角、同旁内角课件(共26张PPT)
文档属性
| 名称 | 2.2.2 探索直线平行的条件—内错角、同旁内角课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 634.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 23:39:50 | ||
图片预览





文档简介
第二章 相交线与平行线
内错角、同旁内角内错角、同旁内角
经历观察、操作、想象、推理、交流等活动,并能积极、主动地进行自主探索或与同伴交流.
知识目标:
经历探索直线平行的过程,掌握直线平行的条件,并能解决一些简单的实际问题.
能力目标:
通过实际操作、讨论、交流,识别“内错角”和“同旁内角”,并利用“内错角相等,两直线平行”和“同旁内角互补,两直线平行”解题.
情感目标:
学习目标
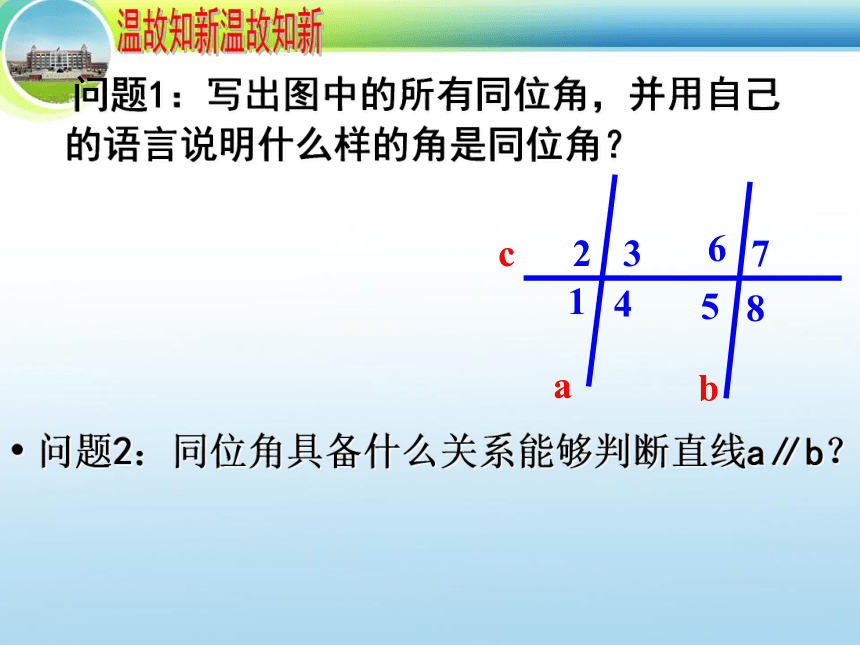
问题1:写出图中的所有同位角,并用自己的语言说明什么样的角是同位角?
温故知新温故知新
a
b
c
1
2
3
4
5
6
7
8
问题2:同位角具备什么关系能够判断直线a∥b?
小明有一块小画板,他想知道它的上下边缘是否平行,你能帮帮他吗?
问题:
动脑筋动脑筋
能利用同位角相等两直线平行的结论来说明吗?
⌒
1
⌒
2
⌒
3
⌒
4
图形中有同位角吗?有的话请你指出来.
4
2
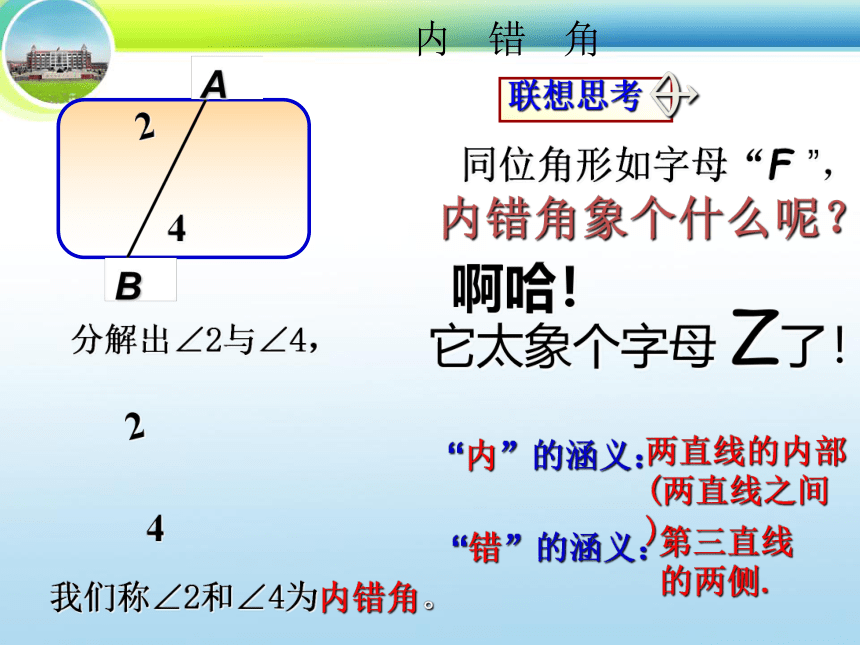
分解出∠2与∠4,
2
4
内错角象个什么呢?
啊哈!
我们称∠2和∠4为内错角。
?
联想思考
同位角形如字母“F ”,
它太象个字母 Z了!
内 错 角
“内”的涵义:
两直线的内部(两直线之间);
“错”的涵义:
第三直线的两侧.
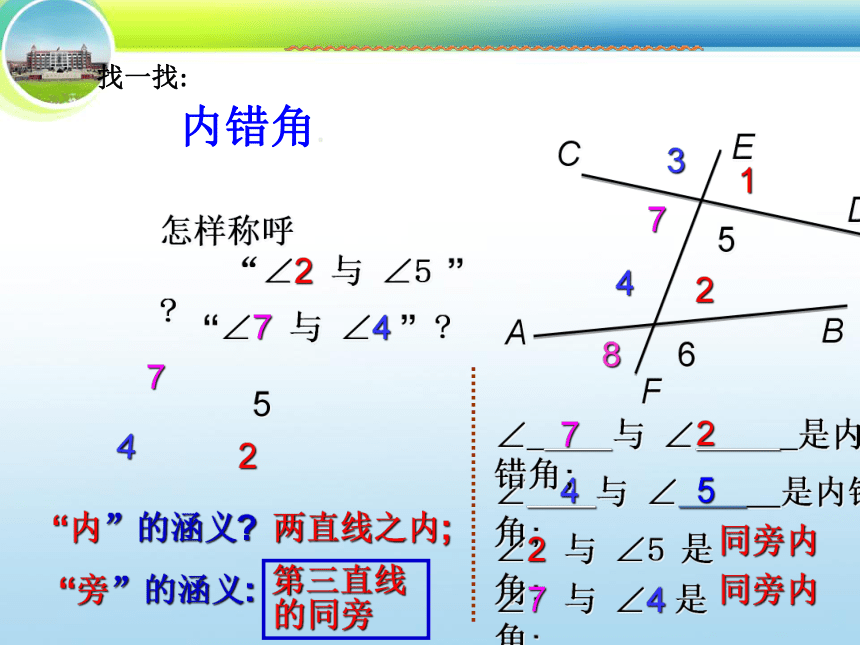
找一找: 如图“三线八角”中的
内错角.
F
1
3
7
5
2
8
6
D
C
A
B
E
4
7
2
∠ 与 ∠ 是内错角;
4
5
∠ 与 ∠ 是内错角;
5
2
7
4
∠2 与 ∠5 是 角;
∠7 与 ∠4 是 角;
同旁内
同旁内
“内”的涵义?
“旁”的涵义:
两直线之内;
怎样称呼
“∠2 与 ∠5 ” ?
“∠7 与 ∠4 ” ?
第三直线的同旁
“三线八角” 小结
两直线被第三直线所截,
F
1
3
7
5
2
8
6
D
C
A
B
E
4
构成的八个角中,
① 位于两直线同一方、
② 位于两直线的 ,
且在第三直线的 的
两个角, 叫做 内错角 ;
且在第三直线同一侧的
两个角,叫做 ;
同位角
内部
两侧
③ 位于两直线的 ,
且在第三直线的 的
两个角, 叫做 同旁内角 ;
内部
同旁
同位角是 F 形状
内错角是 形状
Z
同旁内角是 形状
U
议一议:
1.内错角满足什么关系时,两直线平行?
2.同旁内角满足什么关系时,两直线平行?
c
a
b
1
2
3
4
5
6
7
8
新知探究
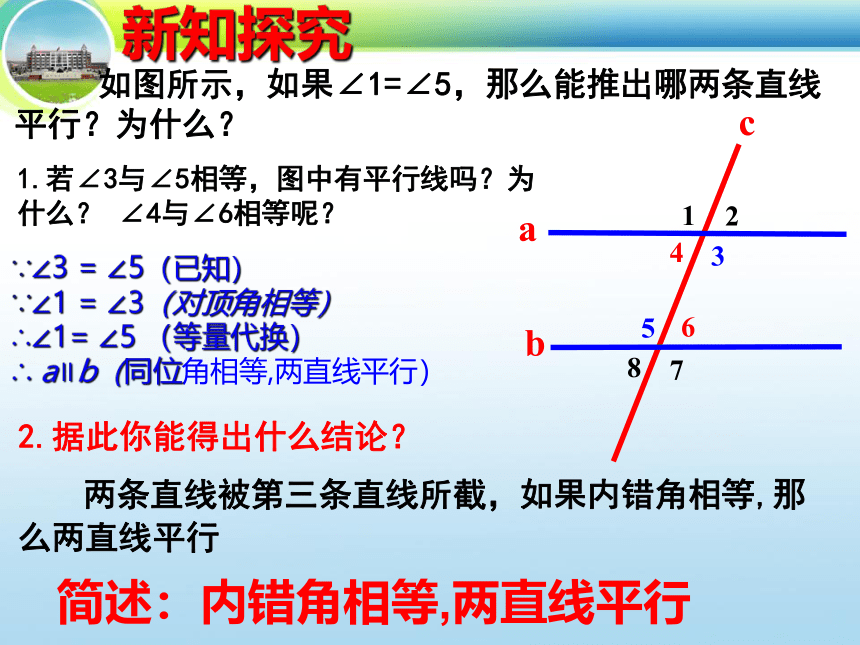
如图所示,如果∠1=∠5,那么能推出哪两条直线平行?为什么?
1.若∠3与∠5相等,图中有平行线吗?为什么? ∠4与∠6相等呢?
∵∠3 = ∠5(已知)
∵∠1 = ∠3(对顶角相等)
∴∠1= ∠5 (等量代换)
∴ a∥b(同位角相等,两直线平行)
简述:内错角相等,两直线平行
两条直线被第三条直线所截,如果内错角相等,那么两直线平行
2.据此你能得出什么结论?
c
a
b
1
2
3
4
5
6
7
8
新知探究
如果∠4与∠5互为补角,图中有平行线吗?为什么? ∠3与∠6互补呢?
∵ ∠4 、 ∠5互补 ( 已知 )
又∵ ∠4 、 ∠1互补(补角定义)
∴ ∠1=∠5 (
∴ a∥b( 同位角相等,两直线平行)
简述:同旁内角互补,两直线平行
两条直线被第三条直线所截,如果同旁内角互补,那么两直线平行
据此你能得出什么结论?
同角的补角相等)
简述:同位角相等,两直线平行
判定两条直线平行的方法小结:
1.两条直线被第三条直线所截,如果同位角相等,那么两直线平行
简述:内错角相等,两直线平行
2.两条直线被第三条直线所截,如果内错角相等,那么两直线平行
简述:同旁内角互补,两直线平行
3.两条直线被第三条直线所截,如果同旁内角互补,那么两直线平行
4.平面内,不相交的两直线平行
5.平行于同一条直线的两条直线互相平行
内错角相等,两直线平行
符号语言
∵∠1=∠2
∴ a∥b
c
1
2
a
b
(内错角相等,两直线平行)
c
1
2
a
b
同旁内角互补,两直线平行
∵∠1+∠2=1800
∴ a∥b
(同旁内角互补,两直线平行)
1. 观察右图并填空:
∠1 与 是同位角;
∠5 与 是同旁内角;
(3)∠1 与 是内错角.
∠4
∠3
∠2
m
b
a
n
2
3
1
4
5
随堂练习
1.图中各角分别满足下列条件时,你能判断哪两条直线平行吗?
①∠1=∠4 ②∠2=∠4 ③∠1+∠3=180°
a
b
l
m
n
1
2
3
4
a∥b.
l∥m.
l∥n .
随堂练习
?2.看图填空:(1)如右图,
∵∠1=∠2 (已知)
∴ ∥ ( ),
∵∠2=__ ,(已知)
∴ ∥FG,
∴AC∥FG.( )
1
2
3
4
A
B
C
D
E
F
G
随堂练习
内错角相等,两直线平行
CA
DE
∠4
DE
平行于同一条直线的两直线平行
做一做
如图,三个相同的三角尺拼接成一个图形,请找出图中所有的平行线,并说明你判断的理由.
BC∥AE(或CD∥AE或BD∥AE)
BA∥CE
CA∥DE
1
2
1
做一做
如图,三个相同的三角尺拼接成一个图形,请找出图中所有的平行线,并说明你判断的理由.
BC∥AE(或CD∥AE或BD∥AE)
BA∥CE
CA∥DE
1
2
做一做
如图,三个相同的三角尺拼接成一个图形,请找出图中所有的平行线,并说明你判断的理由.
BC∥AE(或CD∥AE或BD∥AE)
BA∥CE
CA∥DE
1
2
2
1
2
做一做
如图,三个相同的三角尺拼接成一个图形,请找出图中所有的平行线,并说明你判断的理由.
BC∥AE(或CD∥AE或BD∥AE)
BA∥CE
CA∥DE
2
1
做一做
如图,三个相同的三角尺拼接成一个图形,请找出图中所有的平行线,并说明你判断的理由.
BC∥AE(或CD∥AE或BD∥AE)
BA∥CE
CA∥DE
小明有一块小画板,他想知道它的上下边缘是否平行,你能帮帮他吗?
问题:
小明只有一个量角器,他通过测量某些角的大小就能知道这个画板的上下边缘是否平行,你知道他是怎样做的吗?
⌒
1
⌒
2
⌒
3
⌒
4
学以致用
例:如图∠1=∠2,∠B+∠BDE= 180°,图中那些线互相平行,为什么?
精例赏析
变式训练
(1) ∠2与哪个角相等时, DE∥BC?
(2) ∠A与哪个角相等时, AB∥EF?
? 看图填空:
(2)如右图,∵ ∠2=( )
∴DE∥BC ,
∵ ∠B+ =180°,
∴ DB ∥EF
∵ ∠B+ ∠5 =180 °
∴ ∥ .
A
B
C
D
E
F
4
3
2
1
5
达标检测
颗粒归仓颗粒归仓
4
1
2
3
5
6
7
8
D
C
B
E
A
F
1. 再识“三线八角”:
4对同位角
∠1和∠5,
∠2和∠6,
∠3和∠7,
∠4和∠8.
2对内错角
∠3和∠5,
∠6和∠4.
2对同旁内角
∠5和∠4,
∠3和∠6.
颗粒归仓颗粒归仓
2. 两直线平行的条件
① 同位角相等,两直线平行;
② 内错角相等,两直线平行;
③ 同旁内角互补,两直线平行.
3. 本节课运用了哪些数学思想方法?
你有什么收获?
内错角、同旁内角内错角、同旁内角
经历观察、操作、想象、推理、交流等活动,并能积极、主动地进行自主探索或与同伴交流.
知识目标:
经历探索直线平行的过程,掌握直线平行的条件,并能解决一些简单的实际问题.
能力目标:
通过实际操作、讨论、交流,识别“内错角”和“同旁内角”,并利用“内错角相等,两直线平行”和“同旁内角互补,两直线平行”解题.
情感目标:
学习目标
问题1:写出图中的所有同位角,并用自己的语言说明什么样的角是同位角?
温故知新温故知新
a
b
c
1
2
3
4
5
6
7
8
问题2:同位角具备什么关系能够判断直线a∥b?
小明有一块小画板,他想知道它的上下边缘是否平行,你能帮帮他吗?
问题:
动脑筋动脑筋
能利用同位角相等两直线平行的结论来说明吗?
⌒
1
⌒
2
⌒
3
⌒
4
图形中有同位角吗?有的话请你指出来.
4
2
分解出∠2与∠4,
2
4
内错角象个什么呢?
啊哈!
我们称∠2和∠4为内错角。
?
联想思考
同位角形如字母“F ”,
它太象个字母 Z了!
内 错 角
“内”的涵义:
两直线的内部(两直线之间);
“错”的涵义:
第三直线的两侧.
找一找: 如图“三线八角”中的
内错角.
F
1
3
7
5
2
8
6
D
C
A
B
E
4
7
2
∠ 与 ∠ 是内错角;
4
5
∠ 与 ∠ 是内错角;
5
2
7
4
∠2 与 ∠5 是 角;
∠7 与 ∠4 是 角;
同旁内
同旁内
“内”的涵义?
“旁”的涵义:
两直线之内;
怎样称呼
“∠2 与 ∠5 ” ?
“∠7 与 ∠4 ” ?
第三直线的同旁
“三线八角” 小结
两直线被第三直线所截,
F
1
3
7
5
2
8
6
D
C
A
B
E
4
构成的八个角中,
① 位于两直线同一方、
② 位于两直线的 ,
且在第三直线的 的
两个角, 叫做 内错角 ;
且在第三直线同一侧的
两个角,叫做 ;
同位角
内部
两侧
③ 位于两直线的 ,
且在第三直线的 的
两个角, 叫做 同旁内角 ;
内部
同旁
同位角是 F 形状
内错角是 形状
Z
同旁内角是 形状
U
议一议:
1.内错角满足什么关系时,两直线平行?
2.同旁内角满足什么关系时,两直线平行?
c
a
b
1
2
3
4
5
6
7
8
新知探究
如图所示,如果∠1=∠5,那么能推出哪两条直线平行?为什么?
1.若∠3与∠5相等,图中有平行线吗?为什么? ∠4与∠6相等呢?
∵∠3 = ∠5(已知)
∵∠1 = ∠3(对顶角相等)
∴∠1= ∠5 (等量代换)
∴ a∥b(同位角相等,两直线平行)
简述:内错角相等,两直线平行
两条直线被第三条直线所截,如果内错角相等,那么两直线平行
2.据此你能得出什么结论?
c
a
b
1
2
3
4
5
6
7
8
新知探究
如果∠4与∠5互为补角,图中有平行线吗?为什么? ∠3与∠6互补呢?
∵ ∠4 、 ∠5互补 ( 已知 )
又∵ ∠4 、 ∠1互补(补角定义)
∴ ∠1=∠5 (
∴ a∥b( 同位角相等,两直线平行)
简述:同旁内角互补,两直线平行
两条直线被第三条直线所截,如果同旁内角互补,那么两直线平行
据此你能得出什么结论?
同角的补角相等)
简述:同位角相等,两直线平行
判定两条直线平行的方法小结:
1.两条直线被第三条直线所截,如果同位角相等,那么两直线平行
简述:内错角相等,两直线平行
2.两条直线被第三条直线所截,如果内错角相等,那么两直线平行
简述:同旁内角互补,两直线平行
3.两条直线被第三条直线所截,如果同旁内角互补,那么两直线平行
4.平面内,不相交的两直线平行
5.平行于同一条直线的两条直线互相平行
内错角相等,两直线平行
符号语言
∵∠1=∠2
∴ a∥b
c
1
2
a
b
(内错角相等,两直线平行)
c
1
2
a
b
同旁内角互补,两直线平行
∵∠1+∠2=1800
∴ a∥b
(同旁内角互补,两直线平行)
1. 观察右图并填空:
∠1 与 是同位角;
∠5 与 是同旁内角;
(3)∠1 与 是内错角.
∠4
∠3
∠2
m
b
a
n
2
3
1
4
5
随堂练习
1.图中各角分别满足下列条件时,你能判断哪两条直线平行吗?
①∠1=∠4 ②∠2=∠4 ③∠1+∠3=180°
a
b
l
m
n
1
2
3
4
a∥b.
l∥m.
l∥n .
随堂练习
?2.看图填空:(1)如右图,
∵∠1=∠2 (已知)
∴ ∥ ( ),
∵∠2=__ ,(已知)
∴ ∥FG,
∴AC∥FG.( )
1
2
3
4
A
B
C
D
E
F
G
随堂练习
内错角相等,两直线平行
CA
DE
∠4
DE
平行于同一条直线的两直线平行
做一做
如图,三个相同的三角尺拼接成一个图形,请找出图中所有的平行线,并说明你判断的理由.
BC∥AE(或CD∥AE或BD∥AE)
BA∥CE
CA∥DE
1
2
1
做一做
如图,三个相同的三角尺拼接成一个图形,请找出图中所有的平行线,并说明你判断的理由.
BC∥AE(或CD∥AE或BD∥AE)
BA∥CE
CA∥DE
1
2
做一做
如图,三个相同的三角尺拼接成一个图形,请找出图中所有的平行线,并说明你判断的理由.
BC∥AE(或CD∥AE或BD∥AE)
BA∥CE
CA∥DE
1
2
2
1
2
做一做
如图,三个相同的三角尺拼接成一个图形,请找出图中所有的平行线,并说明你判断的理由.
BC∥AE(或CD∥AE或BD∥AE)
BA∥CE
CA∥DE
2
1
做一做
如图,三个相同的三角尺拼接成一个图形,请找出图中所有的平行线,并说明你判断的理由.
BC∥AE(或CD∥AE或BD∥AE)
BA∥CE
CA∥DE
小明有一块小画板,他想知道它的上下边缘是否平行,你能帮帮他吗?
问题:
小明只有一个量角器,他通过测量某些角的大小就能知道这个画板的上下边缘是否平行,你知道他是怎样做的吗?
⌒
1
⌒
2
⌒
3
⌒
4
学以致用
例:如图∠1=∠2,∠B+∠BDE= 180°,图中那些线互相平行,为什么?
精例赏析
变式训练
(1) ∠2与哪个角相等时, DE∥BC?
(2) ∠A与哪个角相等时, AB∥EF?
? 看图填空:
(2)如右图,∵ ∠2=( )
∴DE∥BC ,
∵ ∠B+ =180°,
∴ DB ∥EF
∵ ∠B+ ∠5 =180 °
∴ ∥ .
A
B
C
D
E
F
4
3
2
1
5
达标检测
颗粒归仓颗粒归仓
4
1
2
3
5
6
7
8
D
C
B
E
A
F
1. 再识“三线八角”:
4对同位角
∠1和∠5,
∠2和∠6,
∠3和∠7,
∠4和∠8.
2对内错角
∠3和∠5,
∠6和∠4.
2对同旁内角
∠5和∠4,
∠3和∠6.
颗粒归仓颗粒归仓
2. 两直线平行的条件
① 同位角相等,两直线平行;
② 内错角相等,两直线平行;
③ 同旁内角互补,两直线平行.
3. 本节课运用了哪些数学思想方法?
你有什么收获?
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
