2020--2021学年沪科版七年级数学下册教案-10.3 平行线的性质
文档属性
| 名称 | 2020--2021学年沪科版七年级数学下册教案-10.3 平行线的性质 | 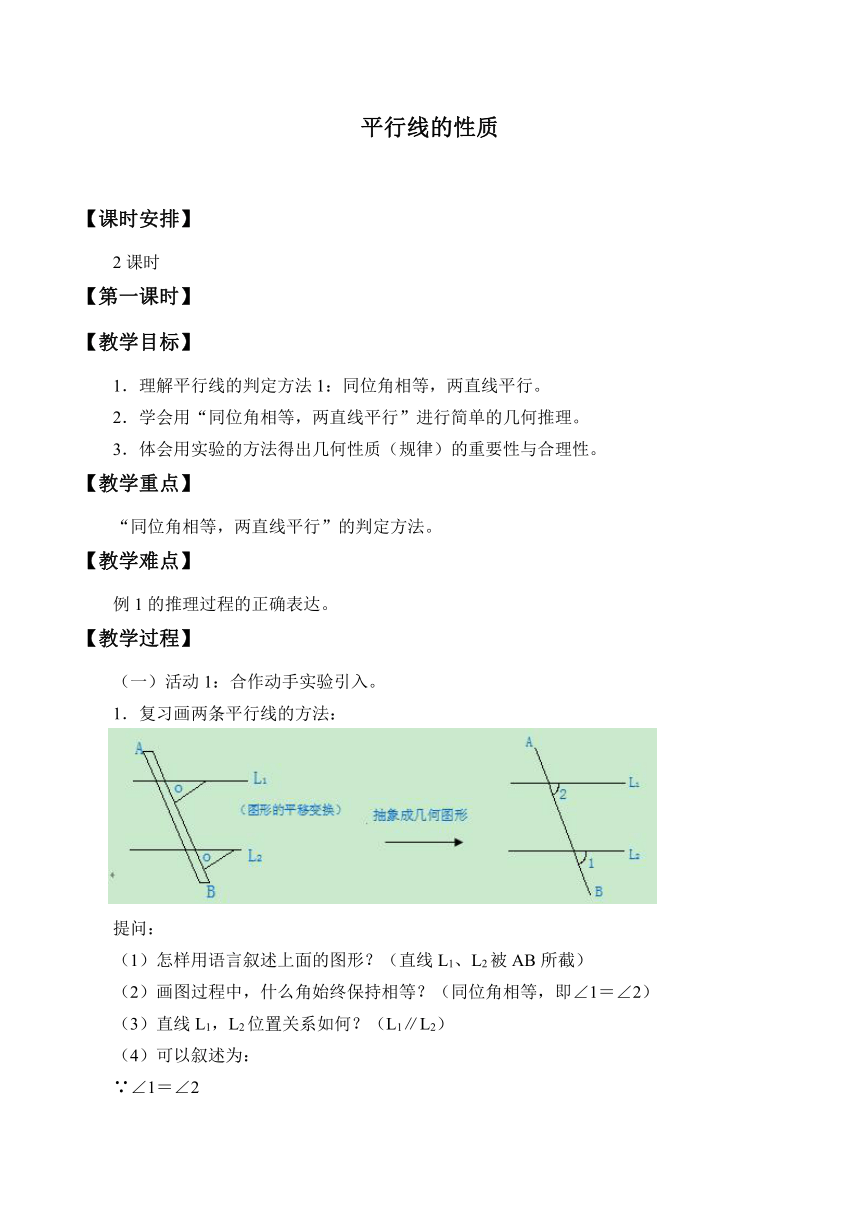 | |
| 格式 | zip | ||
| 文件大小 | 262.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 07:32:44 | ||
图片预览


文档简介
平行线的性质
【课时安排】
2课时
【第一课时】
【教学目标】
1.理解平行线的判定方法1:同位角相等,两直线平行。
2.学会用“同位角相等,两直线平行”进行简单的几何推理。
3.体会用实验的方法得出几何性质(规律)的重要性与合理性。
【教学重点】
“同位角相等,两直线平行”的判定方法。
【教学难点】
例1的推理过程的正确表达。
【教学过程】
(一)活动1:合作动手实验引入。
1.复习画两条平行线的方法:
提问:
(1)怎样用语言叙述上面的图形?(直线L1、L2被AB所截)
(2)画图过程中,什么角始终保持相等?(同位角相等,即∠1=∠2)
(3)直线L1,L2位置关系如何?(L1∥L2)
(4)可以叙述为:
∵∠1=∠2
∴L1∥L2
(?)
(二)活动2:平行线的判定方法1:
由上面,同学们你能发现判定两直线平行的方法吗?
语言叙述:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单地说:同位角相等,两直线平行。
几何叙述:
∵∠1=∠2
∴L1∥L2
(同位角相等,两直线平行)
(三)活动3:课堂练习:
(四)活动4:例题讲解
例:已知直线L1、L2被L3所截,如图,∠1=45°,∠2=135°,试判断L1与L2是否平行。并说明理由。
解:L1∥L2
理由如下:
∵∠2+∠3=180°,∠2=135°
∴∠3=180°-∠2=180°-135°=45°
∵∠1=45°
∴∠1=∠3
∴L1∥L2(同位角相等,两直线平行)
思路:
1.判定平行线方法。
2.图中有无同位角(注∠3位置)
3.能说明∠3=∠1吗?
4.结论。
5.∠3还可以是其它位置吗?你能说明L1∥L2吗?
(五)活动5:小结与反思
你学到了什么?
你认为还有什么不懂的?
你有什么经验与收获让同学们共享呢?
【第二课时】
【教学目标】
1.经历观察、操作、想象、推理、交流等活动,进一步发展空间观念,推理能力和有条理表达能力。
2.经历探索直线平行的性质的过程,掌握平行线的三条性质,并能用它们进行简单的推理和计算。
【教学重点】
平行线性质的研究和发现过程是本节课的重点。
【教学难点】
正确区分平行线的性质和判定是本节课的难点。
【教学过程】
(一)复习
1.请同学们先复习一下前面所学过的平行线的判定方法,并说出它们的已知和结论分别是什么?
2.把这三句话已知和结论颠倒一下,可得到怎样的语句?它们正确吗?
3.是不是原本正确的话,颠倒一下前后顺序,得到新的一句话,是否一定正确?试举例说明。
如、“若a=b,则a2=b2”是正确的,但“若a2=b2,则a=b”是错误的。又如“对顶角相等”是正确的。但“相等的角是对顶角”则是错误的。因此,原本正确的话将它倒过来说后,它不一定正确,此时它的正确与否要通过证明。
(二)新课
1.我们先看刚才得到的第一句话“两直线平行,同位角相等”。先在请同学们画两条平行线,然后画几条直线和平行线相交,用量角器测量一下,它们产生的几组同位角是否相等?
平行线的性质:
上一课时,我们学习的是“同位角相等,两直线平行”,此时,两直线是否平行是未知的,要我们通过同位角是否相等来判定,即是用来判定两条直线是否平行的,故我们称之为“两直线平行的判定公理”。而这句话“两直线平行,同位角相等”是已知“平行”从而得到“同位角相等”,因为平行是作为已知条件,因此,我们把这句话称为“平行线的性质公理”,即:两条平行线被第三条线所截,同位角相等。简单说成:两直线平行,同位角相等。
2.现在我们来用这个性质公理,来证明另两句话的正确性。
想想看,“两直线平行,内错角相等”这句话有哪些已知条件,由哪些图形组成?
已知:如图,直线a∥b
求证:
(1)∠1=∠4;
(2)∠1+∠2=180°
证明:∵a∥b(已知)
∴∠1=∠3(两直线平行,同位角相等)
又∵∠3=∠4(对顶角相等)
∴∠1=∠4
(2)∵a∥b(已知)
∴∠1=∠3(两直线平行,同位角相等)
又∵∠2+∠3=180°(邻补角的定义)
∴∠1+∠2=180°
思考:如何用(1)来证明(2)?
例1.已知:如图所示,点D、E、F分别在△ABC的边AB、AC、BC上,且DE∥BC,∠B=48°。
(1)试求∠ADE的度数;
(2)如果∠DEF=48°,那么EF与AB平行吗?
解:(1)∵DE∥BC
∴∠ADE=∠B=48°
(2)由(1),得∠ADE=48°
而∠DEF=48°,
∴∠ADE=∠DEF
∴EF∥AB
(三)练习
课本1、2、3
(四)小结
平行性质与判定的区别
【课时安排】
2课时
【第一课时】
【教学目标】
1.理解平行线的判定方法1:同位角相等,两直线平行。
2.学会用“同位角相等,两直线平行”进行简单的几何推理。
3.体会用实验的方法得出几何性质(规律)的重要性与合理性。
【教学重点】
“同位角相等,两直线平行”的判定方法。
【教学难点】
例1的推理过程的正确表达。
【教学过程】
(一)活动1:合作动手实验引入。
1.复习画两条平行线的方法:
提问:
(1)怎样用语言叙述上面的图形?(直线L1、L2被AB所截)
(2)画图过程中,什么角始终保持相等?(同位角相等,即∠1=∠2)
(3)直线L1,L2位置关系如何?(L1∥L2)
(4)可以叙述为:
∵∠1=∠2
∴L1∥L2
(?)
(二)活动2:平行线的判定方法1:
由上面,同学们你能发现判定两直线平行的方法吗?
语言叙述:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单地说:同位角相等,两直线平行。
几何叙述:
∵∠1=∠2
∴L1∥L2
(同位角相等,两直线平行)
(三)活动3:课堂练习:
(四)活动4:例题讲解
例:已知直线L1、L2被L3所截,如图,∠1=45°,∠2=135°,试判断L1与L2是否平行。并说明理由。
解:L1∥L2
理由如下:
∵∠2+∠3=180°,∠2=135°
∴∠3=180°-∠2=180°-135°=45°
∵∠1=45°
∴∠1=∠3
∴L1∥L2(同位角相等,两直线平行)
思路:
1.判定平行线方法。
2.图中有无同位角(注∠3位置)
3.能说明∠3=∠1吗?
4.结论。
5.∠3还可以是其它位置吗?你能说明L1∥L2吗?
(五)活动5:小结与反思
你学到了什么?
你认为还有什么不懂的?
你有什么经验与收获让同学们共享呢?
【第二课时】
【教学目标】
1.经历观察、操作、想象、推理、交流等活动,进一步发展空间观念,推理能力和有条理表达能力。
2.经历探索直线平行的性质的过程,掌握平行线的三条性质,并能用它们进行简单的推理和计算。
【教学重点】
平行线性质的研究和发现过程是本节课的重点。
【教学难点】
正确区分平行线的性质和判定是本节课的难点。
【教学过程】
(一)复习
1.请同学们先复习一下前面所学过的平行线的判定方法,并说出它们的已知和结论分别是什么?
2.把这三句话已知和结论颠倒一下,可得到怎样的语句?它们正确吗?
3.是不是原本正确的话,颠倒一下前后顺序,得到新的一句话,是否一定正确?试举例说明。
如、“若a=b,则a2=b2”是正确的,但“若a2=b2,则a=b”是错误的。又如“对顶角相等”是正确的。但“相等的角是对顶角”则是错误的。因此,原本正确的话将它倒过来说后,它不一定正确,此时它的正确与否要通过证明。
(二)新课
1.我们先看刚才得到的第一句话“两直线平行,同位角相等”。先在请同学们画两条平行线,然后画几条直线和平行线相交,用量角器测量一下,它们产生的几组同位角是否相等?
平行线的性质:
上一课时,我们学习的是“同位角相等,两直线平行”,此时,两直线是否平行是未知的,要我们通过同位角是否相等来判定,即是用来判定两条直线是否平行的,故我们称之为“两直线平行的判定公理”。而这句话“两直线平行,同位角相等”是已知“平行”从而得到“同位角相等”,因为平行是作为已知条件,因此,我们把这句话称为“平行线的性质公理”,即:两条平行线被第三条线所截,同位角相等。简单说成:两直线平行,同位角相等。
2.现在我们来用这个性质公理,来证明另两句话的正确性。
想想看,“两直线平行,内错角相等”这句话有哪些已知条件,由哪些图形组成?
已知:如图,直线a∥b
求证:
(1)∠1=∠4;
(2)∠1+∠2=180°
证明:∵a∥b(已知)
∴∠1=∠3(两直线平行,同位角相等)
又∵∠3=∠4(对顶角相等)
∴∠1=∠4
(2)∵a∥b(已知)
∴∠1=∠3(两直线平行,同位角相等)
又∵∠2+∠3=180°(邻补角的定义)
∴∠1+∠2=180°
思考:如何用(1)来证明(2)?
例1.已知:如图所示,点D、E、F分别在△ABC的边AB、AC、BC上,且DE∥BC,∠B=48°。
(1)试求∠ADE的度数;
(2)如果∠DEF=48°,那么EF与AB平行吗?
解:(1)∵DE∥BC
∴∠ADE=∠B=48°
(2)由(1),得∠ADE=48°
而∠DEF=48°,
∴∠ADE=∠DEF
∴EF∥AB
(三)练习
课本1、2、3
(四)小结
平行性质与判定的区别
