1.2 二次函数的图象与性质(第5课时) 二次函数y=ax^2+bx+c(a≠0)的图象与性质 课件(共22张PPT)
文档属性
| 名称 | 1.2 二次函数的图象与性质(第5课时) 二次函数y=ax^2+bx+c(a≠0)的图象与性质 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
二次函数
y
=
ax?
+
bx
+
c(a≠0)的图象与性质
湘教版·九年级数学下册
上课课件
第1章
二次函数
学习目标
【知识与技能】
1.会用描点法画二次函数y=ax2+bx+c的图象.
2.会用配方法求抛物线y=ax2+bx+c的顶点坐标、开口方向、对称轴、y随x的增减性.
3.能通过配方求出二次函数y=ax2+bx+c(a≠0)的最大或最小值;能利用二次函数的性质求实际问题中的最大值或最小值.
【过程与方法】
1.经历探索二次函数y=ax2+bx+c(a≠0)的图象的作法和性质的过程,体会建立二次函数y=ax2+bx+c(a≠0)对称轴和顶点坐标公式的必要性.
2.在学习y=ax2+bx+c(a≠0)的性质的过程中,渗透转化(化归)的思想.
【情感态度】
进一步体会由特殊到一般的化归思想,形成积极参与数学活动的意识.
【教学重点】
①用配方法求y=ax2+bx+c的顶点坐标;②会用描点法画y=ax2+bx+c的图象并能说出图象的性质.
【教学难点】
能利用二次函数y=ax2+bx+c(a≠0)的对称轴和顶点坐标公式,解决一些问题,能通过对称性画出二次函数y=ax2+bx+c(a≠0)的图象.
探究新知
画出
的图象.
配方:
故对称轴是直线
,
顶点坐标是
.
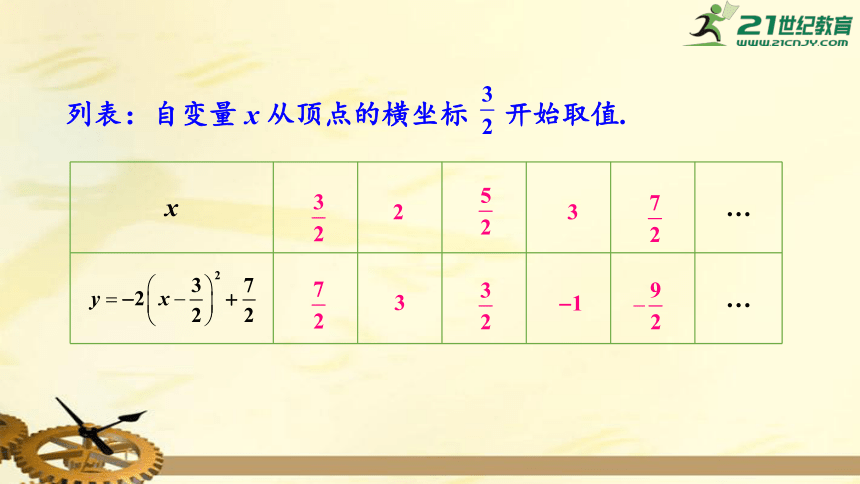
列表:自变量
x
从顶点的横坐标
开始取值.
x
…
…
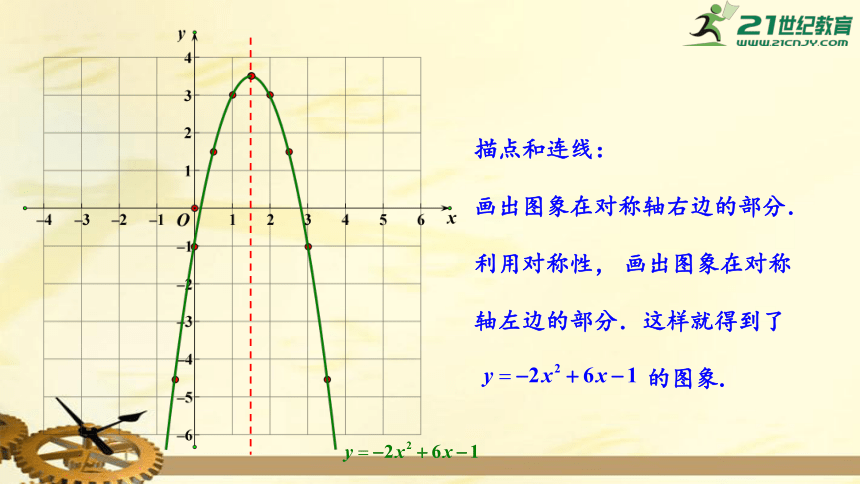
描点和连线:
画出图象在对称轴右边的部分.
利用对称性,
画出图象在对称轴左边的部分.这样就得到了
的图象.
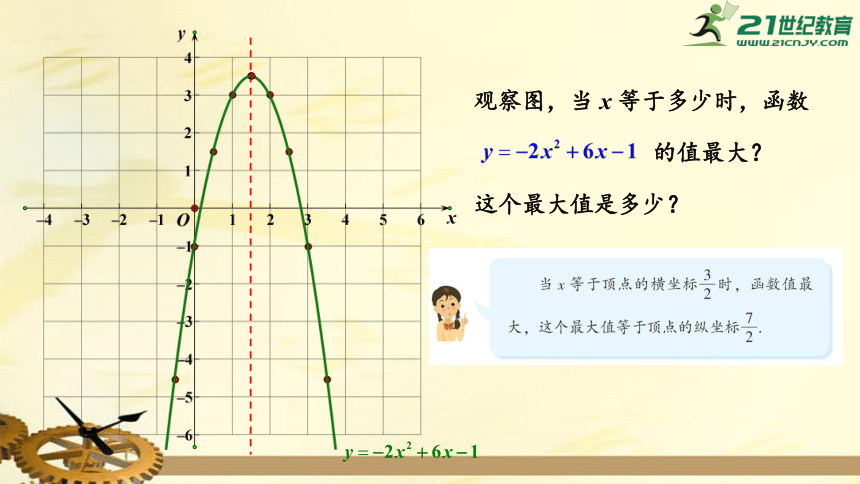
观察图,当
x
等于多少时,函数
的值最大?
这个最大值是多少?
一般地,
有下述结论:
二次函数
y
=
ax2
+
bx
+
c,
当
x
等于顶点的横坐标时,
达到最大值(a
<
0
)或最小值(a
>
0
),
这个最大(小)值等于顶点的纵坐标.
求二次函数
的最大值.
解
配方:
顶点坐标(2,1),于是当
x
=
2
时,y达到最大值
1.
【教材P17页】
根据下列关系你能发现二次函数
y=ax2+bx+c
的图象和性质吗?
y
=
ax2
+
bx
+
c
顶点坐标是
因此,当
时,函数达到最大值(a
<
0)或
最小值(a
>
0):
练习
1.
写出下列二次函数图象的对称轴、顶点坐标和开口方向,并画出它们的图象.
(1)
;
(2)
.
(1)对称轴
x
=
1,顶点坐标(1,-2),开口向上
(2)对称轴
x
=
2,顶点坐标(2,2),开口向下
【教材P18页】
练习
1.
写出下列二次函数图象的对称轴、顶点坐标和开口方向,并画出它们的图象.
(1)
;
(2)
.
【教材P18页】
2.
求下列二次函数图象的顶点坐标以及最大值或
最小值:
(1)
;
(2)
(1)
顶点坐标
最小值
(2)
顶点坐标(-3,4)
最小值
4
【教材P18页】
随堂练习
将二次函数
y
=
x2+2x-1
的图象沿
x
轴向右平移
2
个单位,
得到的函数表达式是(
)
A.y=(x+3)2-2
B.y=(x+3)2+2
C.y=(x-1)2+2
D.y=(x-1)2-2
D
2.
已知二次函数
y
=
a(x
-1)2+b
(a
≠
0)有最小值-1,
则
a
与
b
之间的大小关系是(
)
A.a<b
B.a
=
b
C.a>b
D.不能确定
C
3.
若一次函数
y
=
(a+1)
x+a
的图象过第一、三、四象限,
则二次函数
y=ax2-ax(
)
A.有最大值
B.有最大值-
C.有最小值
D.有最小值-
B
4.
已知抛物线
y=-x2+2x+2.
(1)通过配方求出它的对称轴、顶点坐标,并画出该抛物线;
(2)若该抛物线上两点
A
(x1
,
y1),
B(x2
,
y2)的横坐标满足
x1>x2>1,
试比较
y1
与
y2
的大小.
解:(1)配方:y
=-x2+2x+2
=-(x-1)2+3
对称轴是直线
x
=
-1,顶点坐标是(1,3)
(2)y1
<
y2
课堂小结
用配方法求二次函数
y
=
ax2
+
bx
+
c
的顶点坐标、对称轴;
y
=
ax2
+
bx
+
c
二次函数
y
=
ax2
+
bx
+
c
的图象特征与系数
a,b,c及b2-4ac
的符号之间的关系:
课堂小结
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
二次函数
y
=
ax?
+
bx
+
c(a≠0)的图象与性质
湘教版·九年级数学下册
上课课件
第1章
二次函数
学习目标
【知识与技能】
1.会用描点法画二次函数y=ax2+bx+c的图象.
2.会用配方法求抛物线y=ax2+bx+c的顶点坐标、开口方向、对称轴、y随x的增减性.
3.能通过配方求出二次函数y=ax2+bx+c(a≠0)的最大或最小值;能利用二次函数的性质求实际问题中的最大值或最小值.
【过程与方法】
1.经历探索二次函数y=ax2+bx+c(a≠0)的图象的作法和性质的过程,体会建立二次函数y=ax2+bx+c(a≠0)对称轴和顶点坐标公式的必要性.
2.在学习y=ax2+bx+c(a≠0)的性质的过程中,渗透转化(化归)的思想.
【情感态度】
进一步体会由特殊到一般的化归思想,形成积极参与数学活动的意识.
【教学重点】
①用配方法求y=ax2+bx+c的顶点坐标;②会用描点法画y=ax2+bx+c的图象并能说出图象的性质.
【教学难点】
能利用二次函数y=ax2+bx+c(a≠0)的对称轴和顶点坐标公式,解决一些问题,能通过对称性画出二次函数y=ax2+bx+c(a≠0)的图象.
探究新知
画出
的图象.
配方:
故对称轴是直线
,
顶点坐标是
.
列表:自变量
x
从顶点的横坐标
开始取值.
x
…
…
描点和连线:
画出图象在对称轴右边的部分.
利用对称性,
画出图象在对称轴左边的部分.这样就得到了
的图象.
观察图,当
x
等于多少时,函数
的值最大?
这个最大值是多少?
一般地,
有下述结论:
二次函数
y
=
ax2
+
bx
+
c,
当
x
等于顶点的横坐标时,
达到最大值(a
<
0
)或最小值(a
>
0
),
这个最大(小)值等于顶点的纵坐标.
求二次函数
的最大值.
解
配方:
顶点坐标(2,1),于是当
x
=
2
时,y达到最大值
1.
【教材P17页】
根据下列关系你能发现二次函数
y=ax2+bx+c
的图象和性质吗?
y
=
ax2
+
bx
+
c
顶点坐标是
因此,当
时,函数达到最大值(a
<
0)或
最小值(a
>
0):
练习
1.
写出下列二次函数图象的对称轴、顶点坐标和开口方向,并画出它们的图象.
(1)
;
(2)
.
(1)对称轴
x
=
1,顶点坐标(1,-2),开口向上
(2)对称轴
x
=
2,顶点坐标(2,2),开口向下
【教材P18页】
练习
1.
写出下列二次函数图象的对称轴、顶点坐标和开口方向,并画出它们的图象.
(1)
;
(2)
.
【教材P18页】
2.
求下列二次函数图象的顶点坐标以及最大值或
最小值:
(1)
;
(2)
(1)
顶点坐标
最小值
(2)
顶点坐标(-3,4)
最小值
4
【教材P18页】
随堂练习
将二次函数
y
=
x2+2x-1
的图象沿
x
轴向右平移
2
个单位,
得到的函数表达式是(
)
A.y=(x+3)2-2
B.y=(x+3)2+2
C.y=(x-1)2+2
D.y=(x-1)2-2
D
2.
已知二次函数
y
=
a(x
-1)2+b
(a
≠
0)有最小值-1,
则
a
与
b
之间的大小关系是(
)
A.a<b
B.a
=
b
C.a>b
D.不能确定
C
3.
若一次函数
y
=
(a+1)
x+a
的图象过第一、三、四象限,
则二次函数
y=ax2-ax(
)
A.有最大值
B.有最大值-
C.有最小值
D.有最小值-
B
4.
已知抛物线
y=-x2+2x+2.
(1)通过配方求出它的对称轴、顶点坐标,并画出该抛物线;
(2)若该抛物线上两点
A
(x1
,
y1),
B(x2
,
y2)的横坐标满足
x1>x2>1,
试比较
y1
与
y2
的大小.
解:(1)配方:y
=-x2+2x+2
=-(x-1)2+3
对称轴是直线
x
=
-1,顶点坐标是(1,3)
(2)y1
<
y2
课堂小结
用配方法求二次函数
y
=
ax2
+
bx
+
c
的顶点坐标、对称轴;
y
=
ax2
+
bx
+
c
二次函数
y
=
ax2
+
bx
+
c
的图象特征与系数
a,b,c及b2-4ac
的符号之间的关系:
课堂小结
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
