1.5 二次函数的应用(第2课时) 二次函数的应用(2) 课件(共20张PPT)
文档属性
| 名称 | 1.5 二次函数的应用(第2课时) 二次函数的应用(2) 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
二次函数的应用(2)
湘教版·九年级数学下册
上课课件
第1章
二次函数
学习目标
【知识与技能】
1.经历探索实际问题中两个变量的过程,使学生理解用抛物线知识解决最值问题的思路.
2.初步学会运用抛物线知识分析和解决实际问题.
【过程与方法】
经历优化问题的探究过程,认识数学与人类生活的密切联系及对人类历史发展的作用,发展我们运用数学知识解决实际问题的能力.
【情感态度】
体会数学与人类社会的密切联系,了解数学的价值,增加对数学的理解和学好数学的信心.
【教学重点】
能够分析和表示实际问题中变量之间的二次函数关系,并运用二次函数的知识求出实际问题的最值.
【教学难点】
二次函数最值在实际中生活中的应用,激发学生的学习兴趣.
知识回顾
总利润=总售价-________或总利润=每件商品利润×___________.
总成本
销售总量
一般地,
因为抛物线
y=ax2+bx+c
的顶点是最低(高)点,
所以当
x
=
________时,二次函数
y
=ax2+bx+c
有最小(大)值____________.
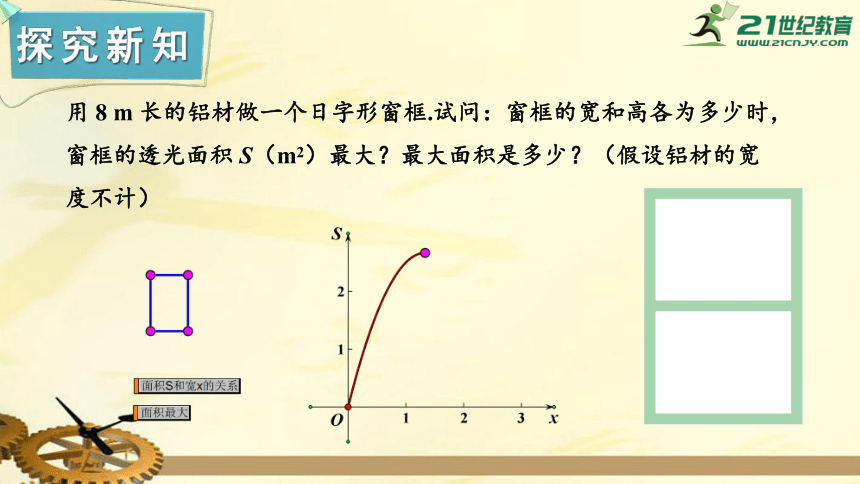
探究新知
用
8
m
长的铝材做一个日字形窗框.试问:窗框的宽和高各为多少时,窗框的透光面积
S(m2)最大?最大面积是多少?(假设铝材的宽度不计)
由于做窗框的铝材长度已确定,
而窗框的面积
S
随矩形一边长的变化而变化.
因此设窗框的宽为
x
m,
则窗框的高为
m,
其中
探究新知
用
8
m
长的铝材做一个日字形窗框.试问:窗框的宽和高各为多少时,窗框的透光面积
S(m2)最大?最大面积是多少?(假设铝材的宽度不计)
探究新知
用
8
m
长的铝材做一个日字形窗框.试问:窗框的宽和高各为多少时,窗框的透光面积
S(m2)最大?最大面积是多少?(假设铝材的宽度不计)
窗框的透光面积为
将上式进行配方,
当
x
=
时,
S
取最大值
.
探究新知
用
8
m
长的铝材做一个日字形窗框.试问:窗框的宽和高各为多少时,窗框的透光面积
S(m2)最大?最大面积是多少?(假设铝材的宽度不计)
这时高为
则当窗框的宽为
m,高为2m时,窗框的透光面积最大,最大透光面积为
m2.
某网络玩具店引进一批进价为
20
元/件的玩具,如果以单价
30
元销售,那么一个月内可售出
180
件.
根据销售经验,提高销售单价会导致销售量的下降,即销售单价每上涨
1
元,月销售量将相应减少10
件.
当销售单价为多少元时,该店能在一个月内获得最大利润?
进价/元
售价/元
数量/件
利润
现价
20
30
180
涨价
20
30
+
x
180-10x
某网络玩具店引进一批进价为
20
元/件的玩具,如果以单价
30
元销售,那么一个月内可售出
180
件.
根据销售经验,提高销售单价会导致销售量的下降,即销售单价每上涨
1
元,月销售量将相应减少10
件.
当销售单价为多少元时,该店能在一个月内获得最大利润?
解
设每件商品的销售单价上涨
x
元,
一个月内获取的商品总利润为
y
元.
每月减少的销售量为
10
x(件),
实际销售量为
180
-
10
x(件),
单件利润为(30
+
x
-
20
)元,
则
y
=
(10
+
x
)(180
-
10x
)
,
即
y
=
-
10x2
+
80x
+
1
800
(
0
≤
x
≤
18
)
.
将上式进行配方,y
=
-
10
(
x
-
4
)2
+
1
960.
当
x
=
4
时,即销售单价为
34
元时,
y
取最大值
1
960.
练习
小妍想将一根
72
cm
长的彩带剪成两段,
分别围成两个正方形,
则她要怎么剪才能让这两个正方形的面积和最小?
此时的面积和为多少?
解
设一段彩带长为
x
cm,则另一段彩带长为
72-x
cm
当
x
=
36
时,面积和有最小值为
162.
答:当剪的彩带长度都为36cm时两个正方形面积和最小,最小为162cm2.
随堂练习
1.
为搞好环保,某公司准备修建一个长方体的污水处理池,
若池底长方形的周长为100
m,则池底的最大面积是(
)
A.
600m2
B.
625m2
C.
650m2
D.
675m2
B
2.
便民商店经营一种商品,在销售过程中,发现一周利润
y(元)
与销售单价
x
(元)之间的关系满足
y
=-2(x-20)2+1558,
由于某种原因,价格需满足15
≤
x
≤
22,那么一周可获得最大利润是(
)
A.
20元
B.
1508元
C.
1550元
D.
1558元
D
3.
果农计划对果园加大种植密度,
据测算,
果园的总产量
y(个)与增种果树的棵数
x(棵)之间的函数表达式为
y
=
-5x2
+100x
+60
000
,
要使总产量在60
320
个以上,
需要增种果树的棵数范围是(
)
A.
4≤
x
≤
16
B.
x
≥
6
或
x
≤
16
C.
4<x<16
D.
x>6
或
x<16
C
4.某工艺厂设计了一款成本为10元/
件的产品,
并投放市场进行试销.
经过调查,发现每天的销售量
y(件)与销售单价
x(元)存在一次函数
关系
y
=
-
10x
+
700
.
(1)
销售单价定为多少时,该厂每天获取的利润最大?最大利润为多少?
(2)
若物价部门规定,该产品的最高销售单价不得超过35元,那么销售单价如何定位才能获取最大利润?
解
(1)每天获取的利润为
(-10x
+
700)(x
-
10)
=
-10(x
-
40)2
+
9000
,
x>0
当
x=40
时,最大利润为
9000
元
(2)y
=
-10(x
-
40)2
+
9000
,
当
0
<
x
<
40
时,利润随
x
的增大而增大,
因此,当
x=35
时,最大利润为
8750
元
课堂小结
一般步骤:
1.根据实际问题建立二次函数的关系式;
2.确定自变量取值范围;
3.求出实际问题的最值.
本节课主要是用二次函数理论知识解决最大面积问题和最大利润问题.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
二次函数的应用(2)
湘教版·九年级数学下册
上课课件
第1章
二次函数
学习目标
【知识与技能】
1.经历探索实际问题中两个变量的过程,使学生理解用抛物线知识解决最值问题的思路.
2.初步学会运用抛物线知识分析和解决实际问题.
【过程与方法】
经历优化问题的探究过程,认识数学与人类生活的密切联系及对人类历史发展的作用,发展我们运用数学知识解决实际问题的能力.
【情感态度】
体会数学与人类社会的密切联系,了解数学的价值,增加对数学的理解和学好数学的信心.
【教学重点】
能够分析和表示实际问题中变量之间的二次函数关系,并运用二次函数的知识求出实际问题的最值.
【教学难点】
二次函数最值在实际中生活中的应用,激发学生的学习兴趣.
知识回顾
总利润=总售价-________或总利润=每件商品利润×___________.
总成本
销售总量
一般地,
因为抛物线
y=ax2+bx+c
的顶点是最低(高)点,
所以当
x
=
________时,二次函数
y
=ax2+bx+c
有最小(大)值____________.
探究新知
用
8
m
长的铝材做一个日字形窗框.试问:窗框的宽和高各为多少时,窗框的透光面积
S(m2)最大?最大面积是多少?(假设铝材的宽度不计)
由于做窗框的铝材长度已确定,
而窗框的面积
S
随矩形一边长的变化而变化.
因此设窗框的宽为
x
m,
则窗框的高为
m,
其中
探究新知
用
8
m
长的铝材做一个日字形窗框.试问:窗框的宽和高各为多少时,窗框的透光面积
S(m2)最大?最大面积是多少?(假设铝材的宽度不计)
探究新知
用
8
m
长的铝材做一个日字形窗框.试问:窗框的宽和高各为多少时,窗框的透光面积
S(m2)最大?最大面积是多少?(假设铝材的宽度不计)
窗框的透光面积为
将上式进行配方,
当
x
=
时,
S
取最大值
.
探究新知
用
8
m
长的铝材做一个日字形窗框.试问:窗框的宽和高各为多少时,窗框的透光面积
S(m2)最大?最大面积是多少?(假设铝材的宽度不计)
这时高为
则当窗框的宽为
m,高为2m时,窗框的透光面积最大,最大透光面积为
m2.
某网络玩具店引进一批进价为
20
元/件的玩具,如果以单价
30
元销售,那么一个月内可售出
180
件.
根据销售经验,提高销售单价会导致销售量的下降,即销售单价每上涨
1
元,月销售量将相应减少10
件.
当销售单价为多少元时,该店能在一个月内获得最大利润?
进价/元
售价/元
数量/件
利润
现价
20
30
180
涨价
20
30
+
x
180-10x
某网络玩具店引进一批进价为
20
元/件的玩具,如果以单价
30
元销售,那么一个月内可售出
180
件.
根据销售经验,提高销售单价会导致销售量的下降,即销售单价每上涨
1
元,月销售量将相应减少10
件.
当销售单价为多少元时,该店能在一个月内获得最大利润?
解
设每件商品的销售单价上涨
x
元,
一个月内获取的商品总利润为
y
元.
每月减少的销售量为
10
x(件),
实际销售量为
180
-
10
x(件),
单件利润为(30
+
x
-
20
)元,
则
y
=
(10
+
x
)(180
-
10x
)
,
即
y
=
-
10x2
+
80x
+
1
800
(
0
≤
x
≤
18
)
.
将上式进行配方,y
=
-
10
(
x
-
4
)2
+
1
960.
当
x
=
4
时,即销售单价为
34
元时,
y
取最大值
1
960.
练习
小妍想将一根
72
cm
长的彩带剪成两段,
分别围成两个正方形,
则她要怎么剪才能让这两个正方形的面积和最小?
此时的面积和为多少?
解
设一段彩带长为
x
cm,则另一段彩带长为
72-x
cm
当
x
=
36
时,面积和有最小值为
162.
答:当剪的彩带长度都为36cm时两个正方形面积和最小,最小为162cm2.
随堂练习
1.
为搞好环保,某公司准备修建一个长方体的污水处理池,
若池底长方形的周长为100
m,则池底的最大面积是(
)
A.
600m2
B.
625m2
C.
650m2
D.
675m2
B
2.
便民商店经营一种商品,在销售过程中,发现一周利润
y(元)
与销售单价
x
(元)之间的关系满足
y
=-2(x-20)2+1558,
由于某种原因,价格需满足15
≤
x
≤
22,那么一周可获得最大利润是(
)
A.
20元
B.
1508元
C.
1550元
D.
1558元
D
3.
果农计划对果园加大种植密度,
据测算,
果园的总产量
y(个)与增种果树的棵数
x(棵)之间的函数表达式为
y
=
-5x2
+100x
+60
000
,
要使总产量在60
320
个以上,
需要增种果树的棵数范围是(
)
A.
4≤
x
≤
16
B.
x
≥
6
或
x
≤
16
C.
4<x<16
D.
x>6
或
x<16
C
4.某工艺厂设计了一款成本为10元/
件的产品,
并投放市场进行试销.
经过调查,发现每天的销售量
y(件)与销售单价
x(元)存在一次函数
关系
y
=
-
10x
+
700
.
(1)
销售单价定为多少时,该厂每天获取的利润最大?最大利润为多少?
(2)
若物价部门规定,该产品的最高销售单价不得超过35元,那么销售单价如何定位才能获取最大利润?
解
(1)每天获取的利润为
(-10x
+
700)(x
-
10)
=
-10(x
-
40)2
+
9000
,
x>0
当
x=40
时,最大利润为
9000
元
(2)y
=
-10(x
-
40)2
+
9000
,
当
0
<
x
<
40
时,利润随
x
的增大而增大,
因此,当
x=35
时,最大利润为
8750
元
课堂小结
一般步骤:
1.根据实际问题建立二次函数的关系式;
2.确定自变量取值范围;
3.求出实际问题的最值.
本节课主要是用二次函数理论知识解决最大面积问题和最大利润问题.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
