第1章 二次函数 小结与复习 课件(共24张PPT)
文档属性
| 名称 | 第1章 二次函数 小结与复习 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 00:00:00 | ||
图片预览


文档简介
(共24张PPT)
小结与复习
湘教版·九年级数学下册
上课课件
第1章
二次函数
学习目标
【知识与技能】
掌握本章重要知识,能灵活运用二次函数的图象与性质解决实际问题.
【过程与方法】
通过梳理本章知识,回顾解决问题中所涉及的数形结合思想,转化化归思想的过程,加深对本章知识的理解.
【情感态度】
在运用本章知识解决具体问题过程中,进一步体会数学与生活的密切联系,激发学习兴趣.
【教学重点】
回顾本章知识点,构建知识体系.
【教学难点】
利用二次函数的相关知识解决具体问题.
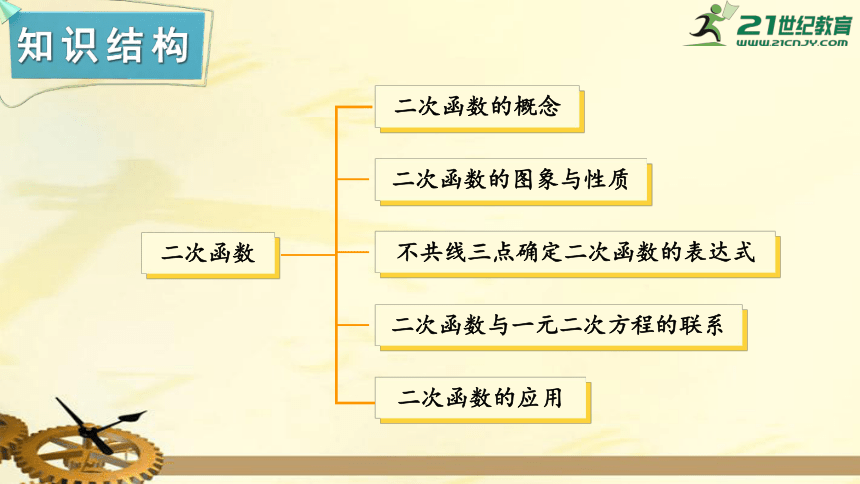
知识结构
二次函数
二次函数的概念
二次函数的图象与性质
不共线三点确定二次函数的表达式
二次函数与一元二次方程的联系
二次函数的应用
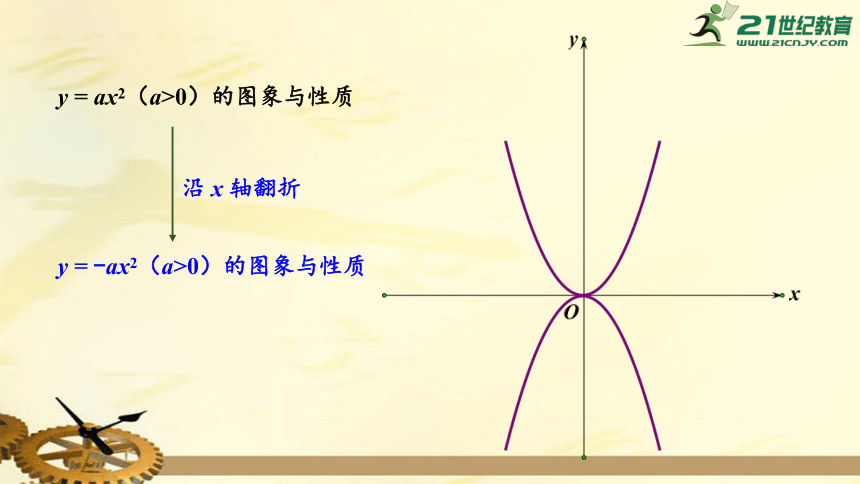
y
=
ax2(a>0)的图象与性质
沿
x
轴翻折
y
=
-ax2(a>0)的图象与性质
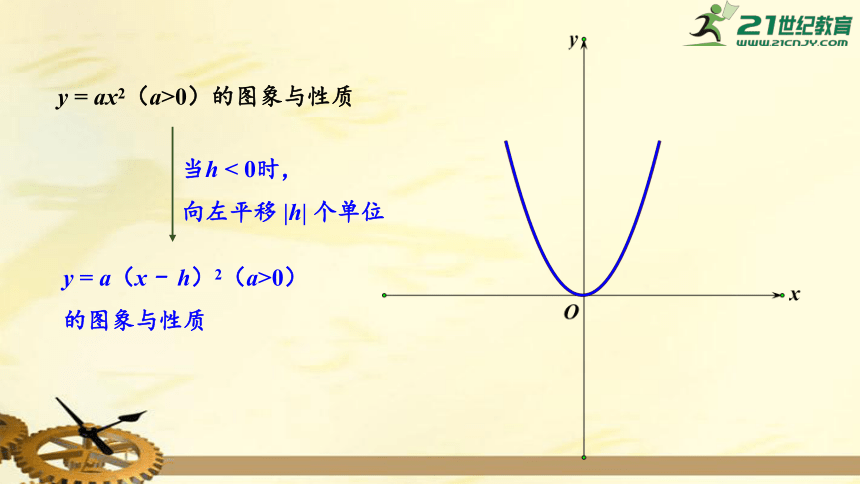
y
=
ax2(a>0)的图象与性质
当h
<
0时,
向左平移
|h|
个单位
y
=
a(x
-
h)2(a>0)的图象与性质
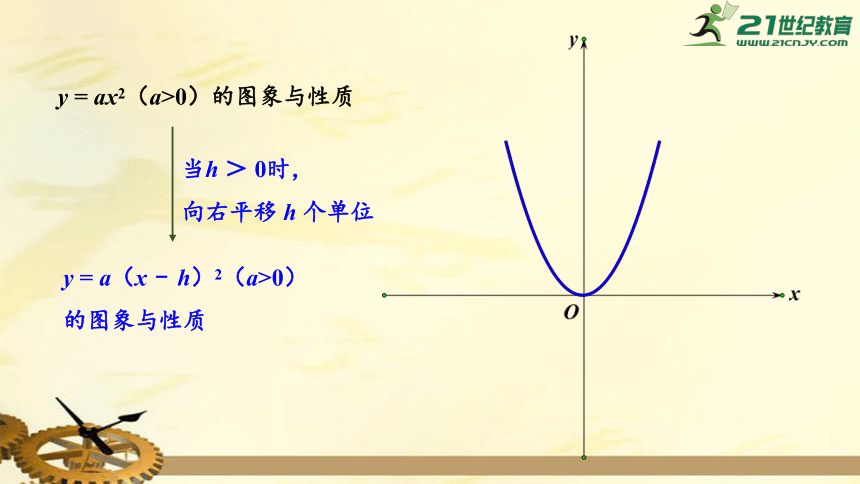
y
=
ax2(a>0)的图象与性质
当h
>
0时,
向右平移
h
个单位
y
=
a(x
-
h)2(a>0)的图象与性质
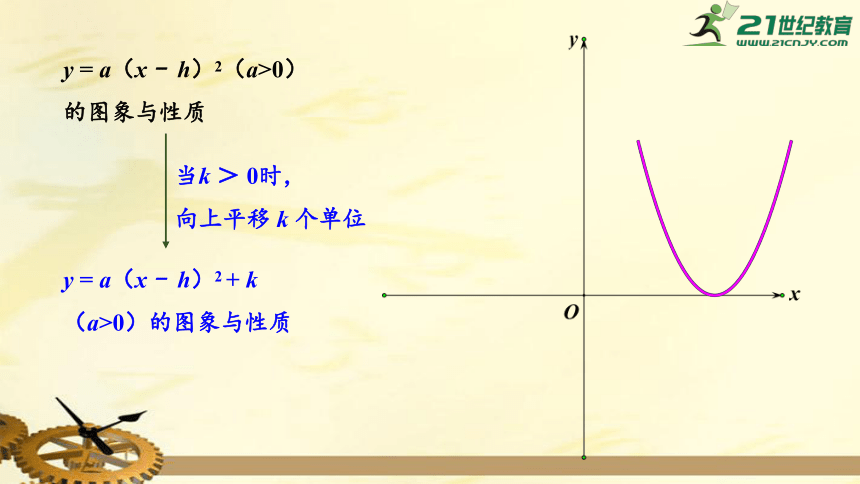
当k
>
0时,
向上平移
k
个单位
y
=
a(x
-
h)2(a>0)的图象与性质
y
=
a(x
-
h)2
+
k(a>0)的图象与性质
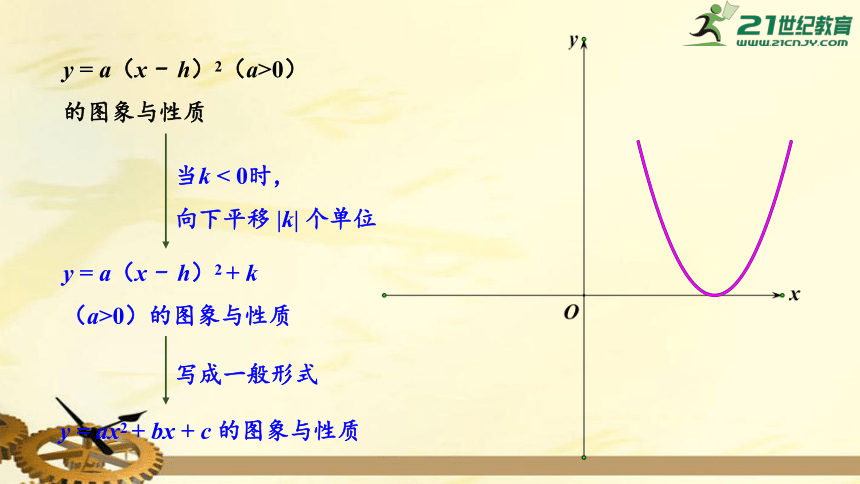
当k
<
0时,
向下平移
|k|
个单位
y
=
a(x
-
h)2(a>0)的图象与性质
y
=
a(x
-
h)2
+
k(a>0)的图象与性质
写成一般形式
y
=
ax2
+
bx
+
c
的图象与性质
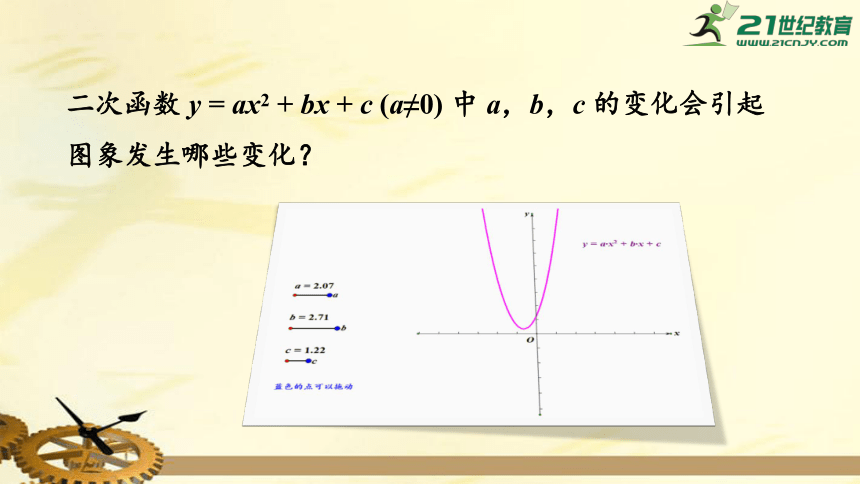
二次函数
y
=
ax2
+
bx
+
c
(a≠0)
中
a,b,c
的变化会引起图象发生哪些变化?
练习
1.如图,一张正方形纸板的边长为
4,将它剪去
4
个全等的直角三角形,设这
4
个直角三角形短直角边的长度为
x,四边形ABCD
的面积为
y,求
y
关于
x
的函数表达式.
y
=
2(x-2)2
+
8(0
<
x
≤
2)
【教材P37页】
2.
画出下列二次函数的图象,
并指出图象的对称轴、顶点坐标
和开口方向.
【教材P37页】
2.
画出下列二次函数的图象,
并指出图象的对称轴、顶点坐标
和开口方向.
【教材P37页】
2.
画出下列二次函数的图象,
并指出图象的对称轴、顶点坐标
和开口方向.
【教材P37页】
3.
填空:
(1)抛物线
y
=
3x2
先向左平移
2
个单位,得到抛物线_____________;
接着向上平移
1
个单位,得到抛物线__________________.
(2)抛物线
沿着
x
轴翻折并“复制”出来,得到抛物线_______;
接着向右平移
5
个单位,
得到抛物线_______________;
接着向下平移
2
个单位,
得到抛物线__________________
.
y
=
3(x+2)2
y
=
3(x+2)2+1
【教材P37页】
4.
已知二次函数的图象的顶点坐标为
,
且过点
.
求这个二次函数的表达式及它与
y
轴的交点坐标.
解
设二次函数的表达式为
将点
代入,得
所以,二次函数表达式
与
y
轴交点
【教材P37页】
5.
用配方法求下列二次函数的最大值或最小值.
解
最大值
最小值
-3
【教材P37页】
6.
已知二次函数的图象与
x
轴交于点(2,0)
,
(-1,0),
与
y
轴
交于点(0,-1).
求这个二次函数的表达式及顶点坐标.
解
设二次函数表达式为
将点(0,-1)代入,得
顶点坐标
【教材P37页】
7.
用图象法求一元二次方程
x2+
4x
-
3
=
0
的根的
近似值(精确到
0.1).
y
=
x2+
4x
-
3
x1
≈
-4.7
x2
≈
0.7
【教材P37页】
8.
将一个小球以
20m/s
的初速度从地面垂直抛向空中,经过时间
t
(s),小球的高度
h(m)为
h
=
20t
-
5t2
.
(1)经过多长时间,小球达到最高点?此时小球离地面多高?
(2)经过多长时间,小球落到地上?
【教材P38页】
8.
将一个小球以
20m/s
的初速度从地面垂直抛向空中,经过时间
t
(s),小球的高度
h(m)为
h
=
20t
-
5t2
.
(1)经过多长时间,小球达到最高点?此时小球离地面多高?
(2)经过多长时间,小球落到地上?
解
h
=
20t
-
5t2
=
-5(t-2)2
+
20
当
t
=
2
时,小球达到最高点,离地面
20
m,
当
t
=
4时,小球落到地上.
【教材P38页】
课堂小结
1.
说一说本节课的收获。
2.
你还存在哪些疑惑?
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
小结与复习
湘教版·九年级数学下册
上课课件
第1章
二次函数
学习目标
【知识与技能】
掌握本章重要知识,能灵活运用二次函数的图象与性质解决实际问题.
【过程与方法】
通过梳理本章知识,回顾解决问题中所涉及的数形结合思想,转化化归思想的过程,加深对本章知识的理解.
【情感态度】
在运用本章知识解决具体问题过程中,进一步体会数学与生活的密切联系,激发学习兴趣.
【教学重点】
回顾本章知识点,构建知识体系.
【教学难点】
利用二次函数的相关知识解决具体问题.
知识结构
二次函数
二次函数的概念
二次函数的图象与性质
不共线三点确定二次函数的表达式
二次函数与一元二次方程的联系
二次函数的应用
y
=
ax2(a>0)的图象与性质
沿
x
轴翻折
y
=
-ax2(a>0)的图象与性质
y
=
ax2(a>0)的图象与性质
当h
<
0时,
向左平移
|h|
个单位
y
=
a(x
-
h)2(a>0)的图象与性质
y
=
ax2(a>0)的图象与性质
当h
>
0时,
向右平移
h
个单位
y
=
a(x
-
h)2(a>0)的图象与性质
当k
>
0时,
向上平移
k
个单位
y
=
a(x
-
h)2(a>0)的图象与性质
y
=
a(x
-
h)2
+
k(a>0)的图象与性质
当k
<
0时,
向下平移
|k|
个单位
y
=
a(x
-
h)2(a>0)的图象与性质
y
=
a(x
-
h)2
+
k(a>0)的图象与性质
写成一般形式
y
=
ax2
+
bx
+
c
的图象与性质
二次函数
y
=
ax2
+
bx
+
c
(a≠0)
中
a,b,c
的变化会引起图象发生哪些变化?
练习
1.如图,一张正方形纸板的边长为
4,将它剪去
4
个全等的直角三角形,设这
4
个直角三角形短直角边的长度为
x,四边形ABCD
的面积为
y,求
y
关于
x
的函数表达式.
y
=
2(x-2)2
+
8(0
<
x
≤
2)
【教材P37页】
2.
画出下列二次函数的图象,
并指出图象的对称轴、顶点坐标
和开口方向.
【教材P37页】
2.
画出下列二次函数的图象,
并指出图象的对称轴、顶点坐标
和开口方向.
【教材P37页】
2.
画出下列二次函数的图象,
并指出图象的对称轴、顶点坐标
和开口方向.
【教材P37页】
3.
填空:
(1)抛物线
y
=
3x2
先向左平移
2
个单位,得到抛物线_____________;
接着向上平移
1
个单位,得到抛物线__________________.
(2)抛物线
沿着
x
轴翻折并“复制”出来,得到抛物线_______;
接着向右平移
5
个单位,
得到抛物线_______________;
接着向下平移
2
个单位,
得到抛物线__________________
.
y
=
3(x+2)2
y
=
3(x+2)2+1
【教材P37页】
4.
已知二次函数的图象的顶点坐标为
,
且过点
.
求这个二次函数的表达式及它与
y
轴的交点坐标.
解
设二次函数的表达式为
将点
代入,得
所以,二次函数表达式
与
y
轴交点
【教材P37页】
5.
用配方法求下列二次函数的最大值或最小值.
解
最大值
最小值
-3
【教材P37页】
6.
已知二次函数的图象与
x
轴交于点(2,0)
,
(-1,0),
与
y
轴
交于点(0,-1).
求这个二次函数的表达式及顶点坐标.
解
设二次函数表达式为
将点(0,-1)代入,得
顶点坐标
【教材P37页】
7.
用图象法求一元二次方程
x2+
4x
-
3
=
0
的根的
近似值(精确到
0.1).
y
=
x2+
4x
-
3
x1
≈
-4.7
x2
≈
0.7
【教材P37页】
8.
将一个小球以
20m/s
的初速度从地面垂直抛向空中,经过时间
t
(s),小球的高度
h(m)为
h
=
20t
-
5t2
.
(1)经过多长时间,小球达到最高点?此时小球离地面多高?
(2)经过多长时间,小球落到地上?
【教材P38页】
8.
将一个小球以
20m/s
的初速度从地面垂直抛向空中,经过时间
t
(s),小球的高度
h(m)为
h
=
20t
-
5t2
.
(1)经过多长时间,小球达到最高点?此时小球离地面多高?
(2)经过多长时间,小球落到地上?
解
h
=
20t
-
5t2
=
-5(t-2)2
+
20
当
t
=
2
时,小球达到最高点,离地面
20
m,
当
t
=
4时,小球落到地上.
【教材P38页】
课堂小结
1.
说一说本节课的收获。
2.
你还存在哪些疑惑?
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
