人教版九年级下册28.1 锐角三角函数(第2课时)课件(21张PPT)
文档属性
| 名称 | 人教版九年级下册28.1 锐角三角函数(第2课时)课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 06:58:09 | ||
图片预览







文档简介
(共21张PPT)
第二十八章 锐角三角函数
28.1 锐角三角函数
第二课时
一、情景导入
如图,在
Rt△ABC
中,∠C=90?,当∠A
确定时,∠A
的对边与斜边的比就随之确定.
此时,其他边之间的比是否也确定了呢?
A
B
C
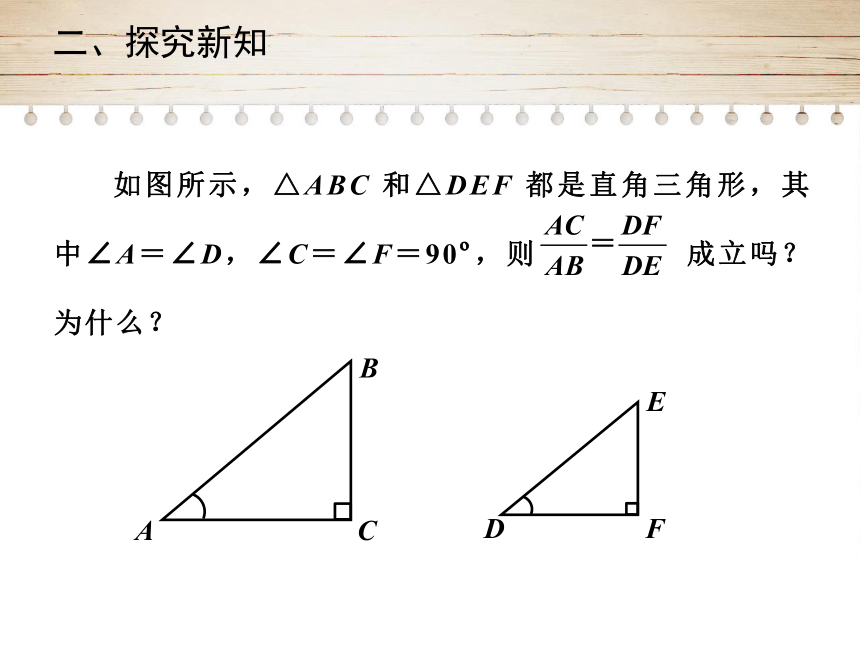
二、探究新知
如图所示,△ABC
和△DEF
都是直角三角形,其中∠A=∠D,∠C=∠F=90?,则
成立吗?为什么?
A
B
C
D
E
F
二、探究新知
证明:∵ ∠A=∠D,∠C=∠F=90?,
∴ Rt△ABC∽Rt△DEF.
∴
即
二、探究新知
如图所示,△ABC
和△DEF
都是直角三角形,其中∠A=∠D,∠C=∠F=90?,则
成立吗?为什么?
A
B
C
D
E
F
二、探究新知
证明:∵ ∠A=∠D
,∠C=∠F=90?,
∴
Rt△ABC
∽
Rt△DEF.
∴
∴
二、探究新知
如图,当∠A
确定时,∠A
的邻边与斜边的比,∠A
的对边与邻边的比都是确定的.
我们把∠A
的邻边与斜边的比叫做∠A
的余弦,记作
cos
A,即
把∠A
的对边与邻边的比叫做
∠A
的正切,记作
tan
A,
即
A
B
C
二、探究新知
注意:
(1)若角是用一个大写字母或一个小写希腊字母表示的,则
sin
A
,cos
A,tan
A
的写法中可省去角的符号“∠”.
(2)sin
A,cos
A,tan
A
是一个比值,是两条线段长度的比,是没有单位的.
(3)sin
A,
cos
A,tan
A
分别是一个整体符号,如
cos
A
不表示“cos”乘以“A”.
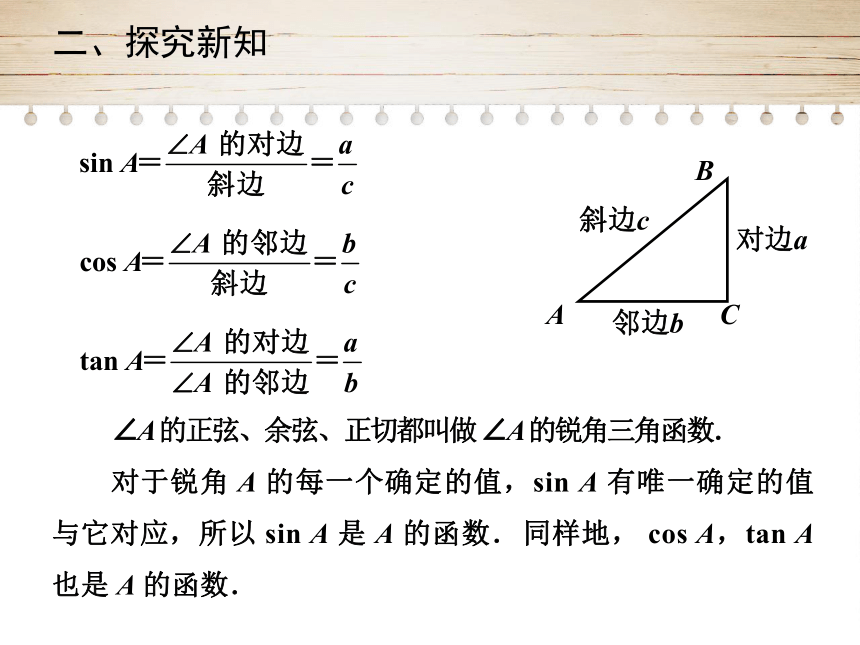
二、探究新知
∠A
的正弦、余弦、正切都叫做
∠A
的锐角三角函数.
对于锐角
A
的每一个确定的值,sin
A
有唯一确定的值与它对应,所以
sin
A
是
A
的函数.同样地,
cos
A,tan
A
也是
A
的函数.
A
B
C
斜边c
对边a
邻边b
二、探究新知
例
1 如图,在
Rt△ABC
中,∠C=90?,AB=10,BC=6,求
sin
A,cos
A,tan
A
的值.
解:由勾股定理得
因此
A
B
C
10
6
二、探究新知
1.在
Rt△ABC
中,∠C=90?,AC=12,AB=13.
sin
A=______,cos
A=______,tan
A=______,
sin
B=______,cos
B=______,tan
B=______.
A
B
C
12
13
二、探究新知
2.在
Rt△ABC
中,∠C=90?,AC=2,BC=3.
sin
A=
_______,cos
A=_______,tan
A=_____,
sin
B=
_______,cos
B=_______,tan
B=_____.
A
C
B
2
3
二、探究新知
结论:一个锐角的正弦等于它余角的余弦,或一个锐角的余弦等于它余角的正弦,一个锐角的正切和它余角的正切互为倒数.
sin
A=cos(90?-A)
cos
A=sin(90?-A)
tan
A·tan(90?-A)=1
二、探究新知
例
2 如图,在
Rt△ABC
中,∠C=90?,BC=6,sin
A=
,求
cos
A、tan
B
的值.
解:∵
又
∴
A
B
C
6
三、课堂小结
余弦函数和
正切函数
余弦:在直角三角形中,锐角
A
的邻边与斜边的比叫做角
A
的余弦.
正切:在直角三角形中,锐角
A
的对边与邻边的比叫做角
A
的正切.
性质:∠A
的大小确定的情况下,cos
A,tan
A为定值,与三角形的大小无关.
四、课堂训练
1.如图,在边长为
1
的小正方形组成的网格中,△ABC
的三个顶点均在格点上,则
cos
A=( ).
C
四、课堂训练
2.如图,在
Rt△ABC
中,斜边
AB
的长为
m,∠A=35?,则直角边
BC
的长是( ).
A
B
C
A
四、课堂训练
3.已知∠A,∠B
为锐角,
(1)若∠A=∠B,则
cos
A______cos
B;
(2)若
tan
A=tan
B,则∠A______∠B.
(3)若
tan
A·tan
B=1,则
∠A
与
∠B
的关系为:
_____________.
4.tan
30?=______
,tan
60?=
______.
=
=
∠A
+∠B=90?
四、课堂训练
5.如图,直径为
5
的
⊙A
经过点
C(0,3)和点
O(0,0),B是
y
轴右侧
⊙A
优弧上一点,则
∠OBC
的余弦值为
_____.
方法总结:在圆中求锐角三角
函数值时,常通过直径构造直角三
角形,并利用同弧或等弧所对的圆
周角相等,将角转化到直角三角形
中,进而求出三角函数值.
四、课堂训练
6.如图,在
Rt△ABC
中,∠C=90?,cos
A=
,求
sin
A,tan
A
的值.
解:
设
AC=15k,则
AB=17k.
∴
∴
方法总结:设而不求是设参数法求锐角三角函数值的常用方法.
A
B
C
五、作业
教科书习题
28.1
第
1,2
题.
第二十八章 锐角三角函数
28.1 锐角三角函数
第二课时
一、情景导入
如图,在
Rt△ABC
中,∠C=90?,当∠A
确定时,∠A
的对边与斜边的比就随之确定.
此时,其他边之间的比是否也确定了呢?
A
B
C
二、探究新知
如图所示,△ABC
和△DEF
都是直角三角形,其中∠A=∠D,∠C=∠F=90?,则
成立吗?为什么?
A
B
C
D
E
F
二、探究新知
证明:∵ ∠A=∠D,∠C=∠F=90?,
∴ Rt△ABC∽Rt△DEF.
∴
即
二、探究新知
如图所示,△ABC
和△DEF
都是直角三角形,其中∠A=∠D,∠C=∠F=90?,则
成立吗?为什么?
A
B
C
D
E
F
二、探究新知
证明:∵ ∠A=∠D
,∠C=∠F=90?,
∴
Rt△ABC
∽
Rt△DEF.
∴
∴
二、探究新知
如图,当∠A
确定时,∠A
的邻边与斜边的比,∠A
的对边与邻边的比都是确定的.
我们把∠A
的邻边与斜边的比叫做∠A
的余弦,记作
cos
A,即
把∠A
的对边与邻边的比叫做
∠A
的正切,记作
tan
A,
即
A
B
C
二、探究新知
注意:
(1)若角是用一个大写字母或一个小写希腊字母表示的,则
sin
A
,cos
A,tan
A
的写法中可省去角的符号“∠”.
(2)sin
A,cos
A,tan
A
是一个比值,是两条线段长度的比,是没有单位的.
(3)sin
A,
cos
A,tan
A
分别是一个整体符号,如
cos
A
不表示“cos”乘以“A”.
二、探究新知
∠A
的正弦、余弦、正切都叫做
∠A
的锐角三角函数.
对于锐角
A
的每一个确定的值,sin
A
有唯一确定的值与它对应,所以
sin
A
是
A
的函数.同样地,
cos
A,tan
A
也是
A
的函数.
A
B
C
斜边c
对边a
邻边b
二、探究新知
例
1 如图,在
Rt△ABC
中,∠C=90?,AB=10,BC=6,求
sin
A,cos
A,tan
A
的值.
解:由勾股定理得
因此
A
B
C
10
6
二、探究新知
1.在
Rt△ABC
中,∠C=90?,AC=12,AB=13.
sin
A=______,cos
A=______,tan
A=______,
sin
B=______,cos
B=______,tan
B=______.
A
B
C
12
13
二、探究新知
2.在
Rt△ABC
中,∠C=90?,AC=2,BC=3.
sin
A=
_______,cos
A=_______,tan
A=_____,
sin
B=
_______,cos
B=_______,tan
B=_____.
A
C
B
2
3
二、探究新知
结论:一个锐角的正弦等于它余角的余弦,或一个锐角的余弦等于它余角的正弦,一个锐角的正切和它余角的正切互为倒数.
sin
A=cos(90?-A)
cos
A=sin(90?-A)
tan
A·tan(90?-A)=1
二、探究新知
例
2 如图,在
Rt△ABC
中,∠C=90?,BC=6,sin
A=
,求
cos
A、tan
B
的值.
解:∵
又
∴
A
B
C
6
三、课堂小结
余弦函数和
正切函数
余弦:在直角三角形中,锐角
A
的邻边与斜边的比叫做角
A
的余弦.
正切:在直角三角形中,锐角
A
的对边与邻边的比叫做角
A
的正切.
性质:∠A
的大小确定的情况下,cos
A,tan
A为定值,与三角形的大小无关.
四、课堂训练
1.如图,在边长为
1
的小正方形组成的网格中,△ABC
的三个顶点均在格点上,则
cos
A=( ).
C
四、课堂训练
2.如图,在
Rt△ABC
中,斜边
AB
的长为
m,∠A=35?,则直角边
BC
的长是( ).
A
B
C
A
四、课堂训练
3.已知∠A,∠B
为锐角,
(1)若∠A=∠B,则
cos
A______cos
B;
(2)若
tan
A=tan
B,则∠A______∠B.
(3)若
tan
A·tan
B=1,则
∠A
与
∠B
的关系为:
_____________.
4.tan
30?=______
,tan
60?=
______.
=
=
∠A
+∠B=90?
四、课堂训练
5.如图,直径为
5
的
⊙A
经过点
C(0,3)和点
O(0,0),B是
y
轴右侧
⊙A
优弧上一点,则
∠OBC
的余弦值为
_____.
方法总结:在圆中求锐角三角
函数值时,常通过直径构造直角三
角形,并利用同弧或等弧所对的圆
周角相等,将角转化到直角三角形
中,进而求出三角函数值.
四、课堂训练
6.如图,在
Rt△ABC
中,∠C=90?,cos
A=
,求
sin
A,tan
A
的值.
解:
设
AC=15k,则
AB=17k.
∴
∴
方法总结:设而不求是设参数法求锐角三角函数值的常用方法.
A
B
C
五、作业
教科书习题
28.1
第
1,2
题.
