人教版九年级下册28.1 锐角三角函数(第3课时)课件(18张PPT)
文档属性
| 名称 | 人教版九年级下册28.1 锐角三角函数(第3课时)课件(18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 06:54:50 | ||
图片预览



文档简介
(共18张PPT)
第二十八章 锐角三角函数
28.1 锐角三角函数
第三课时
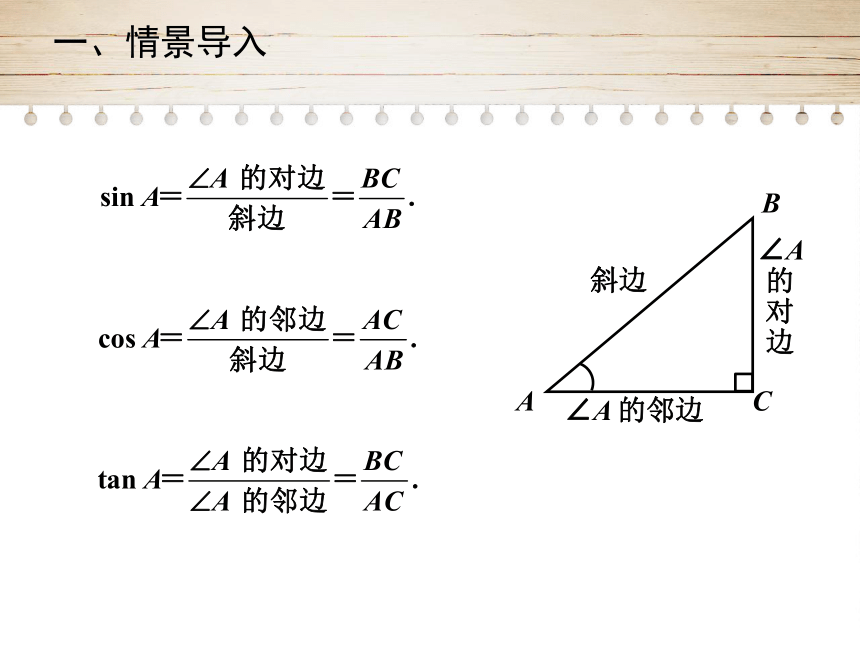
一、情景导入
为了测量一棵大树的高度,准备了如下测量工具:
①
含
30?和
60?两个锐角的三角尺;
②
皮尺.请你设计一个测量方案,测出一棵大树的高度.你会吗?
一、情景导入
A
B
C
∠A
的邻边
∠A
的
对
边
斜边
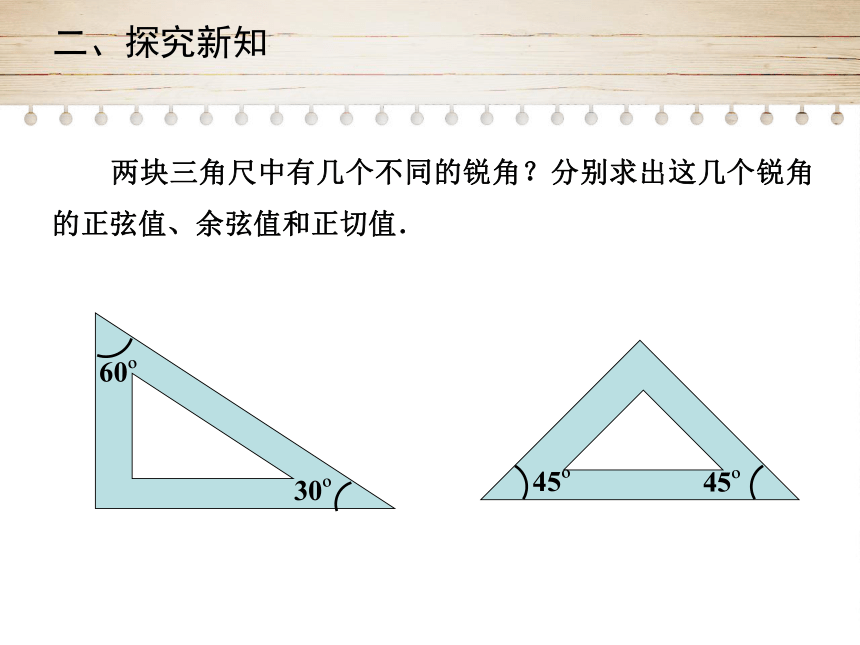
二、探究新知
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
30?
60?
45?
45?
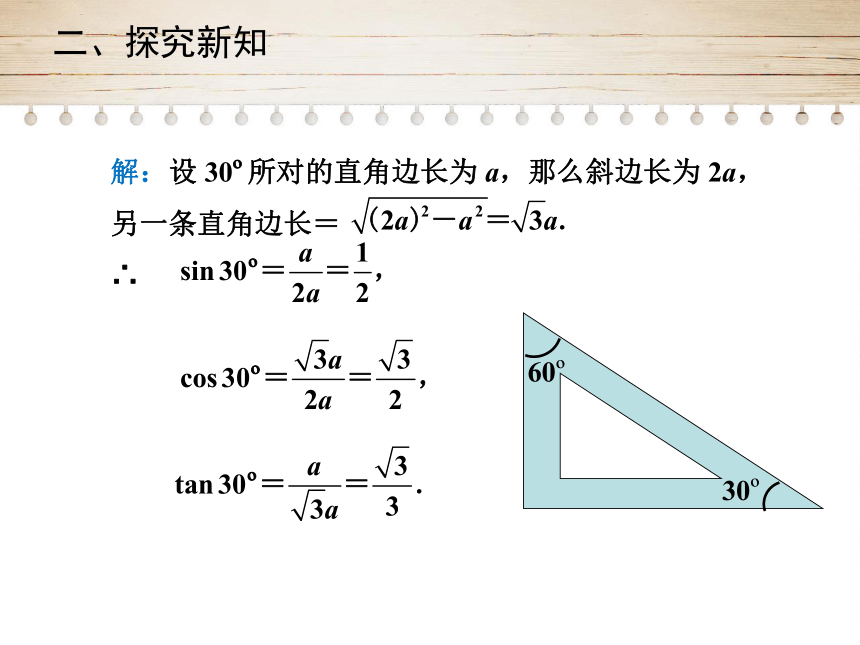
二、探究新知
解:设
30?所对的直角边长为
a,那么斜边长为
2a,
另一条直角边长=
∴
30?
60?
二、探究新知
∴
30?
60?
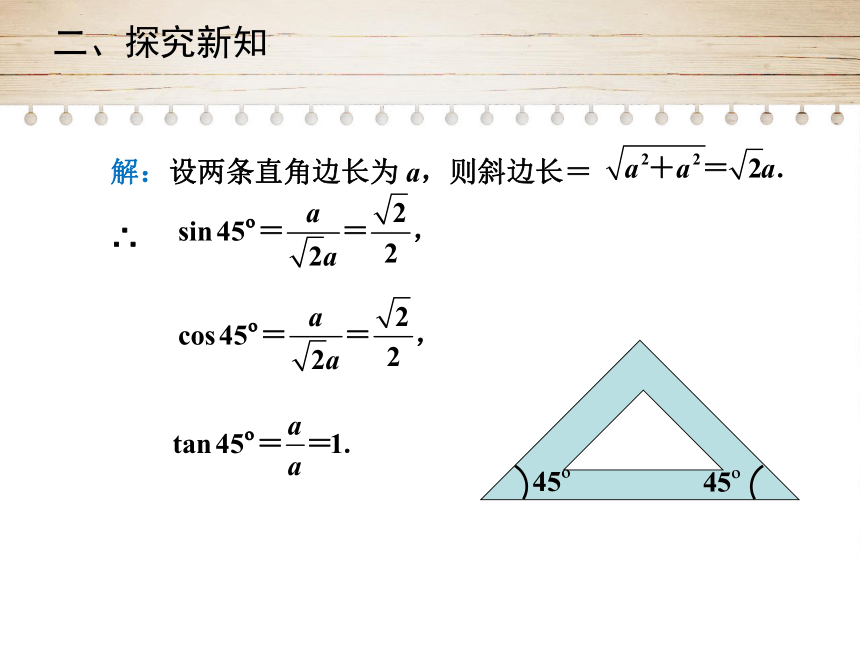
二、探究新知
解:设两条直角边长为
a,则斜边长=
∴
45?
45?
二、探究新知
归纳:
30?、45?、60?角的正弦值、余弦值和正切值如下表:
锐角
A
锐角
三角
函数
30?
45?
60?
sin
A
cos
A
tan
A
二、探究新知
例
1 求下列各式的值:
(1)cos2
60?+sin2
60?;
(2)
解:(1)cos2
60?+sin2
60
(2)
方法总结:有关特殊角的三角函数值的计算,先写出三角函数值,将运算转化为实数的混合运算,然后根据实数的运算法则计算.
二、探究新知
计算:
(1)sin
30?+cos
45?;
(2)sin2
30?+cos2
30?-tan
45?.
解:(1)原式=
(2)原式=
二、探究新知
例
2 (1)如图,在
Rt△ABC
中,∠C=90?,AB=
,
BC=
,求
∠A
的度数;
解:在图中,
∵
∴
∠A=45?.
A
B
C
二、探究新知
(2)如图,AO
是圆锥的高,OB
是底面半径,AO=
OB,求
α
的度数.
解:
在图中,
∵ tan
α=
∴
α
=
60?.
方法总结:根据一个锐角的特殊三角函数值,也可以求出角的度数.
A
B
O
二、探究新知
例
3 如图,在△ABC
中,∠A=30?,
求
AB.
解:过点
C
作
CD⊥AB
于点
D,∠A=30?,
A
B
C
D
二、探究新知
方法总结:锐角三角函数是在直角三角形中定义的,当此锐角所在的三角形不是直角三角形时,必须通过作辅助线构造出直角三角形求解
.
A
B
C
D
三、课堂小结
30?、45?、60?
角的三角函数值
通过三角函数值求角度
特殊角的
三角函数值
四、课堂训练
1.
tan(α+20?)=1,锐角
α
的度数应是( ).
A.40?
B.30?
C.20?
D.10?
2.已知
sin
A=
,则下列正确的是( ).
A.cos
A=
B.cos
A=
C.tan
A=
1
D.tan
A=
D
B
四、课堂训练
3.求下列各式的值:
(1)
1-2
sin
30?cos
30?;
(2)
3tan
30?-tan
45?+2sin
60?
;
(3)
答案:(1)
;(2)
;(3)
2.
五、作业
教科书习题
28.
1第
3
题.
第二十八章 锐角三角函数
28.1 锐角三角函数
第三课时
一、情景导入
为了测量一棵大树的高度,准备了如下测量工具:
①
含
30?和
60?两个锐角的三角尺;
②
皮尺.请你设计一个测量方案,测出一棵大树的高度.你会吗?
一、情景导入
A
B
C
∠A
的邻边
∠A
的
对
边
斜边
二、探究新知
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
30?
60?
45?
45?
二、探究新知
解:设
30?所对的直角边长为
a,那么斜边长为
2a,
另一条直角边长=
∴
30?
60?
二、探究新知
∴
30?
60?
二、探究新知
解:设两条直角边长为
a,则斜边长=
∴
45?
45?
二、探究新知
归纳:
30?、45?、60?角的正弦值、余弦值和正切值如下表:
锐角
A
锐角
三角
函数
30?
45?
60?
sin
A
cos
A
tan
A
二、探究新知
例
1 求下列各式的值:
(1)cos2
60?+sin2
60?;
(2)
解:(1)cos2
60?+sin2
60
(2)
方法总结:有关特殊角的三角函数值的计算,先写出三角函数值,将运算转化为实数的混合运算,然后根据实数的运算法则计算.
二、探究新知
计算:
(1)sin
30?+cos
45?;
(2)sin2
30?+cos2
30?-tan
45?.
解:(1)原式=
(2)原式=
二、探究新知
例
2 (1)如图,在
Rt△ABC
中,∠C=90?,AB=
,
BC=
,求
∠A
的度数;
解:在图中,
∵
∴
∠A=45?.
A
B
C
二、探究新知
(2)如图,AO
是圆锥的高,OB
是底面半径,AO=
OB,求
α
的度数.
解:
在图中,
∵ tan
α=
∴
α
=
60?.
方法总结:根据一个锐角的特殊三角函数值,也可以求出角的度数.
A
B
O
二、探究新知
例
3 如图,在△ABC
中,∠A=30?,
求
AB.
解:过点
C
作
CD⊥AB
于点
D,∠A=30?,
A
B
C
D
二、探究新知
方法总结:锐角三角函数是在直角三角形中定义的,当此锐角所在的三角形不是直角三角形时,必须通过作辅助线构造出直角三角形求解
.
A
B
C
D
三、课堂小结
30?、45?、60?
角的三角函数值
通过三角函数值求角度
特殊角的
三角函数值
四、课堂训练
1.
tan(α+20?)=1,锐角
α
的度数应是( ).
A.40?
B.30?
C.20?
D.10?
2.已知
sin
A=
,则下列正确的是( ).
A.cos
A=
B.cos
A=
C.tan
A=
1
D.tan
A=
D
B
四、课堂训练
3.求下列各式的值:
(1)
1-2
sin
30?cos
30?;
(2)
3tan
30?-tan
45?+2sin
60?
;
(3)
答案:(1)
;(2)
;(3)
2.
五、作业
教科书习题
28.
1第
3
题.
