人教版九年级下册28.2.2解直角三角形应用举例(第1课时)课件(25张PPT)
文档属性
| 名称 | 人教版九年级下册28.2.2解直角三角形应用举例(第1课时)课件(25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 07:03:18 | ||
图片预览





文档简介
(共25张PPT)
第二十八章 锐角三角函数
28.2 解直角三角形及其应用
28.2.2 应用举例
第一课时
一、情景导入
高跟鞋深受很多女性的喜爱,但有时候,如果鞋跟太高,不仅腿脚容易疲劳,还有可能会“闹笑话”.
专家认为当人的脚掌长为
15
cm,鞋跟约在
3
cm
左右高度感觉最舒适,由此你能算出高跟鞋的鞋底与地面的夹角吗?生活中解直角三角形的应用非常广泛.
二、探究新知
例
1 2012
年
6
月
18
日,
“神州”九号载人航天飞船与“天宫”一号目标飞行器成功实现交会对接.“神州”九号与“天宫”一号的组合体在离地球表面
343
km
的圆形轨道上运行.如图,当组合体运行到离地球表面
P
点的正上方时,从中能直接看到的地球表面最远的点在什么位置?最远点与
P
点的距离是多少(地球半径约为
6400
km,
π
取
3.142
,
结果取整数)?
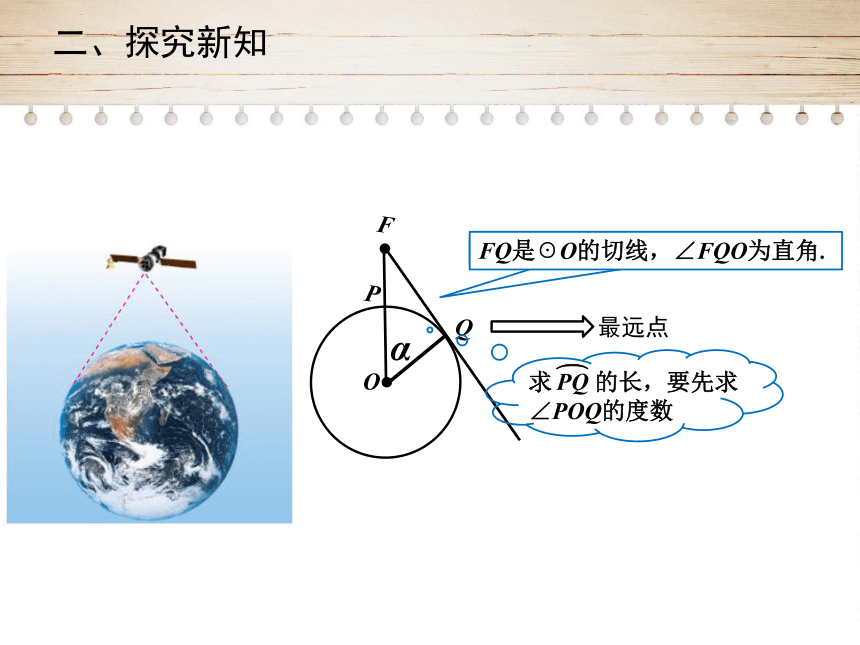
二、探究新知
FQ是☉O的切线,∠FQO为直角.
最远点
·
P
Q
O
α
F
求
的长,要先求∠POQ的度数
二、探究新知
解:连接
OQ,设∠POQ=α,
∵ FQ
是
☉O
的切线,
∴ △FOQ
是直角三角形.
∴
的长为
·
P
Q
O
二、探究新知
当飞船在
P
点正上方时,从飞船观测地球时的最远点距离
P
点约
2
051
km.
二、探究新知
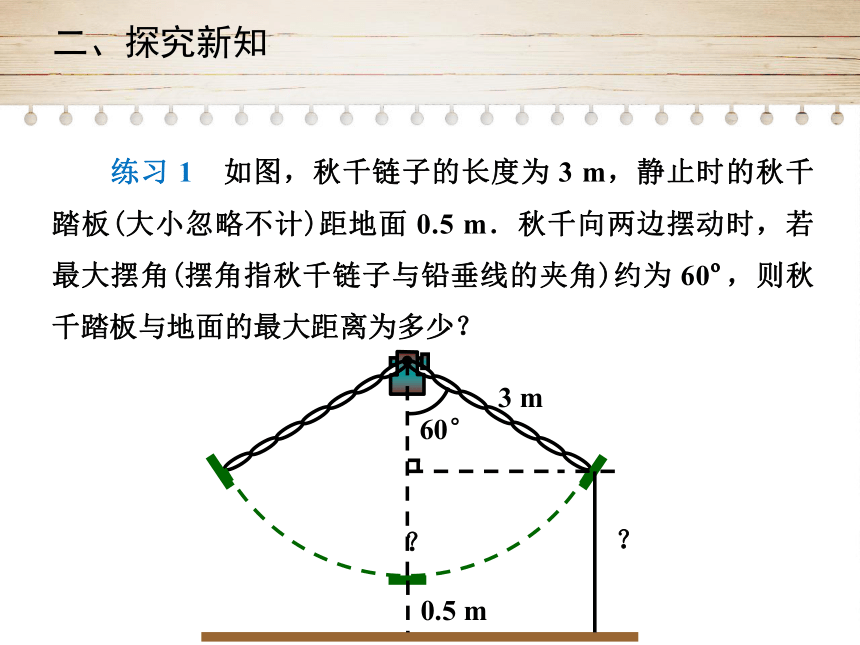
练习
1 如图,秋千链子的长度为
3
m,静止时的秋千踏板(大小忽略不计)距地面
0.5
m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为
60?,则秋千踏板与地面的最大距离为多少?
0.5
m
3
m
60°
?
?
二、探究新知
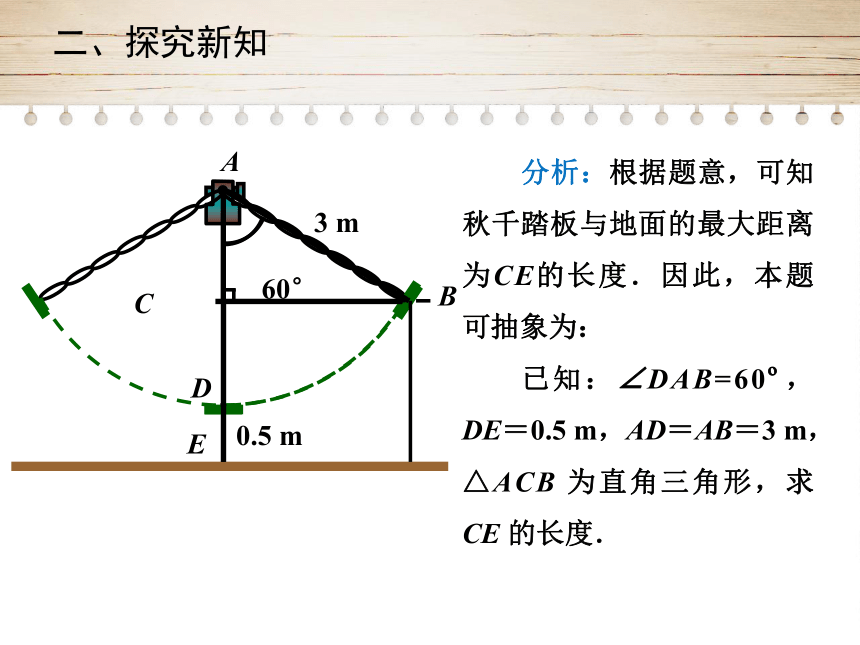
分析:根据题意,可知秋千踏板与地面的最大距离为CE的长度.因此,本题可抽象为:
已知:∠DAB=60?,DE=0.5
m,AD=AB=3
m,△ACB
为直角三角形,求
CE
的长度.
0.5
m
3
m
A
B
C
D
E
60°
二、探究新知
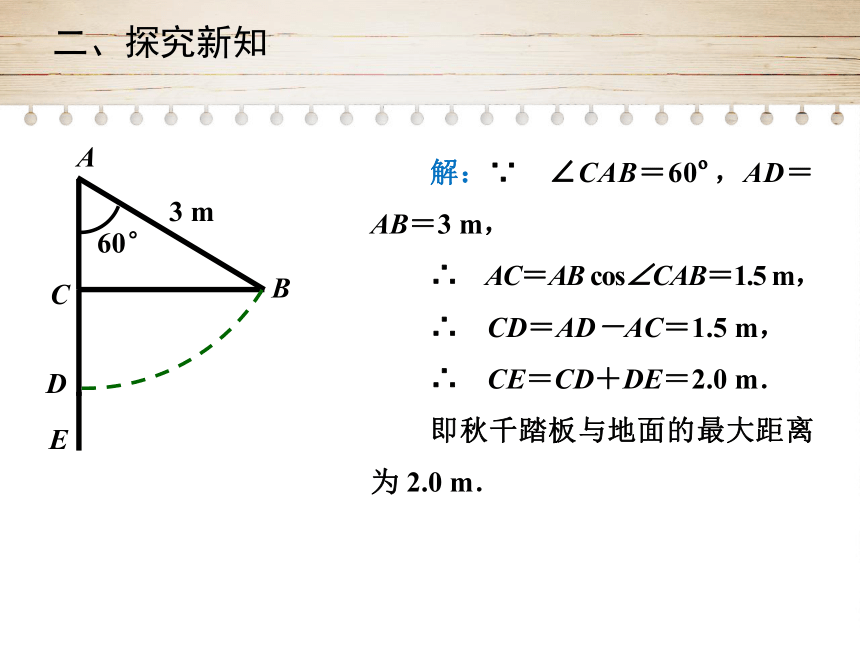
解:∵ ∠CAB=60?,AD=AB=3
m,
∴ AC=AB
cos∠CAB=1.5
m,
∴ CD=AD-AC=1.5
m,
∴ CE=CD+DE=2.0
m.
即秋千踏板与地面的最大距离为
2.0
m.
3
m
A
B
D
E
60°
C
二、探究新知
解决有关仰俯角的问题
在进行测量时,
从下向上看,视线与水平线上方的夹角叫做仰角;
从上往下看,视线与水平线下方的夹角叫做俯角.
二、探究新知
例
2 热气球的探测器显示,从热气球看一栋楼顶部的仰角为
30?,看这栋楼底部的俯角为
60?,热气球与楼的水平距离为
120
m,这栋楼有多高?(结果取整数)
A
B
C
D
α=30°
120
仰角
俯角
水平线
β=60°
二、探究新知
解:α=30?,β=60?,AD=120.
答:这栋楼高约为
277
m.
二、探究新知
练习
2 建筑物
BC
上有一旗杆
AB,由距
BC
40
m的
D处观察旗杆顶部
A
的仰角为
54?,观察底部
B
的仰角为
45?,求旗杆的高度(结果保留小数点后一位).
二、探究新知
解:由题知∠ACD=90?,∠BDC=45?
,
∴ BC=CD=40.
在
Rt△ACD
中,
=40·tan
54°≈1.38×40=55.2
(m).
∴ AB=AC-BC=55.2-40=15.2(m).
答:旗杆的高约为
15.2
m.
A
B
C
D
40
m
54°
45°
二、探究新知
梳理
利用解直角三角形解决实际问题的一般过程有哪些?
1.将实际问题抽象为数学问题;
画出平面图形,转化为解直角三角形的问题.
2.根据条件的特点,适当选用锐角三角函数等去解直角三角形;
3.得到数学问题的答案;
4.得到实际问题的答案.
三、课堂小结
解直角三角形的应用
解直角三角形实际应用的一般过程
运用解直角三角形解决仰角、俯角问题
仰角、俯角的概念
四、课堂训练
1.一次台风将一棵大树刮断,经测量,大树刮断一端的着地点
A
到树根部
C
的距离为
4
米,倒下部分
AB
与地平面
AC
的夹角为
45?,则这棵大树高是_________米.
四、课堂训练
2.为测量松树
AB
的高度,一个人站在距松树
15
米的E
处,测得仰角∠ACD=52?,已知人的高度是
1.72
米,则树高_________(精确到
0.1
米).
A
D
B
E
C
20.9
米
四、课堂训练
3.如图,沿
AC
方向开山修路.为了加快施工进度,要在小山的另一边同时施工,从
AC
上的一点
B
取∠ABD=
140?,
BD=520
m
,
∠D=50?,那么开挖点
E
离
D
多远正好能使
A
,
C
,
E
成一直线(精确到
0.1
m).
50°
140°
520m
A
B
C
E
D
四、课堂训练
解:要使
A,C,E
成一直线,则
∠ABD
是△BDE
的外角.
∴ ∠BED=∠ABD-∠D=90?.
cos∠BDE=
∴ DE=BD?cos∠BDE=520×cos
50?≈334.2(m).
答:开挖点
E
离点
D
334.2
m
正好能使
A,C,E
成一直线.
四、课堂训练
4.如图,直升飞机在高为
200
米的大楼
AB
上方
P
点处,
从大楼的顶部和底部测得飞机的仰角为
30?和
45?,则飞机的高度
PO=__________________.
45°
30°
O
B
A
P
四、课堂训练
5.如图,直升飞机在长
400
米的跨江大桥
AB
的上方
P点处,在大桥的两端测得飞机的仰角分别为
37?和
45?,求飞机的高度.(结果取整数.参考数据:sin
37?≈0.8,cos
37?≈0.6,tan
37?≈0.75)
A
B
37°
45°
400米
P
O
四、课堂训练
解:作
PO⊥AB
交
AB
延长线于
O.设
PO=x
米,
在
Rt△POB
中,∠PBO=45?,OB=PO=x
米.
在
Rt△POA
中,∠PAB=37?,
即
故飞机的高度为
1
200
米.
A
B
37°
45°
400米
P
O
四、课堂训练
梳理:仰角、俯角问题的常见基本模型:
模型二
A
B
C
D
α
β
模型三
A
B
C
D
α
β
A
B
C
D
模型四
α
β
模型一
A
D
B
E
C
α
五、作业
教科书习题
28.2
第
3,4,8
题.
第二十八章 锐角三角函数
28.2 解直角三角形及其应用
28.2.2 应用举例
第一课时
一、情景导入
高跟鞋深受很多女性的喜爱,但有时候,如果鞋跟太高,不仅腿脚容易疲劳,还有可能会“闹笑话”.
专家认为当人的脚掌长为
15
cm,鞋跟约在
3
cm
左右高度感觉最舒适,由此你能算出高跟鞋的鞋底与地面的夹角吗?生活中解直角三角形的应用非常广泛.
二、探究新知
例
1 2012
年
6
月
18
日,
“神州”九号载人航天飞船与“天宫”一号目标飞行器成功实现交会对接.“神州”九号与“天宫”一号的组合体在离地球表面
343
km
的圆形轨道上运行.如图,当组合体运行到离地球表面
P
点的正上方时,从中能直接看到的地球表面最远的点在什么位置?最远点与
P
点的距离是多少(地球半径约为
6400
km,
π
取
3.142
,
结果取整数)?
二、探究新知
FQ是☉O的切线,∠FQO为直角.
最远点
·
P
Q
O
α
F
求
的长,要先求∠POQ的度数
二、探究新知
解:连接
OQ,设∠POQ=α,
∵ FQ
是
☉O
的切线,
∴ △FOQ
是直角三角形.
∴
的长为
·
P
Q
O
二、探究新知
当飞船在
P
点正上方时,从飞船观测地球时的最远点距离
P
点约
2
051
km.
二、探究新知
练习
1 如图,秋千链子的长度为
3
m,静止时的秋千踏板(大小忽略不计)距地面
0.5
m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为
60?,则秋千踏板与地面的最大距离为多少?
0.5
m
3
m
60°
?
?
二、探究新知
分析:根据题意,可知秋千踏板与地面的最大距离为CE的长度.因此,本题可抽象为:
已知:∠DAB=60?,DE=0.5
m,AD=AB=3
m,△ACB
为直角三角形,求
CE
的长度.
0.5
m
3
m
A
B
C
D
E
60°
二、探究新知
解:∵ ∠CAB=60?,AD=AB=3
m,
∴ AC=AB
cos∠CAB=1.5
m,
∴ CD=AD-AC=1.5
m,
∴ CE=CD+DE=2.0
m.
即秋千踏板与地面的最大距离为
2.0
m.
3
m
A
B
D
E
60°
C
二、探究新知
解决有关仰俯角的问题
在进行测量时,
从下向上看,视线与水平线上方的夹角叫做仰角;
从上往下看,视线与水平线下方的夹角叫做俯角.
二、探究新知
例
2 热气球的探测器显示,从热气球看一栋楼顶部的仰角为
30?,看这栋楼底部的俯角为
60?,热气球与楼的水平距离为
120
m,这栋楼有多高?(结果取整数)
A
B
C
D
α=30°
120
仰角
俯角
水平线
β=60°
二、探究新知
解:α=30?,β=60?,AD=120.
答:这栋楼高约为
277
m.
二、探究新知
练习
2 建筑物
BC
上有一旗杆
AB,由距
BC
40
m的
D处观察旗杆顶部
A
的仰角为
54?,观察底部
B
的仰角为
45?,求旗杆的高度(结果保留小数点后一位).
二、探究新知
解:由题知∠ACD=90?,∠BDC=45?
,
∴ BC=CD=40.
在
Rt△ACD
中,
=40·tan
54°≈1.38×40=55.2
(m).
∴ AB=AC-BC=55.2-40=15.2(m).
答:旗杆的高约为
15.2
m.
A
B
C
D
40
m
54°
45°
二、探究新知
梳理
利用解直角三角形解决实际问题的一般过程有哪些?
1.将实际问题抽象为数学问题;
画出平面图形,转化为解直角三角形的问题.
2.根据条件的特点,适当选用锐角三角函数等去解直角三角形;
3.得到数学问题的答案;
4.得到实际问题的答案.
三、课堂小结
解直角三角形的应用
解直角三角形实际应用的一般过程
运用解直角三角形解决仰角、俯角问题
仰角、俯角的概念
四、课堂训练
1.一次台风将一棵大树刮断,经测量,大树刮断一端的着地点
A
到树根部
C
的距离为
4
米,倒下部分
AB
与地平面
AC
的夹角为
45?,则这棵大树高是_________米.
四、课堂训练
2.为测量松树
AB
的高度,一个人站在距松树
15
米的E
处,测得仰角∠ACD=52?,已知人的高度是
1.72
米,则树高_________(精确到
0.1
米).
A
D
B
E
C
20.9
米
四、课堂训练
3.如图,沿
AC
方向开山修路.为了加快施工进度,要在小山的另一边同时施工,从
AC
上的一点
B
取∠ABD=
140?,
BD=520
m
,
∠D=50?,那么开挖点
E
离
D
多远正好能使
A
,
C
,
E
成一直线(精确到
0.1
m).
50°
140°
520m
A
B
C
E
D
四、课堂训练
解:要使
A,C,E
成一直线,则
∠ABD
是△BDE
的外角.
∴ ∠BED=∠ABD-∠D=90?.
cos∠BDE=
∴ DE=BD?cos∠BDE=520×cos
50?≈334.2(m).
答:开挖点
E
离点
D
334.2
m
正好能使
A,C,E
成一直线.
四、课堂训练
4.如图,直升飞机在高为
200
米的大楼
AB
上方
P
点处,
从大楼的顶部和底部测得飞机的仰角为
30?和
45?,则飞机的高度
PO=__________________.
45°
30°
O
B
A
P
四、课堂训练
5.如图,直升飞机在长
400
米的跨江大桥
AB
的上方
P点处,在大桥的两端测得飞机的仰角分别为
37?和
45?,求飞机的高度.(结果取整数.参考数据:sin
37?≈0.8,cos
37?≈0.6,tan
37?≈0.75)
A
B
37°
45°
400米
P
O
四、课堂训练
解:作
PO⊥AB
交
AB
延长线于
O.设
PO=x
米,
在
Rt△POB
中,∠PBO=45?,OB=PO=x
米.
在
Rt△POA
中,∠PAB=37?,
即
故飞机的高度为
1
200
米.
A
B
37°
45°
400米
P
O
四、课堂训练
梳理:仰角、俯角问题的常见基本模型:
模型二
A
B
C
D
α
β
模型三
A
B
C
D
α
β
A
B
C
D
模型四
α
β
模型一
A
D
B
E
C
α
五、作业
教科书习题
28.2
第
3,4,8
题.
