人教版九年级下册28.2.2解直角三角形应用举例(第2课时)课件(14张PPT)
文档属性
| 名称 | 人教版九年级下册28.2.2解直角三角形应用举例(第2课时)课件(14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 07:04:57 | ||
图片预览


文档简介
(共17张PPT)
第二十八章
锐角三角函数
28.2
解直角三角形及其应用
28.2.2
应用举例
第二课时
一、情景导入
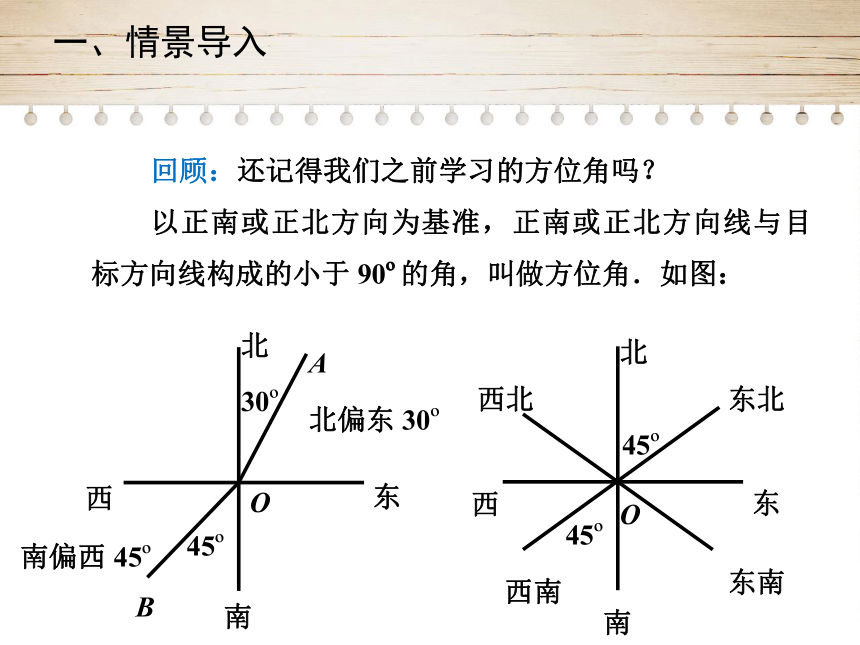
回顾:还记得我们之前学习的方位角吗?
以正南或正北方向为基准,正南或正北方向线与目标方向线构成的小于
90?的角,叫做方位角.如图:
30?
45?
B
O
A
东
西
北
南
北偏东
30?
南偏西
45?
45?
45?
西南
O
东北
东
西
北
南
西北
东南
一、情景导入
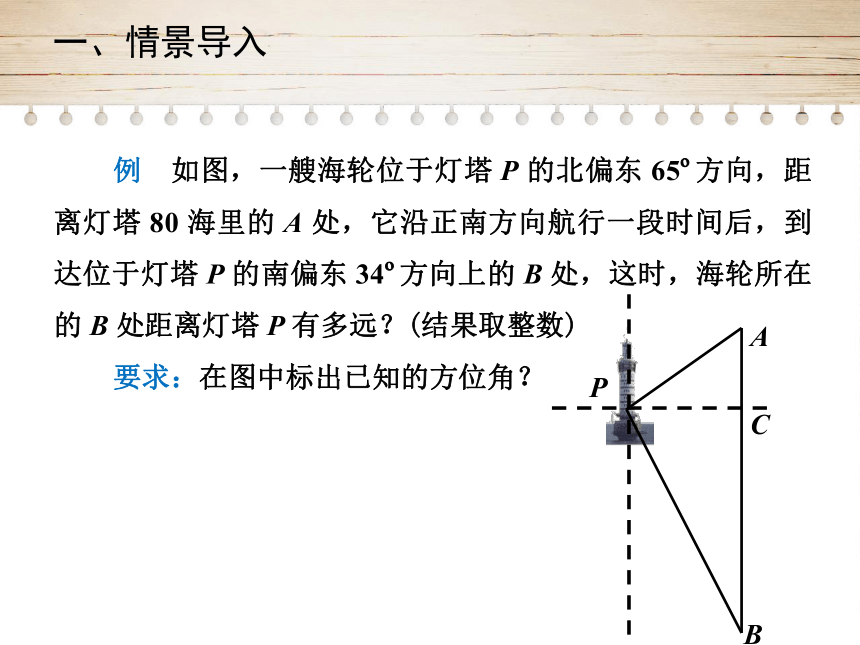
例 如图,一艘海轮位于灯塔
P
的北偏东
65?方向,距离灯塔
80
海里的
A
处,它沿正南方向航行一段时间后,到达位于灯塔
P
的南偏东
34?方向上的
B
处,这时,海轮所在的
B
处距离灯塔
P
有多远?(结果取整数)
要求:在图中标出已知的方位角?
P
B
C
A
二、探究新知
解:在
Rt△APC
中,
PC=PA·cos(90?-65?)
=80×cos
25?≈72.505.
在
Rt△BPC
中,∠B=34?,
答:当海轮到达位于灯塔
P
的南偏东
34?方向时,它距离灯塔
P
大约
130
n
mile
.
二、探究新知
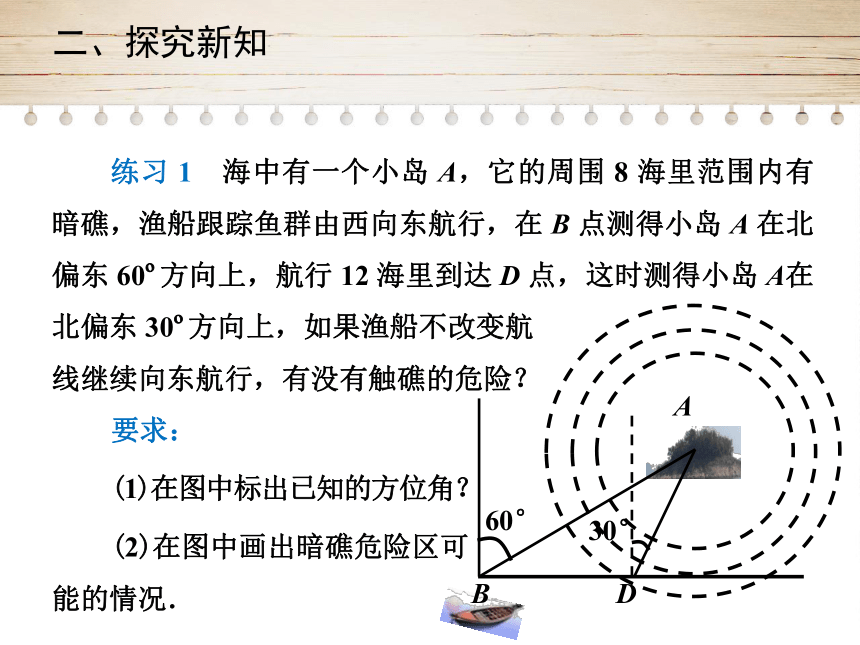
练习
1 海中有一个小岛
A,它的周围
8
海里范围内有暗礁,渔船跟踪鱼群由西向东航行,在
B
点测得小岛
A
在北偏东
60?方向上,航行
12
海里到达
D
点,这时测得小岛
A在北偏东
30?方向上,如果渔船不改变航
线继续向东航行,有没有触礁的危险?
要求:
(1)在图中标出已知的方位角?
(2)在图中画出暗礁危险区可
能的情况.
B
A
D
60°
30°
二、探究新知
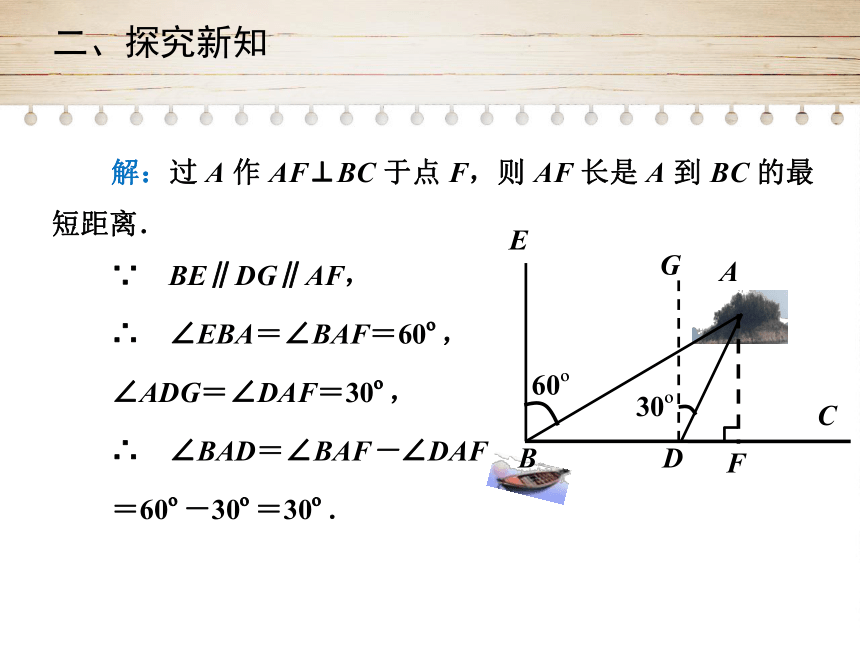
解:过
A
作
AF⊥BC
于点
F,则
AF
长是
A
到
BC
的最短距离.
∵ BE∥DG∥AF,
∴ ∠EBA=∠BAF=60?,
∠ADG=∠DAF=30?,
∴ ∠BAD=∠BAF-∠DAF
=60?-30?=30?.
F
C
B
A
D
60?
30?
E
G
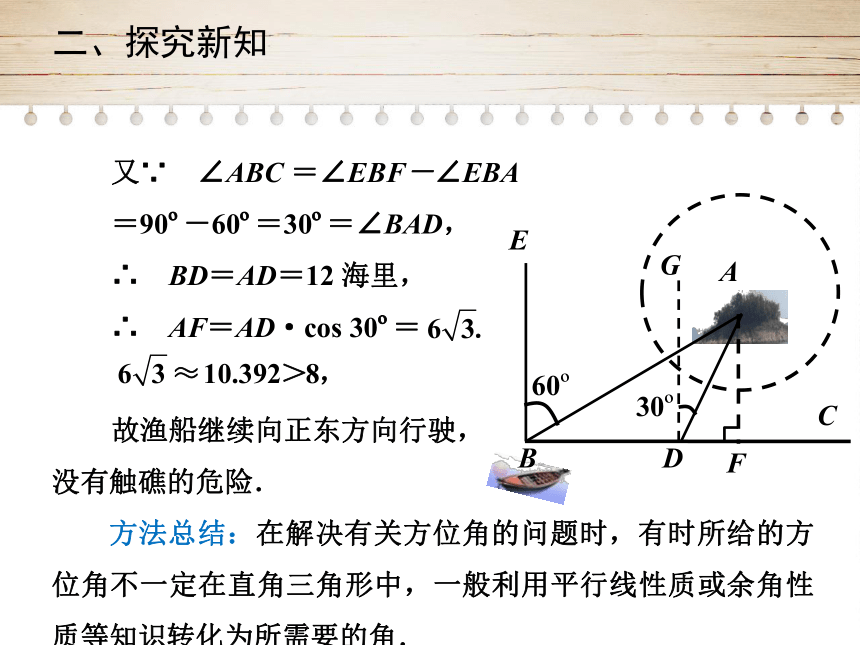
二、探究新知
又∵ ∠ABC
=∠EBF-∠EBA
=90?-60?=30?=∠BAD,
∴ BD=AD=12
海里,
∴ AF=AD·cos
30?=
故渔船继续向正东方向行驶,
没有触礁的危险.
方法总结:在解决有关方位角的问题时,有时所给的方位角不一定在直角三角形中,一般利用平行线性质或余角性质等知识转化为所需要的角.
F
C
B
A
D
60?
30?
E
G
二、探究新知
练习
2 如图,某渔船如图所示,某渔船在海面上朝正东方向匀速航行,在
A
处观测到灯塔
M
在北偏东
60?方向上,航行半小时后到达
B
处,此时观测到灯塔
M
在北偏东
30?方向上,那么该船继续航行到达离灯塔距离最近的位置所需的时间是_________.
15
分钟
北
北
东
60?
30?
M
B
A
三、课堂小结
利用方位角解直角三角形
方位角的概念
运用解直角三角形解决方位角问题
四、课堂训练
1.如图,C
岛在
A
岛的北偏东
50?方向,C
岛在
B
岛的北偏西
40?方向,则从
C
岛看
A,B
两岛的视角∠ACB
等于_______.
90?
四、课堂训练
2.如图,在某监测点
B
处望见一艘正在作业的渔船在南偏西
15?方向的
A
处,若渔船沿北偏西
75?方向以
40
海里/时的速度航行,航行半小时后到达
C
处,在
C
处观测到监测点
B
在
C
的北偏东
60?方向上,则
B,C
之间的距离为__________.
(参考数据:
≈1.732,
≈1.414)
28.28
海里
60°
75°
15°
A
B
C
200
km
四、课堂训练
3.如图,A、B
两城市相距
200
km.现计划在这两座城市间修筑一条高速公路(即线段
AB),经测量,森林保护中心
P
在
A
城市的北偏东
30?和
B
城市的北偏西
45?的方向上.已知森林保护区的范围在以
P
点为圆心,100
km
为半径的圆形区域内,请问:计划修筑的这条高速公路会不会穿越保护区(参考数据:
≈1.732,
≈1.414).
四、课堂训练
解:过点
P
作
PC⊥AB,C
是垂足.
则∠APC=30?,∠BPC=45?,
AC=PC·tan
30?,
BC=PC·tan
45?.
∵ AC+BC=AB,
∴ PC·tan
30?+PC·tan
45?=200,
即
PC+PC=200,
解得
PC
≈
126.8
km>100
km.
方法总结:直角三角形中没有确定的边长时,经常通过设未知数找相等关系建立方程来求解.
200
km
C
四、课堂训练
4.如图,我国两艘海监船
A,B
在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船
C,此时,B
船在
A
船的正南方向
5
海里处,A
船测得渔船
C
在其南偏东
45?方向,B
船测得渔船
C
在
其南偏东
53?方向,已知
A
船的航速为
30
海里/时,B
船的航速为
25
海里/时,
问
C
船至少要等待多长时间才能得到救
援?
(参考数据:sin
53?
≈
cos
53?
≈
tan
53?
≈
≈1.41.)
A
B
53?
45?
C
四、课堂训练
解:过点
C
作
CD⊥AB
于
D,设
AD=x
米.
则
BD=(x-5)米.
∵ 在
Rt△ACD
中,
∠DAC=45?,
∴ CD=AD=x
米.
∵ 在
Rt△BCD
中,
∠CBD=53?,
∴ tan
53?=
即
解得
x=20.
D
A
B
53?
45?
C
四、课堂训练
∴ CD=AD=20
米.
∴ CA=
≈28.2
,BC=
≈
25.
∴ A
船到
C
的时间:
B
船到
C
的时间:
∴ C
船至少要等待
0.94
小时才能得到救援.
五、作业
教科书习题
28.2
第
10,11
题.
第二十八章
锐角三角函数
28.2
解直角三角形及其应用
28.2.2
应用举例
第二课时
一、情景导入
回顾:还记得我们之前学习的方位角吗?
以正南或正北方向为基准,正南或正北方向线与目标方向线构成的小于
90?的角,叫做方位角.如图:
30?
45?
B
O
A
东
西
北
南
北偏东
30?
南偏西
45?
45?
45?
西南
O
东北
东
西
北
南
西北
东南
一、情景导入
例 如图,一艘海轮位于灯塔
P
的北偏东
65?方向,距离灯塔
80
海里的
A
处,它沿正南方向航行一段时间后,到达位于灯塔
P
的南偏东
34?方向上的
B
处,这时,海轮所在的
B
处距离灯塔
P
有多远?(结果取整数)
要求:在图中标出已知的方位角?
P
B
C
A
二、探究新知
解:在
Rt△APC
中,
PC=PA·cos(90?-65?)
=80×cos
25?≈72.505.
在
Rt△BPC
中,∠B=34?,
答:当海轮到达位于灯塔
P
的南偏东
34?方向时,它距离灯塔
P
大约
130
n
mile
.
二、探究新知
练习
1 海中有一个小岛
A,它的周围
8
海里范围内有暗礁,渔船跟踪鱼群由西向东航行,在
B
点测得小岛
A
在北偏东
60?方向上,航行
12
海里到达
D
点,这时测得小岛
A在北偏东
30?方向上,如果渔船不改变航
线继续向东航行,有没有触礁的危险?
要求:
(1)在图中标出已知的方位角?
(2)在图中画出暗礁危险区可
能的情况.
B
A
D
60°
30°
二、探究新知
解:过
A
作
AF⊥BC
于点
F,则
AF
长是
A
到
BC
的最短距离.
∵ BE∥DG∥AF,
∴ ∠EBA=∠BAF=60?,
∠ADG=∠DAF=30?,
∴ ∠BAD=∠BAF-∠DAF
=60?-30?=30?.
F
C
B
A
D
60?
30?
E
G
二、探究新知
又∵ ∠ABC
=∠EBF-∠EBA
=90?-60?=30?=∠BAD,
∴ BD=AD=12
海里,
∴ AF=AD·cos
30?=
故渔船继续向正东方向行驶,
没有触礁的危险.
方法总结:在解决有关方位角的问题时,有时所给的方位角不一定在直角三角形中,一般利用平行线性质或余角性质等知识转化为所需要的角.
F
C
B
A
D
60?
30?
E
G
二、探究新知
练习
2 如图,某渔船如图所示,某渔船在海面上朝正东方向匀速航行,在
A
处观测到灯塔
M
在北偏东
60?方向上,航行半小时后到达
B
处,此时观测到灯塔
M
在北偏东
30?方向上,那么该船继续航行到达离灯塔距离最近的位置所需的时间是_________.
15
分钟
北
北
东
60?
30?
M
B
A
三、课堂小结
利用方位角解直角三角形
方位角的概念
运用解直角三角形解决方位角问题
四、课堂训练
1.如图,C
岛在
A
岛的北偏东
50?方向,C
岛在
B
岛的北偏西
40?方向,则从
C
岛看
A,B
两岛的视角∠ACB
等于_______.
90?
四、课堂训练
2.如图,在某监测点
B
处望见一艘正在作业的渔船在南偏西
15?方向的
A
处,若渔船沿北偏西
75?方向以
40
海里/时的速度航行,航行半小时后到达
C
处,在
C
处观测到监测点
B
在
C
的北偏东
60?方向上,则
B,C
之间的距离为__________.
(参考数据:
≈1.732,
≈1.414)
28.28
海里
60°
75°
15°
A
B
C
200
km
四、课堂训练
3.如图,A、B
两城市相距
200
km.现计划在这两座城市间修筑一条高速公路(即线段
AB),经测量,森林保护中心
P
在
A
城市的北偏东
30?和
B
城市的北偏西
45?的方向上.已知森林保护区的范围在以
P
点为圆心,100
km
为半径的圆形区域内,请问:计划修筑的这条高速公路会不会穿越保护区(参考数据:
≈1.732,
≈1.414).
四、课堂训练
解:过点
P
作
PC⊥AB,C
是垂足.
则∠APC=30?,∠BPC=45?,
AC=PC·tan
30?,
BC=PC·tan
45?.
∵ AC+BC=AB,
∴ PC·tan
30?+PC·tan
45?=200,
即
PC+PC=200,
解得
PC
≈
126.8
km>100
km.
方法总结:直角三角形中没有确定的边长时,经常通过设未知数找相等关系建立方程来求解.
200
km
C
四、课堂训练
4.如图,我国两艘海监船
A,B
在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船
C,此时,B
船在
A
船的正南方向
5
海里处,A
船测得渔船
C
在其南偏东
45?方向,B
船测得渔船
C
在
其南偏东
53?方向,已知
A
船的航速为
30
海里/时,B
船的航速为
25
海里/时,
问
C
船至少要等待多长时间才能得到救
援?
(参考数据:sin
53?
≈
cos
53?
≈
tan
53?
≈
≈1.41.)
A
B
53?
45?
C
四、课堂训练
解:过点
C
作
CD⊥AB
于
D,设
AD=x
米.
则
BD=(x-5)米.
∵ 在
Rt△ACD
中,
∠DAC=45?,
∴ CD=AD=x
米.
∵ 在
Rt△BCD
中,
∠CBD=53?,
∴ tan
53?=
即
解得
x=20.
D
A
B
53?
45?
C
四、课堂训练
∴ CD=AD=20
米.
∴ CA=
≈28.2
,BC=
≈
25.
∴ A
船到
C
的时间:
B
船到
C
的时间:
∴ C
船至少要等待
0.94
小时才能得到救援.
五、作业
教科书习题
28.2
第
10,11
题.
