人教版九年级下册28.2.2解直角三角形应用举例(第3课时)课件(19张PPT)
文档属性
| 名称 | 人教版九年级下册28.2.2解直角三角形应用举例(第3课时)课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
第二十八章 锐角三角函数
28.2 解直角三角形及其应用
28.2.2 应用举例
第三课时
一、情景导入
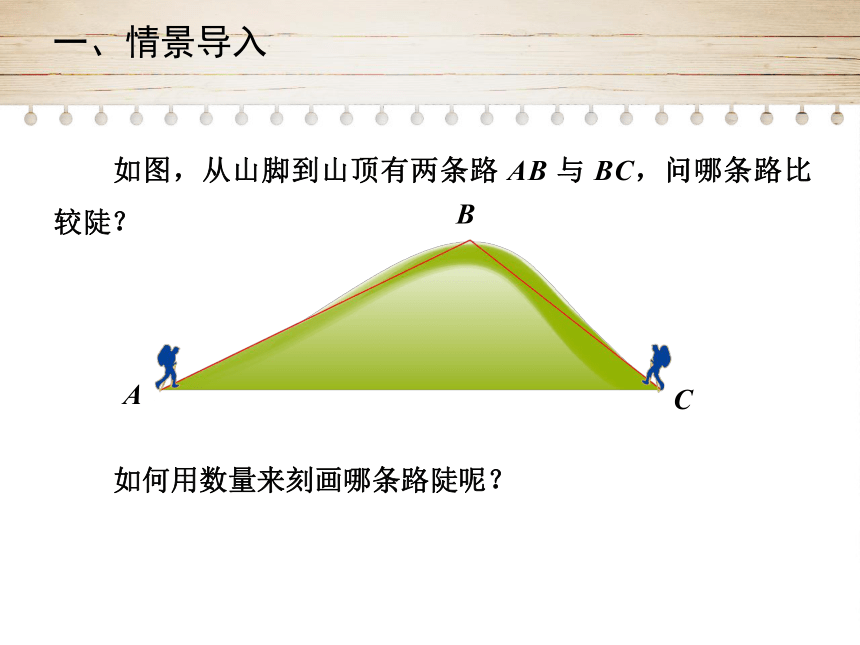
如图,从山脚到山顶有两条路
AB
与
BC,问哪条路比较陡?
如何用数量来刻画哪条路陡呢?
A
B
C
二、探究新知
知识链接
1.坡面与水平面的夹角叫做坡角,记作α
,如上图.
2.坡面的铅垂高度(h)和水平长度(l)的比叫做坡面的坡度(或坡比)
,记作
i,即
i=h∶l
,如上图.
坡度通常写成
1∶m
的形式,如
i=1∶6.
α
i=h
:
l
l
h
坡面
二、探究新知
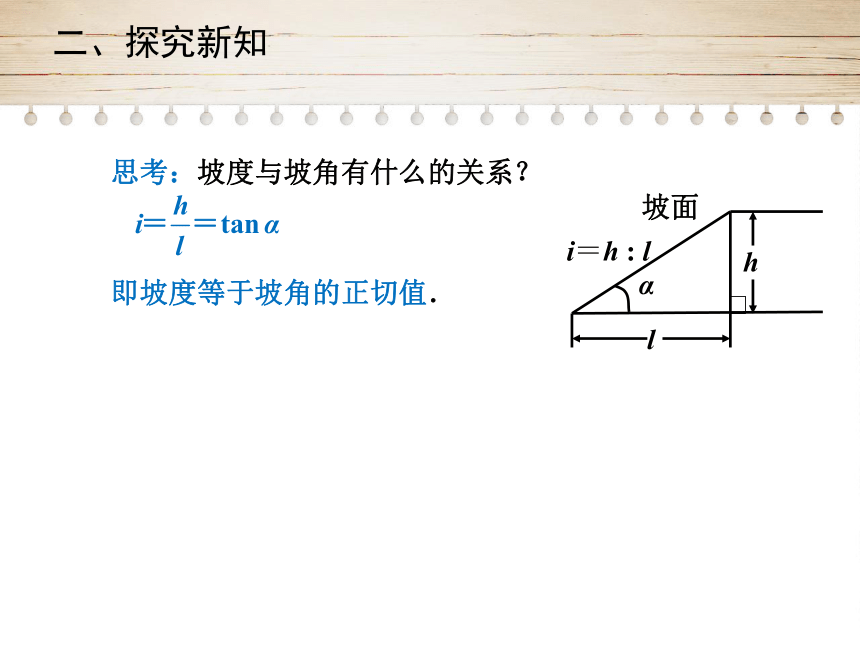
思考:坡度与坡角有什么的关系?
即坡度等于坡角的正切值.
α
i=h
:
l
l
h
坡面
二、探究新知
1.斜坡的坡度是
,则坡角
α
=_______
度.
2.斜坡的坡角是
45?,则坡比是
_______.
3.
斜坡长是
12
米,坡高
6
米,则坡比是______.
30
1∶1
二、探究新知
4.如图,一山坡的坡度为
i=1∶2.小刚从山脚
A
出发,
沿山坡向上走了
240
m
到达点
C.小刚上升了大约______米(精确到
0.1
m).
107.3
二、探究新知
例
水库大坝的横断面是梯形,坝顶宽
6
m,坝高
5
m,斜坡
AB
的坡度
i=1∶3,斜坡
CD
的坡度
i=1∶2.5,求:
(1)斜坡
CD
的坡角
α
(精确到
1?)
;
(2)坝底
AD
与斜坡
AB
的长度(精确到
0.1
m).
A
D
B
C
i=1:2.5
5
6
α
i=1:3
二、探究新知
解:
(1)
斜坡
CD
的坡度
i=tanα=1∶2.5=0.4,
由计算器可算得
α≈22?.
故斜坡
CD
的坡角
α
为
22?.
二、探究新知
(2)过点
B
作
BE⊥AD
于点
E,
过点
C
作
CF⊥AD
于点
F,
由题知
BE=CF=5
m,
EF=BC=6
m.
在
Rt△ABE
中,
∴ AE=3BE=3×5=15(m).
在
Rt△DCF
中,同理可得
∴ FD=2.5CF=2.5×5=12.5(m).
A
D
B
C
i=1∶2.5
5
6
α
i=1∶3
E
F
二、探究新知
则
AD=AE+EF+FD
=15+6+12.5=33.5(m).
在
Rt△ABE
中,由勾股定理可得
故坝底
AD
的长度为
33.5
m,斜坡
AB
的长度为
15.8
m.
二、探究新知
5.如图,拦水坝的横断面为梯形
ABCD(图中
i
是指坡面的铅直高度与水平宽度的比),由图中数据可得∠C≈_______,斜坡
AB_______
m(精确到
0.1).
B
A
D
F
E
C
6
m
i=1:3
i=1:1.5
18.3?
10.8
三、课堂小结
利用坡角解直角三角形
坡度坡角的概念
运用解直角三角形解决坡度坡角问题
四、课堂训练
1.如图,小明周末上山踏青,他从山脚处的
B
点出发时,测得坡面
AB
的坡度为
1∶2,走
米到达山顶
A
处.这时,他发现山的另一坡面
AC
的最低点
C
的俯角是
30?,则
BC=______________
米.
A
C
B
D
四、课堂训练
2.如图,小王在长江边某瞭望台
D
处,测得江面上的渔船
A
的俯角为
40?,若
DE=3
米,CE=2
米,CE
平行于江面
AB,迎水坡
BC
的坡度
i=1∶0.75,坡长
BC=10
米,则此时
AB
的长约为( ).(参考数据:sin
40?≈0.64,
cos
40?≈0.77,tan
40?≈0.84)
A.5.1
米
B.6.3
米
C.7.1
米
D.9.2
米
A
D
C
E
A
B
40?
i=1∶0.75
四、课堂训练
3.如图,某工程队准备在山坡(山坡视为直线)上修一条路,需测量山坡的坡度,即
tanα
值.现在山坡
P
处
(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖
C
的仰角为
37?,塔底
B
的仰角为
26.6?.已知塔高
BC=80
米,塔所在的山高
OB=220
米,
OA=200
米,
O,B,C,A,P
在同一平面,求山坡坡度.(参考数据
sin
26.6?≈0.45,tan
26.6?≈0.50;sin
37?≈0.60,tan
37?≈0.75)
四、课堂训练
解:过点
P
作
PD⊥OC
于
D
,
PE⊥OA
于
E
,
则四边形
ODPE
为矩形.
在
Rt△PBD
中,
∵ ∠BDP=90?,∠BPD=26.6?,
∴ BD=PD·tan∠BPD
=PD·tan
26.6?.
在
Rt△CPD
中,
∵ ∠CDP=90?,∠CPD=37?,
∴ CD=PD·tan∠CPD=PD·tan
37?.
D
E
四、课堂训练
∵ CD-BD=BC,
∴ PD·tan
37?-PD·tan
26.6?=80.
∴ 0.75PD-0.50PD=80.
解得 PD=320.
∴ BD=PD·tan
26.6?≈320×0.50=160.
∴ PE=OD=OB-BD=60.
四、课堂训练
∵ OE=PD=320,
∴ AE=OE-OA=320-200=120.
∴ tan
α=
=0.5.
∴ 山坡的坡度为
1∶2.
五、作业
教科书习题
28.2
第
5,9
题.
第二十八章 锐角三角函数
28.2 解直角三角形及其应用
28.2.2 应用举例
第三课时
一、情景导入
如图,从山脚到山顶有两条路
AB
与
BC,问哪条路比较陡?
如何用数量来刻画哪条路陡呢?
A
B
C
二、探究新知
知识链接
1.坡面与水平面的夹角叫做坡角,记作α
,如上图.
2.坡面的铅垂高度(h)和水平长度(l)的比叫做坡面的坡度(或坡比)
,记作
i,即
i=h∶l
,如上图.
坡度通常写成
1∶m
的形式,如
i=1∶6.
α
i=h
:
l
l
h
坡面
二、探究新知
思考:坡度与坡角有什么的关系?
即坡度等于坡角的正切值.
α
i=h
:
l
l
h
坡面
二、探究新知
1.斜坡的坡度是
,则坡角
α
=_______
度.
2.斜坡的坡角是
45?,则坡比是
_______.
3.
斜坡长是
12
米,坡高
6
米,则坡比是______.
30
1∶1
二、探究新知
4.如图,一山坡的坡度为
i=1∶2.小刚从山脚
A
出发,
沿山坡向上走了
240
m
到达点
C.小刚上升了大约______米(精确到
0.1
m).
107.3
二、探究新知
例
水库大坝的横断面是梯形,坝顶宽
6
m,坝高
5
m,斜坡
AB
的坡度
i=1∶3,斜坡
CD
的坡度
i=1∶2.5,求:
(1)斜坡
CD
的坡角
α
(精确到
1?)
;
(2)坝底
AD
与斜坡
AB
的长度(精确到
0.1
m).
A
D
B
C
i=1:2.5
5
6
α
i=1:3
二、探究新知
解:
(1)
斜坡
CD
的坡度
i=tanα=1∶2.5=0.4,
由计算器可算得
α≈22?.
故斜坡
CD
的坡角
α
为
22?.
二、探究新知
(2)过点
B
作
BE⊥AD
于点
E,
过点
C
作
CF⊥AD
于点
F,
由题知
BE=CF=5
m,
EF=BC=6
m.
在
Rt△ABE
中,
∴ AE=3BE=3×5=15(m).
在
Rt△DCF
中,同理可得
∴ FD=2.5CF=2.5×5=12.5(m).
A
D
B
C
i=1∶2.5
5
6
α
i=1∶3
E
F
二、探究新知
则
AD=AE+EF+FD
=15+6+12.5=33.5(m).
在
Rt△ABE
中,由勾股定理可得
故坝底
AD
的长度为
33.5
m,斜坡
AB
的长度为
15.8
m.
二、探究新知
5.如图,拦水坝的横断面为梯形
ABCD(图中
i
是指坡面的铅直高度与水平宽度的比),由图中数据可得∠C≈_______,斜坡
AB_______
m(精确到
0.1).
B
A
D
F
E
C
6
m
i=1:3
i=1:1.5
18.3?
10.8
三、课堂小结
利用坡角解直角三角形
坡度坡角的概念
运用解直角三角形解决坡度坡角问题
四、课堂训练
1.如图,小明周末上山踏青,他从山脚处的
B
点出发时,测得坡面
AB
的坡度为
1∶2,走
米到达山顶
A
处.这时,他发现山的另一坡面
AC
的最低点
C
的俯角是
30?,则
BC=______________
米.
A
C
B
D
四、课堂训练
2.如图,小王在长江边某瞭望台
D
处,测得江面上的渔船
A
的俯角为
40?,若
DE=3
米,CE=2
米,CE
平行于江面
AB,迎水坡
BC
的坡度
i=1∶0.75,坡长
BC=10
米,则此时
AB
的长约为( ).(参考数据:sin
40?≈0.64,
cos
40?≈0.77,tan
40?≈0.84)
A.5.1
米
B.6.3
米
C.7.1
米
D.9.2
米
A
D
C
E
A
B
40?
i=1∶0.75
四、课堂训练
3.如图,某工程队准备在山坡(山坡视为直线)上修一条路,需测量山坡的坡度,即
tanα
值.现在山坡
P
处
(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖
C
的仰角为
37?,塔底
B
的仰角为
26.6?.已知塔高
BC=80
米,塔所在的山高
OB=220
米,
OA=200
米,
O,B,C,A,P
在同一平面,求山坡坡度.(参考数据
sin
26.6?≈0.45,tan
26.6?≈0.50;sin
37?≈0.60,tan
37?≈0.75)
四、课堂训练
解:过点
P
作
PD⊥OC
于
D
,
PE⊥OA
于
E
,
则四边形
ODPE
为矩形.
在
Rt△PBD
中,
∵ ∠BDP=90?,∠BPD=26.6?,
∴ BD=PD·tan∠BPD
=PD·tan
26.6?.
在
Rt△CPD
中,
∵ ∠CDP=90?,∠CPD=37?,
∴ CD=PD·tan∠CPD=PD·tan
37?.
D
E
四、课堂训练
∵ CD-BD=BC,
∴ PD·tan
37?-PD·tan
26.6?=80.
∴ 0.75PD-0.50PD=80.
解得 PD=320.
∴ BD=PD·tan
26.6?≈320×0.50=160.
∴ PE=OD=OB-BD=60.
四、课堂训练
∵ OE=PD=320,
∴ AE=OE-OA=320-200=120.
∴ tan
α=
=0.5.
∴ 山坡的坡度为
1∶2.
五、作业
教科书习题
28.2
第
5,9
题.
