2.5 矩形 习题课件（共11张PPT）

(共11张PPT)
湘教版·八年级下册
上课课件
第2章
四边形
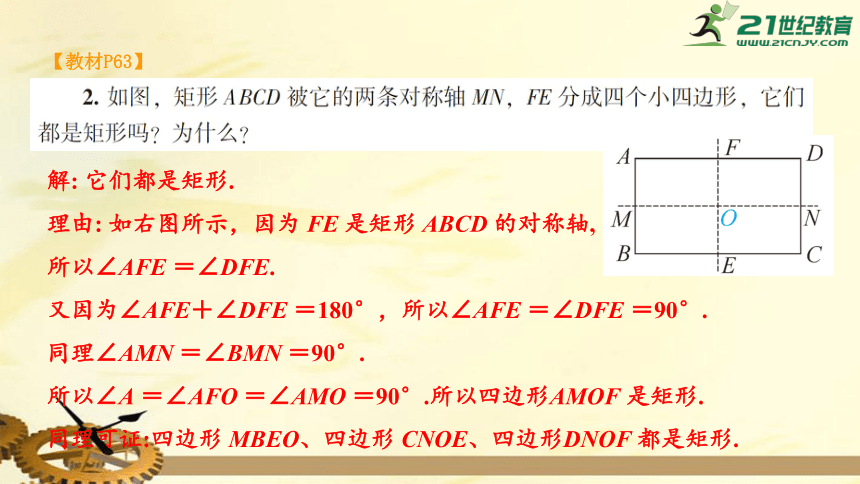
【教材P63】
解：∵
EF⊥FC，
∴∠AFE+∠DFC
=
90°.
又∠DCF
+∠DFC
=
90°
∴∠DCF
=∠AFE.
又∠A=∠D
=
90°，EF
=
FC,
∴Rt△FAE≌
Rt△CDF.
∴AE
=
DF
=
4
cm.
【教材P63】
解:
它们都是矩形.
理由:
如右图所示，因为
FE
是矩形
ABCD
的对称轴,
所以∠AFE
＝∠DFE.
又因为∠AFE＋∠DFE
＝180°，所以∠AFE
＝∠DFE
＝90°.
同理∠AMN
＝∠BMN
＝90°.
所以∠A
＝∠AFO
＝∠AMO
＝90°.所以四边形AMOF
是矩形.
同理可证:四边形
MBEO、四边形
CNOE、四边形DNOF
都是矩形.
【教材P63】
证明：因为四边形ABCD
为平行四边形,所以AB
＝DC.
又因为M
是AD
的中点,所以AM
＝DM.
在△ABM
和△DCM
中,
AB
＝DC,
AM
＝DM,BM
＝CM,
所以△ABM≌△DCM(SSS).所以∠A
＝∠D.
因为AB∥DC,所以∠A＋∠D
＝180°.
所以∠A
＝∠D
＝90°.
所以□
ABCD
是矩形(有一个角是直角的平行四边形是矩形).
【教材P64】
证明:
因为△ABC
是直角三角形,
BO
是斜边AC
上的中线,
所以BO
＝AO
＝CO
＝
AC,
所以AC
＝2BO.
又因为OD
＝OB,
所以四边形
ABCD
是平行四边形.
因为BD
＝2BO,所以BD
＝AC.
所以
□
ABCD
是矩形(对角线相等的平行四边形是矩形).
【教材P64】
解:如右图所示，连接
BE.
因为AD
＝4
cm,
设AE
＝x
cm,则DE
＝(4－x)cm.
又因为
EF
是
BD
的垂直平分线,
所以BE
＝DE
＝(4－x)cm.
在矩形ABCD中,∠A＝90°,
在Rt△ABE
中,由勾股定理,
得AE2
＋AB2
＝BE2
，
【教材P64】
证明:在
□
ABCD
中,因为
AB∥CD,
所以∠ABC＋∠BCD
＝180°.
又因为
BH
平分∠ABC,CH
平分∠BCD,
所以∠HBC
＝
∠ABC,
∠HCB
＝
∠BCD,
所以∠HBC＋∠HCB
＝
∠ABC＋
∠BCD
＝
×180°
＝
90°.
所以∠BHC
＝90°.同理可证:∠HEF
＝∠EFG
＝
90°.
所以四边形
EFGH
是矩形.
【教材P64】
证明:
因为四边形
ABCD
是矩形,
所以OA
＝OB
＝OC
＝OD
＝
AC
＝
BD.
又因为E,F,G,H
分别是OA,OB,OC,OD
的中点,
所以
OE
＝
OA,
OF
＝
OB,
OG
＝
OC,
OH
＝
OD.
所以
OE
＝OF
＝OG
＝OH
＝
EG
＝
FH.
由
OE
＝OG,
OF
＝
OH
得四边形
EFGH
是平行四边形.
由EG
＝FH
得
□
EFGH
是矩形(对角线相等的平行四边形是矩形).
课后作业
1.从课后习题中选取；
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网（www.21cnjy.com)
中小学教育资源网站
有大把高质量资料？一线教师？一线教研员？欢迎加入21世纪教育网教师合作团队！！！月薪过万不是梦！！